Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

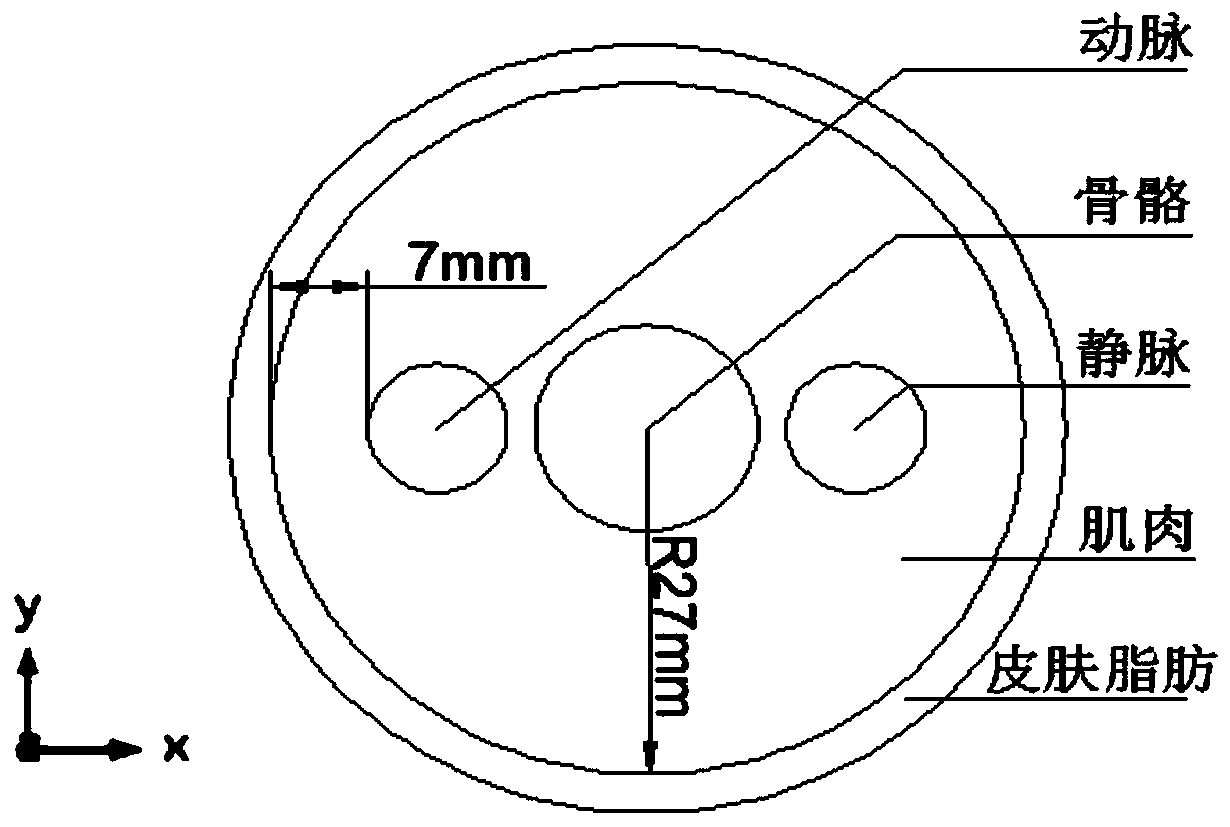
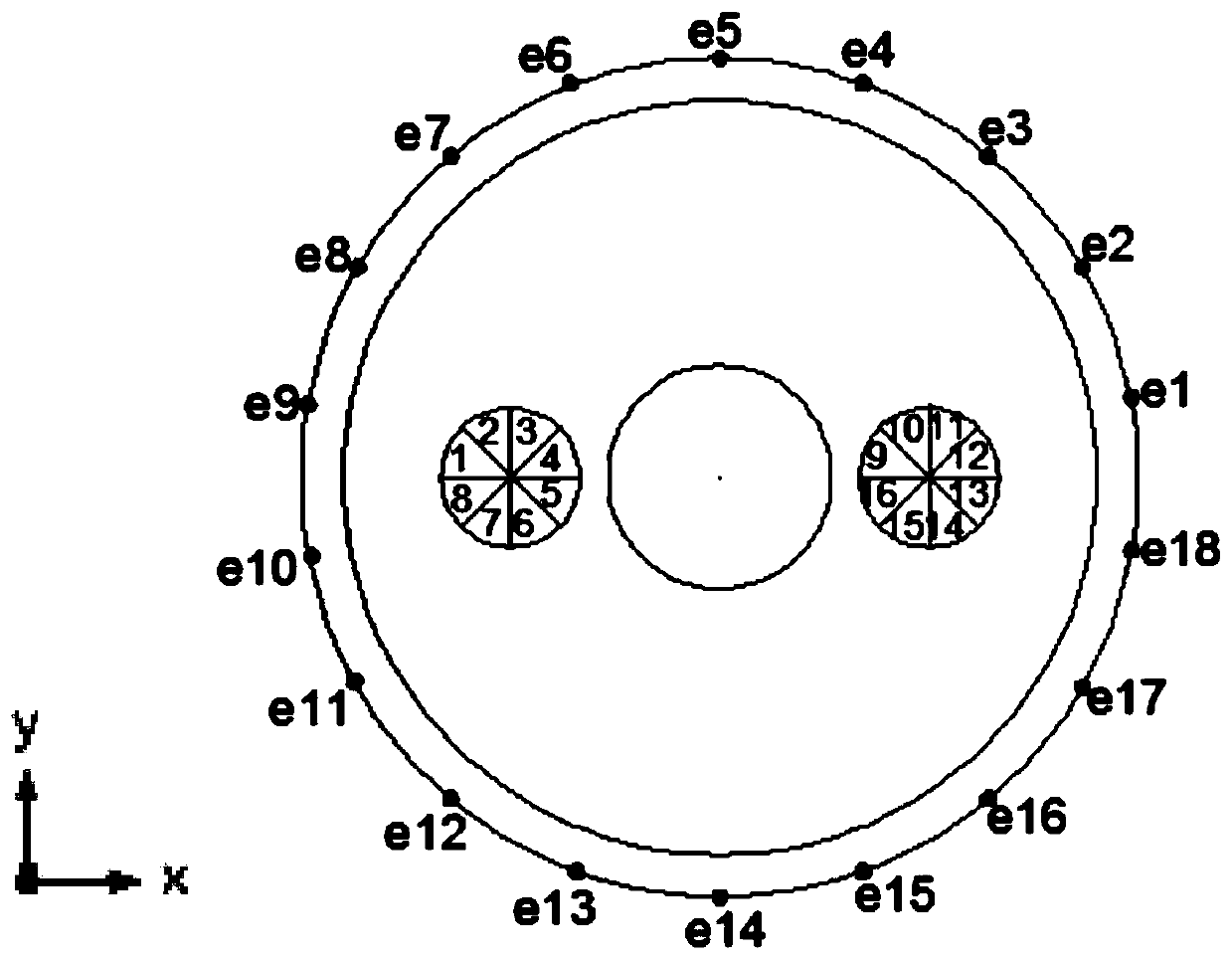
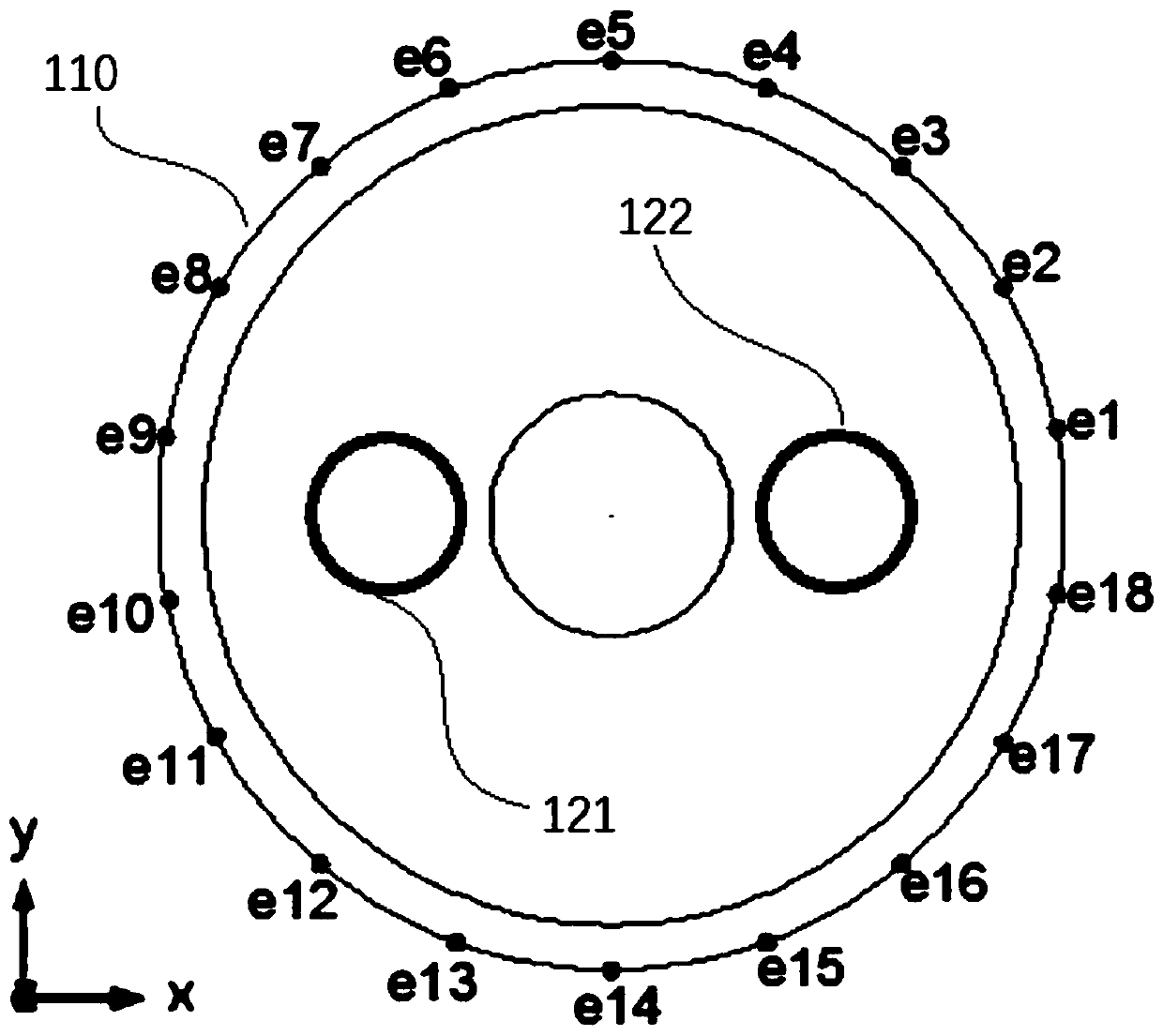
Flow velocity distribution reconstruction method for multi-electrode electromagnetic flowmeter

A technology of electromagnetic flowmeter and flow velocity distribution, which is applied in the direction of calculation, 3D modeling, design optimization/simulation, etc., can solve problems such as ill-posedness, and achieve the effect of improving accuracy

Pending Publication Date: 2020-05-12
HEBEI UNIVERSITY OF SCIENCE AND TECHNOLOGY
View PDF0 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0005] The present invention provides a multi-electrode electromagnetic flowmeter flow velocity distribution reconstruction method, which is used to solve the ill-posed problem existing in the multi-electrode electromagnetic flowmeter and the flow velocity distribution reconstruction method in the background technology after the measurement microelement increases

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Flow velocity distribution reconstruction method for multi-electrode electromagnetic flowmeter
  • Flow velocity distribution reconstruction method for multi-electrode electromagnetic flowmeter
  • Flow velocity distribution reconstruction method for multi-electrode electromagnetic flowmeter

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0087] This embodiment is a solution method using standard Tikhonov to realize step S40, and the difference from the comparative example is:

[0088] Step S42, determine its continuous regularization parameter λ.

[0089] Specifically, in this embodiment, the continuous regularization parameter λ can be obtained through the GCV method of formula (4-2). Such as Image 6 As shown, the abscissa is the continuous regularization parameter λ, and the ordinate is the solution G(λ) of formula (4-2) corresponding to the continuous regularization parameter λ, which determines the optimal continuous regularization parameter λ.

[0090] In an improved embodiment of this embodiment, it can also be obtained by the L curve method: Specifically, in this improved embodiment, it is obtained by the L function in the MATLAB regularization toolbox (version 4.1), for different regularization parameter plots its residual norm and the regularization norm x 2The two-dimensional graph between , si...

Embodiment 2

[0097] This embodiment is a solution method using TSVD_TIK to realize step S40, the difference from Embodiment 1 is:

[0098] Step S42: Determine its continuous regularization parameter λ and discrete regularization parameter k.

[0099] Specifically, in this embodiment, both the continuous regularization parameter λ and the discrete regularization parameter k can be obtained through the GCV method of formula (4-2).

[0100] In some improvements of this embodiment, in the embodiment, the continuous regularization parameter λ can also be calculated by the L-curve method as in the above-mentioned embodiment.

[0101] Step S43, solve by TSVD_TIK method.

[0102] This embodiment is based on the Tikhonov regularization method, that is, on the finite-dimensional space, based on the least squares criterion, the regularization matrix and the regularization parameter are introduced through formula (4-3), and the solution is constrained, Transform the problem into an optimization prob...

Embodiment 3

[0109] This embodiment is a solution method using F_TIK to realize step S40, the difference from Embodiment 2 is:

[0110] Step S42, determine its continuous regularization parameter λ.

[0111] Specifically, the process of obtaining the continuous regularization parameter λ in this embodiment may be the same as step S42 in the first embodiment or an improved embodiment of the first embodiment.

[0112] Step S43, solve by F_TIK method.

[0113] Compared with Embodiment 2, this embodiment is based on the Tikhonov regularization method, that is, in a finite-dimensional space, based on the least squares criterion, the regularization matrix and regularization parameters are introduced through formula (4-3) , constrain its solution, transform the problem into an optimization problem, but finally solve it by the F_TIK method.

[0114] Specifically, the solution of the calculation F_TIK method is transformed into

[0115]

[0116] In the formula, λ is the regularization paramet...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a flow velocity distribution reconstruction method for a multi-electrode electromagnetic flowmeter, belongs to the technical field of non-invasive measurement, and relates toa section detection device of a long cylinder type flow velocity field, which is used for measuring area section flow velocity distribution, and comprises the following steps: establishing a section model consistent with a measurement surface at a measurement electrode of a multi-electrode electromagnetic flowmeter, the measurement surface at least comprising one flow velocity field section; acquiring a regional weight function matrix, a regional area diagonal matrix and a speed reconstruction expression corresponding to the regional infinitesimal division mode of the flow velocity field section; acquiring an electrode pair induced voltage matrix of the measuring surface through the multi-electrode electromagnetic flowmeter; and solving and reconstructing a velocity matrix of the flow velocity field section through the electrode pair induced voltage matrix and the velocity reconstruction expression. The invention provides a method suitable for arranging measuring electrodes around oneor more measuring surfaces and measuring and reconstructing a flow velocity field passing through the measuring surfaces of a multi-electrode electromagnetic flowmeter.

Description

technical field [0001] The invention belongs to the technical field of non-invasive measurement, and relates to a cross-section detection device of a long tube-shaped flow velocity field, in particular to a method suitable for measuring blood flow velocity distribution in human blood vessels. Background technique [0002] Monitoring changes in blood flow rate can prevent and control major cardiovascular diseases that plague humans in advance, such as coronary artery stenosis and coronary heart disease. In view of the asymmetry of blood flow in mammals and the non-invasiveness of multi-electrode electromagnetic measurement methods, there have been beneficial attempts to apply multi-electrode electromagnetic measurement methods to the measurement of blood flow velocity in human limbs. Obtaining different string end voltages at the limb cross-section through multiple electrodes, and using the average flow velocity expression under any flow pattern to realize velocity distributi...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06F30/20G06T17/00
CPCG06T17/00
Inventor 吴学礼姚健赵宇洋甄然
Owner HEBEI UNIVERSITY OF SCIENCE AND TECHNOLOGY
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com