Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Digital signature method and system with security only depending on discrete logarithms

A digital signature and discrete logarithm technology, applied in the field of information security, can solve problems such as long signature data, and achieve the effects of short signature data, high efficiency, and low computational complexity

Active Publication Date: 2020-09-11
麦希科技(北京)有限公司
View PDF2 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Some digital signature algorithms require bit-by-bit operations, exponential operations or bilinear mapping operations, making the signature data output by the algorithm longer

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Digital signature method and system with security only depending on discrete logarithms
  • Digital signature method and system with security only depending on discrete logarithms
  • Digital signature method and system with security only depending on discrete logarithms

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

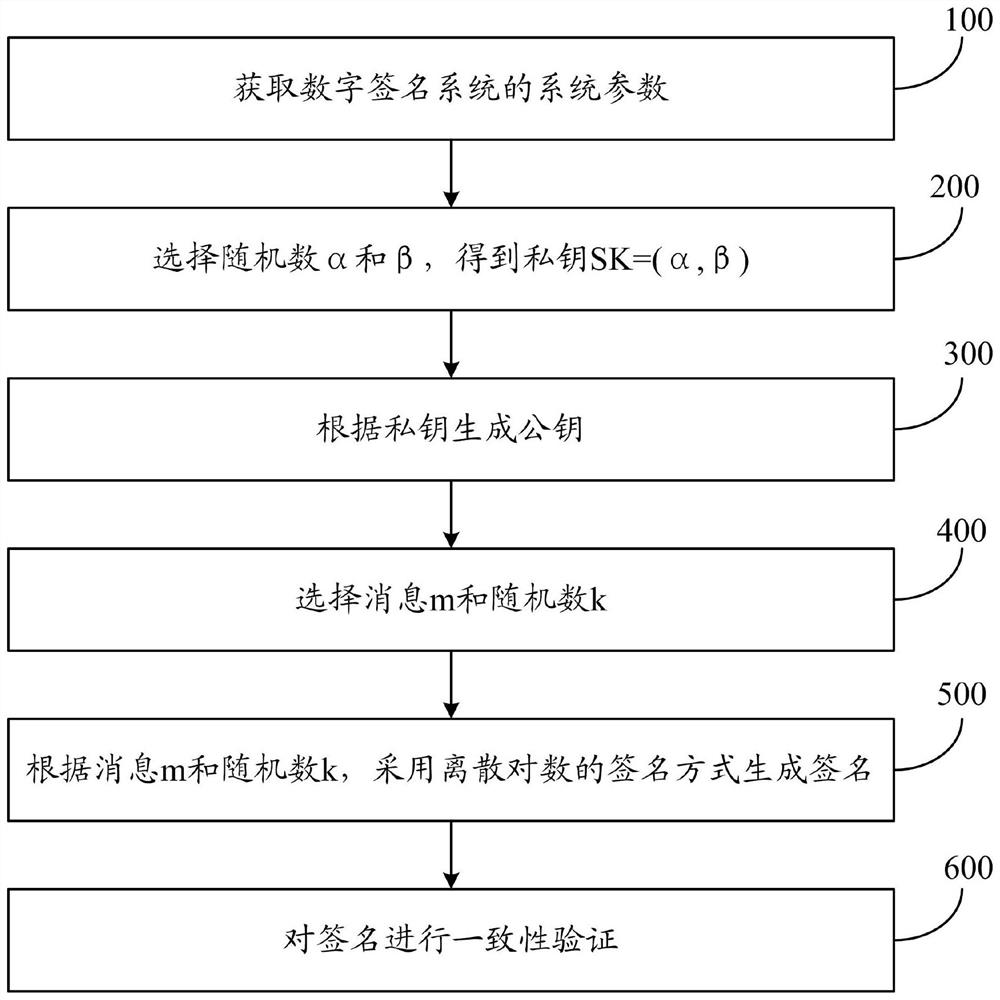
[0081] This embodiment is a digital signature method based on elliptic curve discrete logarithm, and the process is as follows:

[0082] System parameter generation: finite field is F q , the elliptic curve y 2 =x 3 +ax+b in the finite field F q The two parameters above are a, b. point group on elliptic curve The generator of is G, and its order is a large prime number n, where n>2 160 , the system parameters are:

[0083]

[0084] Key generation: choose a random number As private key SK=(α,β);

[0085] Calculated as follows

[0086]

[0087]

[0088] Then the public key is PK=(A, B).

[0089] Signature: choose message m ∈ Z n ,random number Using the formula (x 1 ,y 1 )=k·G to determine the new coordinate point (x 1 ,y 1 ), G is the coordinate point, after calculation with k, a new coordinate point (x 1 ,y 1 ).

[0090] According to the abscissa x of the new coordinate point 1 , using the formula σ 1 =x 1 modn calculates the first parameter σ...

Embodiment 2

[0103] This embodiment is a digital signature based on discrete logarithm, and the specific process is as follows:

[0104] System parameter generation: select a large prime number q,p, where q≥2 160 ,p≥2 1024 , and q|p-1. The generator of the cyclic group G is g, and its order is q, then the system parameters are SP=(G,g,q,p)

[0105] Key generation: choose a random number As the private key SK=(α,β), it is calculated as follows

[0106] A=g α mod p∈G

[0107] B=g β mod p∈G

[0108] Then the public key is PK=(A, B).

[0109] Signature: choose message m ∈ Z n ,random number calculate

[0110] X=g k mod p

[0111] σ 1 =X mod q

[0112] σ 2 =k -1 (α+m+β·σ 1 ) mod q

[0113] If σ 1 = 0 or σ 2 = 0, reselect the random number k and recalculate σ 1 ,σ 2 ;

[0114] If σ 1 ≠0 and σ 2 ≠0, then the signature is determined to be (σ 1 ,σ 2 ).

[0115] Verification: check σ 1 ,σ 2 Whether they all belong to [1,q-1], if not, the signature verification is rej...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to a digital signature method and system with security only depending on discrete logarithms. The method comprises the following steps: acquiring system parameters of a digital signature system; selecting random numbers alpha and beta to obtain a private key SK = (alpha, beta); generating a public key according to the private key; selecting a message m and a random number k,wherein m belongs to Zn, Zn is an integer set composed of 0-n-1, and R represents random selection; generating a signature in a discrete logarithm signature mode according to the message m and the random number k; and performing consistency verification on the signature. Collision attacks can be resisted, and the safety performance of the digital signature system is improved.

Description

technical field [0001] The invention relates to the field of information security, in particular to a digital signature method and system whose security only depends on discrete logarithms. Background technique [0002] Digital signature is a basic cryptographic primitive in cryptography, which has a wide range of applications, such as digital certificates, electronic currency transactions, etc. However, the current digital signature algorithm still has deficiencies in terms of security, computational complexity and signature length, for example: [0003] Security relies on hash functions. Before the existing digital signature algorithm signs the data, it needs to calculate the hash value of the data. This method makes the security of the signature algorithm limited to the security of the hash function. In other words, if the hash function is insecure, the signature algorithm is insecure. For example, in the internationally famous ECDSA algorithm, the signature process i...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): H04L9/08H04L9/32
CPCH04L9/0869H04L9/0825H04L9/3252
Inventor 赵峰何畅彬钟林
Owner 麦希科技(北京)有限公司
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com