Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Deep neural network quantification method based on elastic significant bits

A deep neural network and quantization method technology, applied in the field of deep neural network quantization based on elastic effective bits, can solve the problems of difficult step function, decreased precision, and reduced computational efficiency of quantized models, achieving efficient multiplication calculations and low precision loss , the effect of improving the overall efficiency

Active Publication Date: 2020-10-13
NANKAI UNIV
View PDF5 Cites 13 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

None of these distributions are suitable for the bell-shaped distribution, but in most cases, the DNN weights / activation values ​​are bell-shaped distributed, which shows that APoT cannot adapt to most DNN quantization, which will bring a large decrease in accuracy
figure 2 The displayed APoT is used to quantize the complex step function of the projection, which is difficult to implement with simple scaling and rounding functions, so its time complexity and space complexity have reached O(n), which will greatly The reduced computational efficiency of the quantized model

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Deep neural network quantification method based on elastic significant bits
  • Deep neural network quantification method based on elastic significant bits
  • Deep neural network quantification method based on elastic significant bits

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

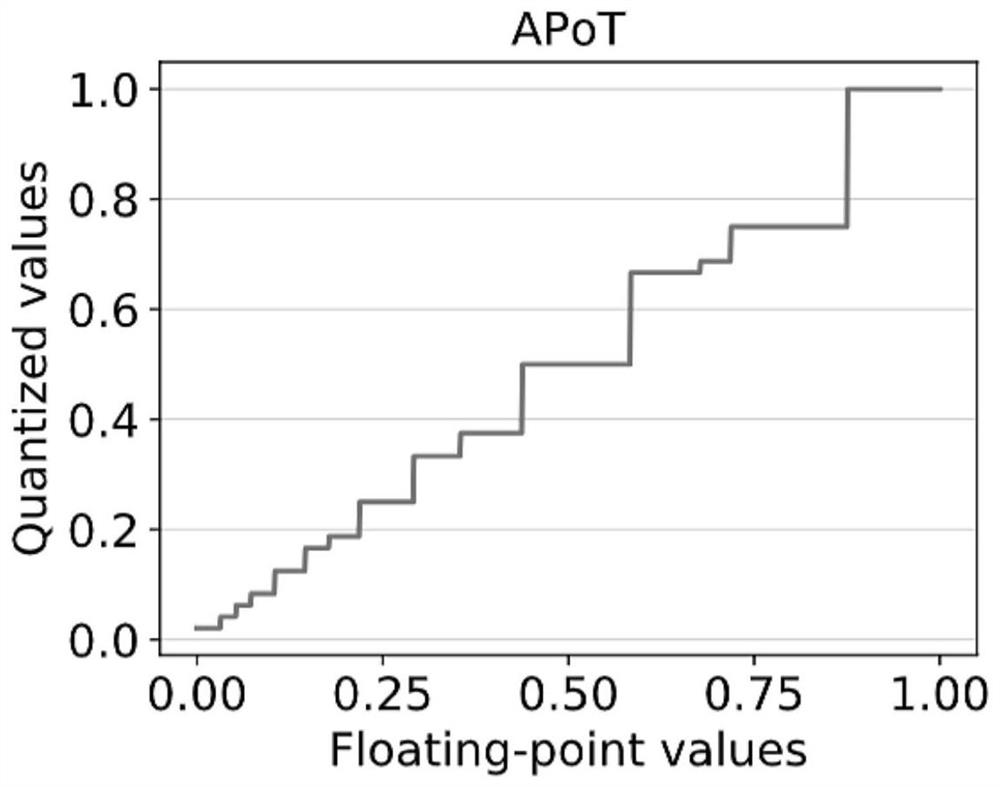
[0040] Embodiments of the present invention provide a deep neural network quantization method based on elastic effective digits, which quantizes fixed-point numbers or floating-point numbers into quantized values ​​with elastic effective digits, and discards redundant mantissa parts. The flexible significant bit is reserved from the most significant bit, and there are a limited number of significant bits.

[0041] For a given data v, from the position of its most significant bit, specify k+1 significant bits, expressed as follows:

[0042]

[0043] Among them, the part from (n-k) to n is the effective part reserved, and the part from 0(-∞) to (n-k-1) is the mantissa part that needs to be rounded; quantization of fixed-point or floating-point numbers:

[0044] P(v)=R(v>>n-k)<

[0045] Among them, >> and << are shifting operations, and R() is a rounding operation.

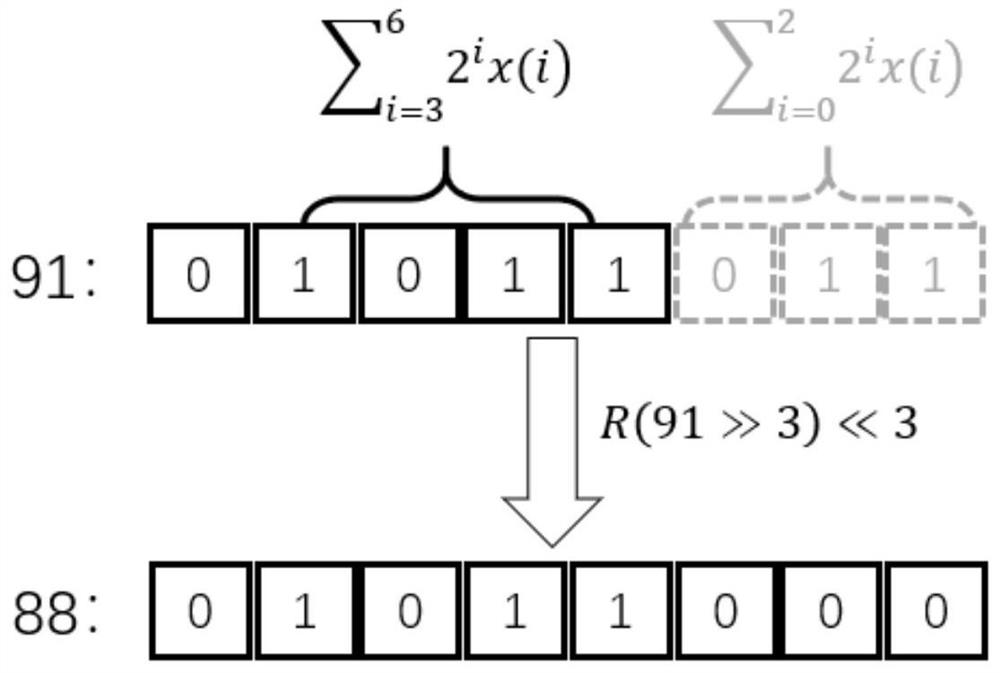
[0046] Such as image 3 As shown, in this embodiment, 91 is quantized, and the flexible valid bits are s...

Embodiment 2

[0049] Embodiments of the present invention provide a deep neural network quantization method based on elastic effective digits, which quantizes fixed-point numbers or floating-point numbers into quantized values ​​with elastic effective digits, and discards redundant mantissa parts. The flexible significant bit is reserved from the most significant bit, and there are a limited number of significant bits.

[0050] For a given data v, from the position of its most significant bit, specify k+1 significant bits, expressed as follows:

[0051]

[0052] Among them, the part from (n-k) to n is the effective part reserved, and the part from 0(-∞) to (n-k-1) is the mantissa part that needs to be rounded; quantization of fixed-point or floating-point numbers:

[0053] P(v)=R(v>>n-k)<

[0054] Among them, >> and << are shifting operations, and R() is a rounding operation.

[0055] Such as Figure 5 As shown, in this embodiment, 92 is quantized, and the flexible valid bits are ...

Embodiment 3

[0058] It is to quantitatively evaluate the distribution difference between the quantitative value and the original data by means of a feasible solution:

[0059] The quantization weight is W, which is sampled from random variables t~p(t), and the set of all quantization values ​​is Q, and the distribution difference function is defined as follows:

[0060]

[0061] s.t.S=(q-q l ,q+q u ]

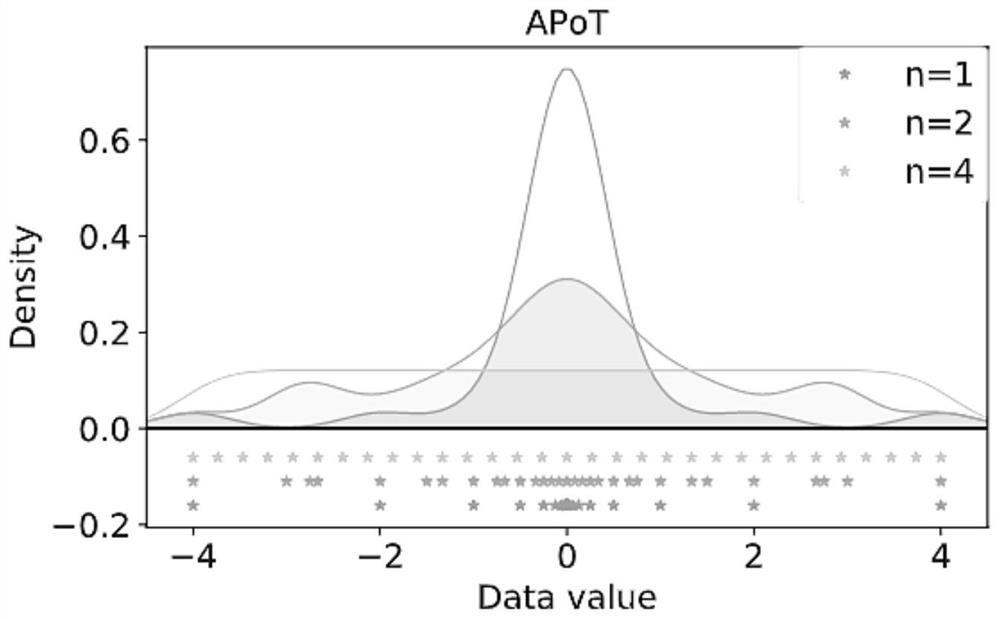
[0062] where (q-q l ,q+q u ] represents the range of continuous data that can be projected onto q-values, the range is centered at q, and q 1 and q u Indicates its floating range. Its solution diagram is as follows Figure 7 shown. Distribution differences can be used to evaluate optimal quantification at different elastic significands.

[0063] Input: There is a DNN weight w sampled from the standard normal distribution N(0, 1) f , it needs to be quantized to a low-precision value of 4 bits;

[0064] Output: the optimal effective number of digits, quantized weight w q .

[0...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides a deep neural network quantization method based on elastic significant bits. According to the method, a fixed point number or a floating point number is quantized into a quantized value with elastic significant bits, redundant mantissa parts are discarded, and the distribution difference between the quantized value and original data is quantitatively evaluated in a feasiblesolution mode. According to the invention, by using the quantized values with elastic significant bits, the distribution of the quantized values can cover a series of bell-shaped distribution from long tails to uniformity through different significant bits to adapt to weight / activation distribution of DNNs, so that low precision loss is ensured; multiplication calculation can be realized by multiple shift addition on hardware, so that the overall efficiency of the quantization model is improved; and the distribution difference function quantitatively estimates the quantization loss brought bydifferent quantization schemes, so that the optimal quantization scheme can be selected under different conditions, low quantization loss is achieved, and the precision of the quantization model is improved.

Description

technical field [0001] The invention belongs to the technical field of deep neural network compression, in particular to a deep neural network quantization method based on elastic valid bits. Background technique [0002] Deep Neural Networks (DNNs) quantization is an effective way to compress DNNs, which can significantly improve the computational efficiency of DNNs and enable the network to be deployed on edge computing platforms with limited resources. One of the most common ways to achieve quantization in DNNs is to project high-precision floating-point values ​​into low-precision quantized values. For example, DNNs with 32-bit floating point can achieve 32x model size compression by replacing weights with only one bit, and even reduce complex multiplication operations to simple bit operations on hardware. Therefore, in the case of fewer bit values, DNN quantization can significantly reduce the computational scale or memory footprint, thereby improving computational eff...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06N3/08G06N3/063
CPCG06N3/063G06N3/082
Inventor 龚成卢冶李涛
Owner NANKAI UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com