Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Posture smooth transition method and system

A technology of smooth transition and attitude, applied in the field of robotics, can solve the problem that the time derivative of the transition curve has no clear meaning.

Active Publication Date: 2021-02-12
HRG INT INST FOR RES & INNOVATION
View PDF6 Cites 4 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

This invention application uses B-splines with 5 control points to construct the attitude transition curve. The constructed attitude transition curve and the front and rear attitude interpolation curves have two-order geometric continuity at the junction, but the parameters of the transition curve have no clear meaning to the time derivative. , it is difficult to plan the trajectory according to the changing law of angular velocity

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Posture smooth transition method and system
  • Posture smooth transition method and system
  • Posture smooth transition method and system

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0085] This embodiment provides a detailed description of the gesture smooth transition method.

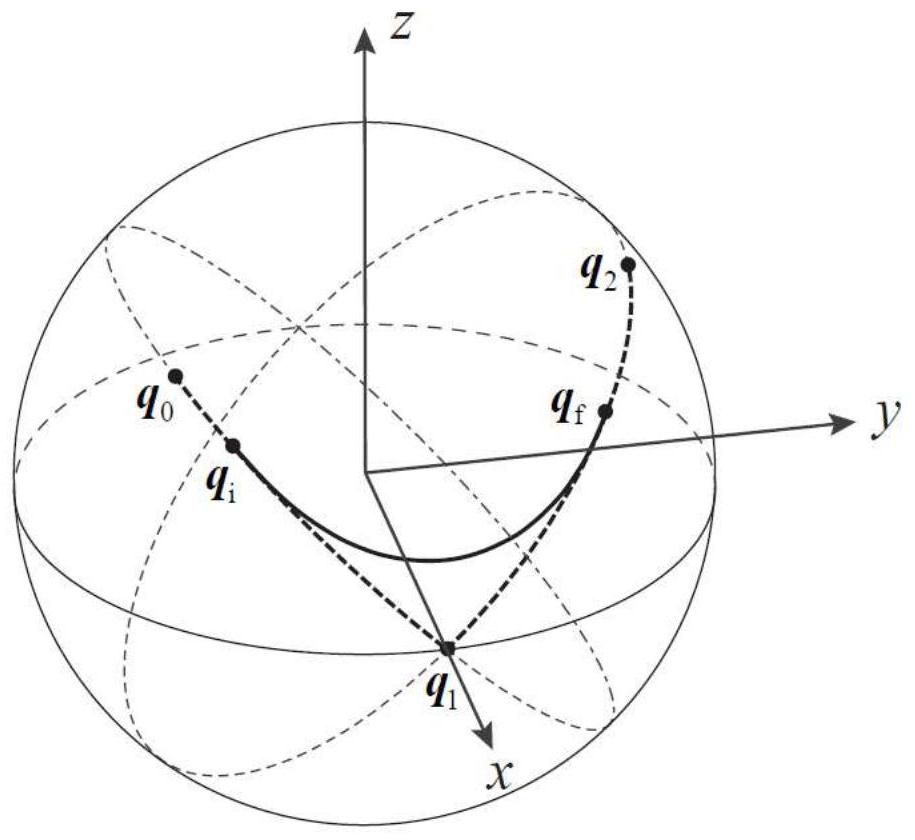
[0086] A method for attitude smooth transition, three attitudes q are known 0 ,q 1 ,q 2 , where by the pose q 0 to q 1 The axis of rotation is u 0 , the rotation angle is α 0 >0; by q 1 to q 2 The axis of rotation is u 1 , the rotation angle is α 1 >0; u 0 and u 1 The included angle is β, β≠0.

[0087] Select a reference coordinate system, and the coordinate vectors i, j, k of the reference system are determined by the following formula:

[0088]

[0089] In the reference frame, the axis of rotation u 0 , u 1 Expressed as

[0090]

[0091] The attitude is represented by the unit quaternion, according to the spherical linear interpolation, by q 0 to q 1 The interpolation curve of can be expressed by the following parametric equation:

[0092] q 01 (s)=p 01 (s)q 1 , s ∈ [0, 1]

[0093] s is a parameter and

[0094]

[0095] represented by pose q 1 to...

Embodiment 2

[0173] This embodiment provides when α 0 = 120°, α 1 =150°, α=90°, β=90°, q 0 = (1, (0, 0, 0)), the detailed description of the attitude transition curve is determined.

[0174] According to α and β, according to formula (4) to obtain

[0175]

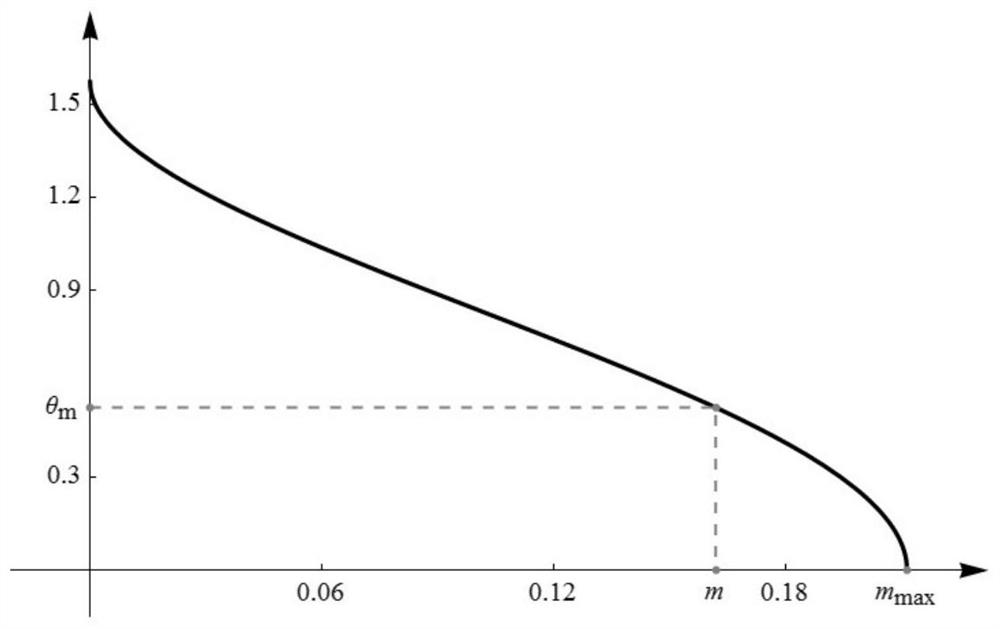
[0176] θ m =arcsin(sin45°cos45°)=30°

[0177] By formula (6) get

[0178]

[0179] By formula (9) get

[0180]

[0181] Using dichotomy, in the interval [0, m max ] to search for the root of m in formula (8), and get

[0182] m=0.161838

[0183] figure 1 For the right side of formula (8) in the interval [0, m max ] on the change graph, the vertical coordinate in the graph is θ m The abscissa value corresponding to the point is equal to m.

[0184] Calculated according to formula (6), formula (7) and formula (10)

[0185] n=0.265482, c ψ = 1.268094, σ = 2.587944

[0186] put m,n,c ψ , η, θ m Substituting the value of in turn into formula (5) and formula (3), we can get p 0 (s), p 1 (s) and p 2 The detailed e...

Embodiment 3

[0195] This embodiment provides an explanation of trajectory planning for the attitude transition curve in Embodiment 2 according to the change law of angular velocity.

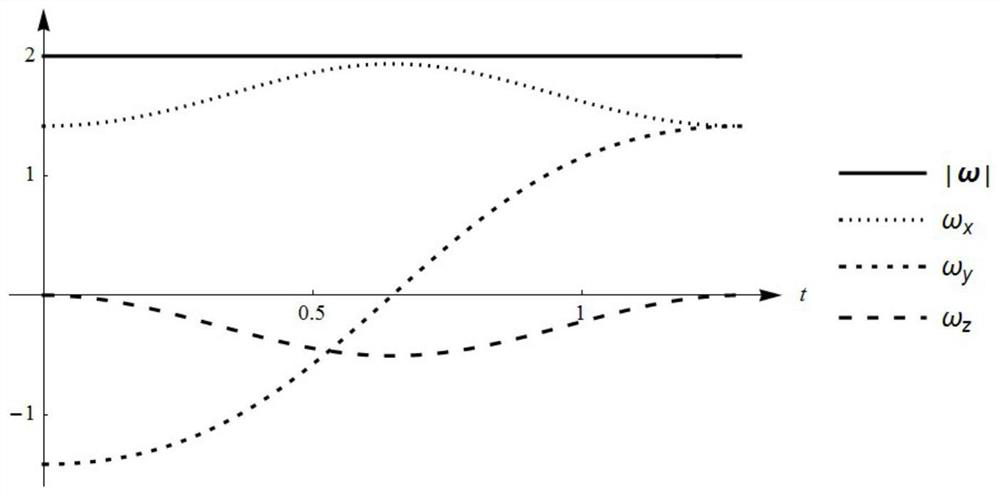
[0196] The attitude transition curve that obtains in embodiment 2 is carried out trajectory planning, promptly determines the variation law s (t) of the parameter s in the transition curve parametric equation about time. The change law of known angular velocity is: at the starting point q i and endpoint q f The magnitude of the angular velocity is 2, and by q i transition to q f The angular velocity is kept constant during the process.

[0197] Using the derivative of parameter s with respect to time is equal to the magnitude of angular velocity, we can get the change law of parameter s with respect to time, s(t) should be:

[0198] s(t)=2t, t∈[0,σ / 2]

[0199] After both q(s) and s(t) are determined, the change law of attitude over time can be obtained, image 3 It is the magnitude of the angular veloci...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides a posture smooth transition method. According to the method, constructed posture transition curve and front and rear posture interpolation curves have two-order geometric continuity at joints, so that an angular velocity can be smooth everywhere and an angular acceleration can be continuous everywhere; and in addition, a parameter-to-time derivative in a transition curve parameter equation is equal to the angular velocity, so that trajectory planning can be performed conveniently according to an angular velocity change rule.

Description

technical field [0001] The invention relates to the technical field of robots, in particular to a method and system for smooth transition of postures. Background technique [0002] The robot programming system provides several basic motion commands, such as linear motion, circular motion, etc. The robot executes motion instructions one by one, and the tool center point moves along the path defined by the instructions. If it is not set, the robot will have zero speed at the target point of each instruction. For some applications, in order to improve efficiency, it is hoped that the robot can keep moving between adjacent instructions, and the robot is allowed to deviate from the path within a certain range. A typical solution to this problem is to insert a transition path between the paths defined by adjacent instructions. In order to ensure smooth movement and avoid the impact of acceleration jumps on the machine body, the transition path and the front and rear path sectio...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): B25J9/16G06F17/15
CPCB25J9/1664G06F17/15
Inventor 王华郭庆洪吴自翔于振中李文兴
Owner HRG INT INST FOR RES & INNOVATION
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com