Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Ciphertext covariance matrix calculation method based on row coding

A technology of covariance matrix and calculation method, which is applied in calculation, computer security devices, complex mathematical operations, etc., can solve problems such as utilization and data exposure, and achieve the effect of ensuring privacy security and providing security protection

Active Publication Date: 2021-08-17
NO 30 INST OF CHINA ELECTRONIC TECH GRP CORP
View PDF7 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Solved the problem that in the plaintext domain environment, the data exposed during the calculation of the covariance matrix can be exploited by malicious parties

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Ciphertext covariance matrix calculation method based on row coding
  • Ciphertext covariance matrix calculation method based on row coding
  • Ciphertext covariance matrix calculation method based on row coding

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

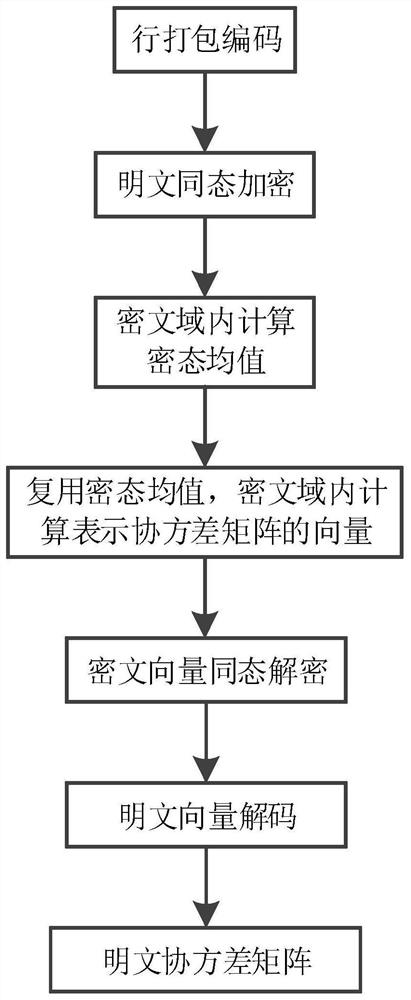
[0032] refer to figure 1 As shown, the invention discloses a method for calculating a ciphertext covariance matrix based on row coding.

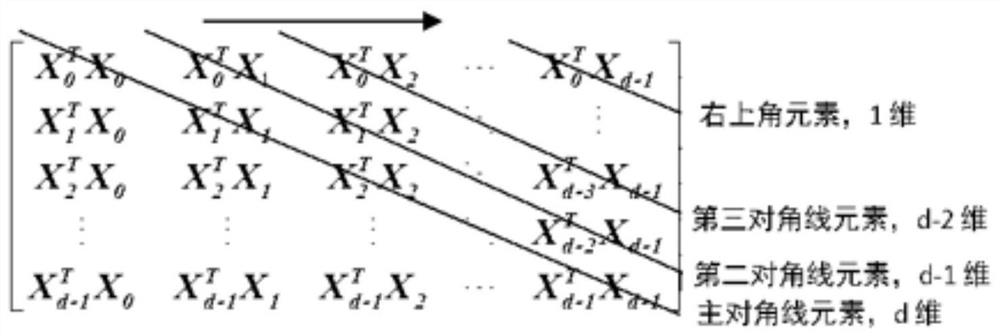
[0033] Let the data matrix X∈R n×d , containing n samples, each sample has d-dimensional features, x i,j Represents the j-th feature in the i-th sample.

[0034] in,

[0035] Covariance is generally used to describe the similarity between two random variables. To calculate the covariance matrix, each column of the data matrix X is regarded as a variable, and the covariance matrix is ​​used to describe the similar relationship between the variables in each column and other variables. In addition, (∑ X ) ij with (∑ x ) ji The meaning of the expression is the same, and the values ​​are also equal.

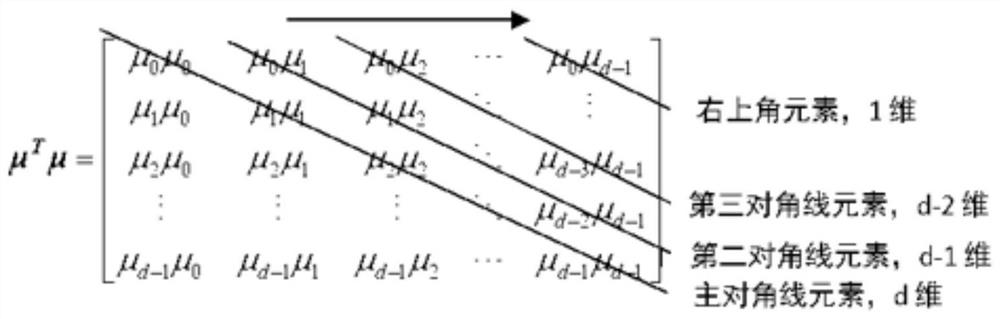
[0036] That is, the covariance matrix ∑ X is a symmetric matrix, and its calculation process is as follows:

[0037] Among them, μ represents the mean vector of the data matrix X, so that μ=[μ 0 ,μ 1 ,…,μ d-1 ], X=[X 0 ,X 1 ,...,...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a ciphertext covariance matrix calculation method based on row coding, which is used for completing efficient covariance matrix calculation of high-dimensional data in a ciphertext domain and ensuring the privacy security of original operation data. The problem that in a plaintext domain environment, data are exposed in the covariance matrix calculation process and then utilized by malicious parties is solved. In combination with a homomorphic encryption scheme, a covariance calculation algorithm is converted into a ciphertext domain, and the complexity of ciphertext covariance matrix calculation is controlled by optimizing the ciphertext calculation algorithm.

Description

technical field [0001] The invention belongs to the technical field of encryption, in particular to a method for calculating a ciphertext covariance matrix based on row coding. Background technique [0002] As a characteristic of multidimensional random variables, the covariance matrix is ​​widely used in mathematical models of statistics and machine learning to analyze the linear correlation between random variables. [0003] At present, the calculation of the covariance matrix of multivariate data is carried out in the plaintext domain, and its algorithm is relatively mature. The complexity of the algorithm is generally positively related to the data dimension and data volume. However, the plaintext domain needs to operate on the original data. The original data may contain some privacy-sensitive information. Obtaining the original data by a malicious party will also cause troubles to the data owner. At present, due to people's increasing demand for data privacy, it is ur...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F17/16G06F21/60G06F21/62
CPCG06F17/16G06F21/602G06F21/6245
Inventor 黄云帆汤殿华赵伟任娟尉小鹏
Owner NO 30 INST OF CHINA ELECTRONIC TECH GRP CORP
Features
  • Generate Ideas
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com