Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Self-adaptive new multi-extended target tracking method

A multi-extended target and extended target technology, which is applied in the field of self-adaptive new multi-extended target tracking, can solve the problem of poor multi-extended target tracking effect

Pending Publication Date: 2022-01-07
GUILIN UNIV OF ELECTRONIC TECH
View PDF0 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0003] The purpose of the present invention is to provide an adaptive nascent multi-extended target tracking method, aiming to solve the technical problem in the prior art that the detection probability and the position of the nascent target are both unknown and the multi-extended target tracking effect is poor

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Self-adaptive new multi-extended target tracking method
  • Self-adaptive new multi-extended target tracking method
  • Self-adaptive new multi-extended target tracking method

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

[0028] The following describes in detail the embodiments of the present invention, examples of which are illustrated in the accompanying drawings, wherein the same or similar reference numerals refer to the same or similar elements or elements having the same or similar functions throughout. The embodiments described below with reference to the accompanying drawings are exemplary, and are intended to explain the present invention and should not be construed as limiting the present invention.

[0029] In this application document, the following terms are used: 'std' means standard Poisson-Do Bernoulli mixing filtering based on fixed nascent distribution, 'tb' means filtering based on adaptive nascent distribution, 'gbs' means Gibb Sampling, 'BGGIW' means filtering based on unknown detection probability, 'ture value' means actual but unknown detection probability, 'PHD' means probability hypothesis density filtering.

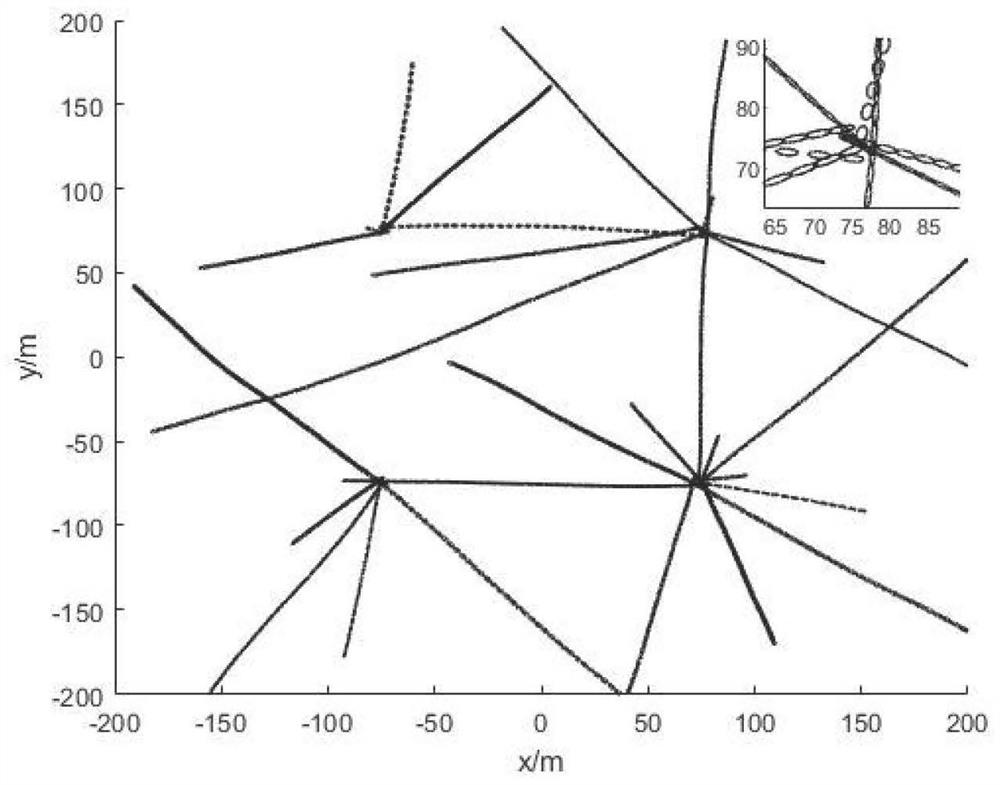
[0030] see figure 1 , the present invention proposes an ada...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a self-adaptive new multi-extended target tracking method, which solves the tracking problem of unknown new target positions through a new measurement-driven self-adaptive new distribution method, and comprises the following steps of firstly, representing the correlation between measurement and a target through likelihood and proximity, generating a new target near a measurement value by using the correlation, describing an unknown detection probability through beta distribution, describing an extended target state through gamma Gaussian inverse Weichart distribution, modeling the target state and the detection probability as an augmented state, and realizing the tracking problem of multiple extended targets under the unknown detection probability. In addition, in each iteration, the corrected PMBM filtering density is cut off through the Gibbs sampler, a positive 1-1 vector with a high weight is obtained, the efficiency of the filter is improved under the condition that the precision is not lost, and the technical problem that in the prior art, the multi-extension target tracking effect with the unknown detection probability and the unknown new target position is poor is solved.

Description

technical field [0001] The invention relates to the technical field of detection and tracking, in particular to an adaptive new multi-expansion target tracking method. Background technique [0002] In the existing multi-target tracking methods, most filters based on random finite sets (RFS), such as standard PMBM conjugate priors, assume that the detection probability and target new location are estimated from offline training data, that is, both is known prior information, but it is worth noting that this knowledge is uncertain in practical situations, and the research on multi-extended targets, adaptive target nascent algorithms, and PMBM conjugate priors under unknown detection probability has not been done yet. accomplish. SUMMARY OF THE INVENTION [0003] The purpose of the present invention is to provide an adaptive new multi-expansion target tracking method, which aims to solve the technical problem of poor multi-expansion target tracking effect in the prior art wh...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G01S13/66G01S13/72G01S7/41
CPCG01S13/66G01S13/726G01S7/411
Inventor 吴孙勇周于松谢芸薛秋条孙希延蔡如华纪元法符强严素清邓洪高
Owner GUILIN UNIV OF ELECTRONIC TECH
Features
  • Generate Ideas
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com