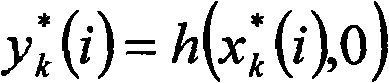Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Particle filtering resampling method suitable for non-linear probabilistic system posture

A non-linear random and system state technology, applied in the field of filtering, can solve the problems of poor state filtering accuracy, achieve the effect of improving filtering accuracy and overcoming poor filtering accuracy

Inactive Publication Date: 2009-01-07
HARBIN INST OF TECH
View PDF0 Cites 16 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0006] In order to solve the problem that the existing particle filter method filters the nonlinear system state, the particle swarm obtained by resampling is not completely gathered near the real system state because the observation likelihood function of the system state variable has a bimodal characteristic. To solve the problem of poor accuracy of state filtering, a particle filter resampling method suitable for the state of nonlinear stochastic systems is provided

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Particle filtering resampling method suitable for non-linear probabilistic system posture
  • Particle filtering resampling method suitable for non-linear probabilistic system posture
  • Particle filtering resampling method suitable for non-linear probabilistic system posture

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

[0034] Embodiment 1: The particle filter resampling method applicable to the state of nonlinear stochastic system in this embodiment will be described in detail below.

[0035] The state-space model of the nonlinear stochastic system is as follows:

[0036] x k =f(x k-1 , u k-1 )(system model) (1)

[0037] the y k =h(x k , v k )(observation equation) (2)

[0038] Among them, f(.) and h(.) are known nonlinear functions, u k and v k are the system noise and observation noise with known probability density function, x k is the system state at time k, y k is k time x k observation value;

[0039] Order y k Represents the observed value of the real state of the system at time k, {x k (i): i=1,...,N} represents the state sample set at time k, {x ＊ k (i): i=1,...,N} represents from {x k (i): The set of state samples obtained by resampling in i=1,...,N}, {x' k (i): i=1,...,N} represents a set of state samples, where

[0040] x' k (i)=f(x k-1 (i), 0), i=1, 2, .., N...

specific Embodiment approach 2

[0068] Embodiment 2: The difference between this embodiment and Embodiment 1 is that in step 2, the Pearson correlation coefficient function between two vectors or the angle function between two vectors is used as a function to measure the similarity of two vectors. When using the Pearson correlation coefficient function, the value range of s(i) is -1≤s(i)≤1, and when using the angle function, the value range of s(i) is 0≤s(i)≤π .

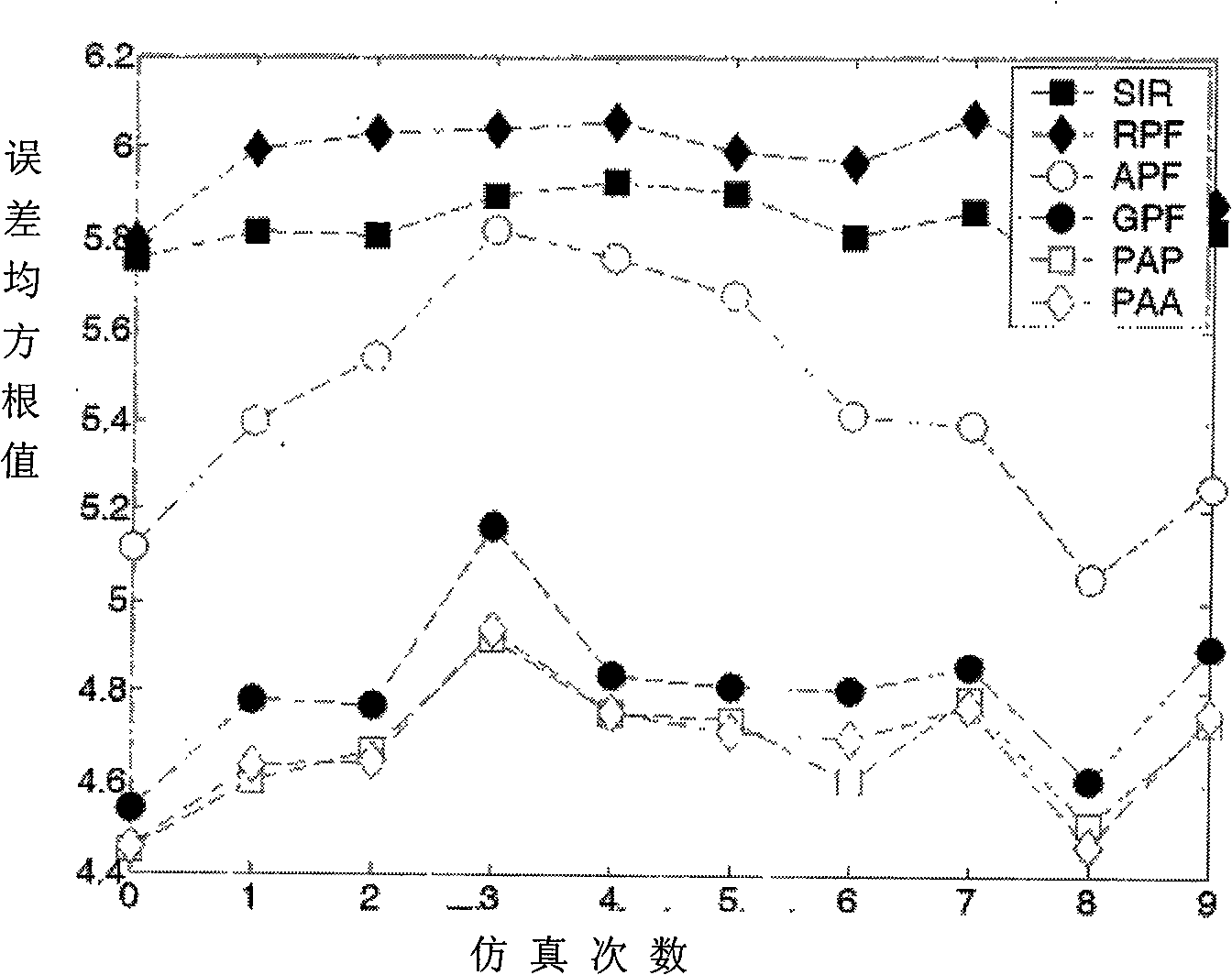
[0069] When this method is applied to the following representative nonlinear systems with bimodal characteristics of the observation likelihood function, the system state filtering accuracy is better than that of SIR, APF, RPF and GPF algorithms.

[0070] x k = x k - 1 2 + 25 x k - ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to a particle filter resampling method which is applied to a nonlinear stochastic system state. The invention relates to a filtering method, in particular to a particle filter resampling method for estimating the nonlinear stochastic system state. The invention aims at solving the problem that the filtering precision of the state is poorer as the observation and likelihood function of the system state has double-humped characteristic when the nonlinear stochastic system state is filtered. In the resampling method, the similarity degree of the observation vector of the particles and the observation vector of the system state is utilized, so as to regulate the weight of the particles that are involved in the resampling. The invention is applied to the state filtering problem of the common nonlinear stochastic system, when the observation and likelihood function of the system state has the double-humped characteristic, the method can improve the filtering precision of a particle filter to the nonlinear stochastic system state.

Description

technical field [0001] The invention relates to a filtering method, in particular to a particle filter resampling method for nonlinear random system state estimation. Background technique [0002] The state estimation problem of nonlinear stochastic system widely exists in signal processing and related fields. Despite nearly half a century of development, state filtering methods for nonlinear stochastic systems are still relatively immature. On the one hand, this is caused by the complexity and diversity of nonlinear stochastic systems; on the other hand, due to the existence of various random noises in nonlinear stochastic systems, state filtering is more difficult and affects the accuracy of state filtering. rate, which brings great difficulties to nonlinear stochastic system state filtering. Since the 1980s, nonlinear stochastic system state filtering methods have received more and more attention, among which the extended Kalman filter is the most commonly used. Since ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06K9/00
Inventor 彭喜元梁军彭宇乔立岩
Owner HARBIN INST OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com