Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Photovoltaic cell output characteristic modeling method

A photovoltaic cell and output characteristic technology, applied in the direction of electrical digital data processing, special data processing applications, instruments, etc., can solve problems such as large data and inaccurate photovoltaic cell models

Inactive Publication Date: 2013-03-27
NORTH CHINA ELECTRIC POWER UNIV (BAODING)
View PDF3 Cites 29 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0007] Aiming at the problems mentioned in the background technology that the existing photovoltaic cell model is inaccurate, too much data is required in the parameter calculation process, etc., the present invention proposes a photovoltaic cell output characteristic modeling method

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Photovoltaic cell output characteristic modeling method
  • Photovoltaic cell output characteristic modeling method
  • Photovoltaic cell output characteristic modeling method

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

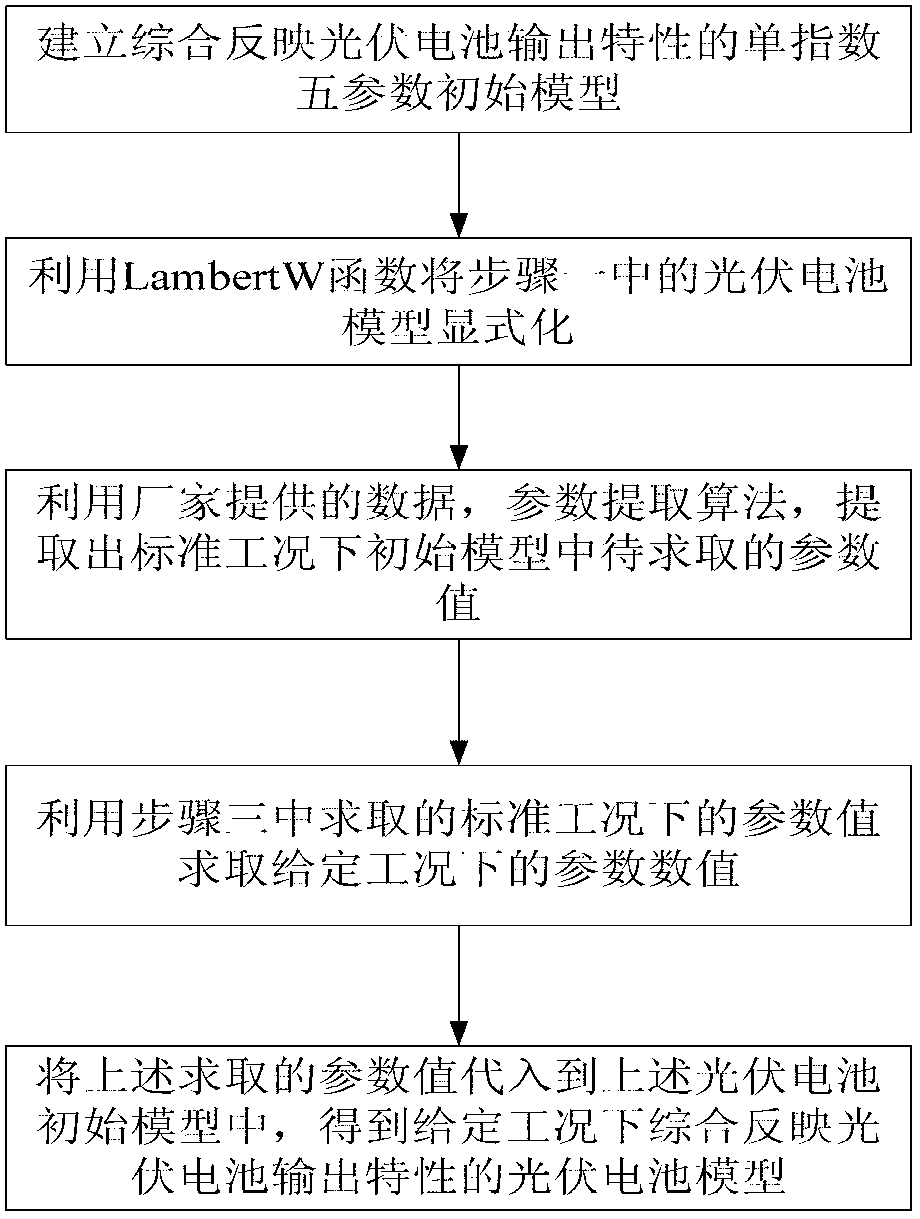
[0069] The preferred embodiments will be described in detail below in conjunction with the accompanying drawings. It should be emphasized that the following description is only exemplary and not intended to limit the scope of the invention and its application.

[0070] The specific steps of the modeling method are:

[0071] Step 1: Establish a single exponential 5-parameter initial model that comprehensively reflects the output characteristics of photovoltaic cells, wherein the 5 parameters in the above initial model are all values ​​to be obtained.

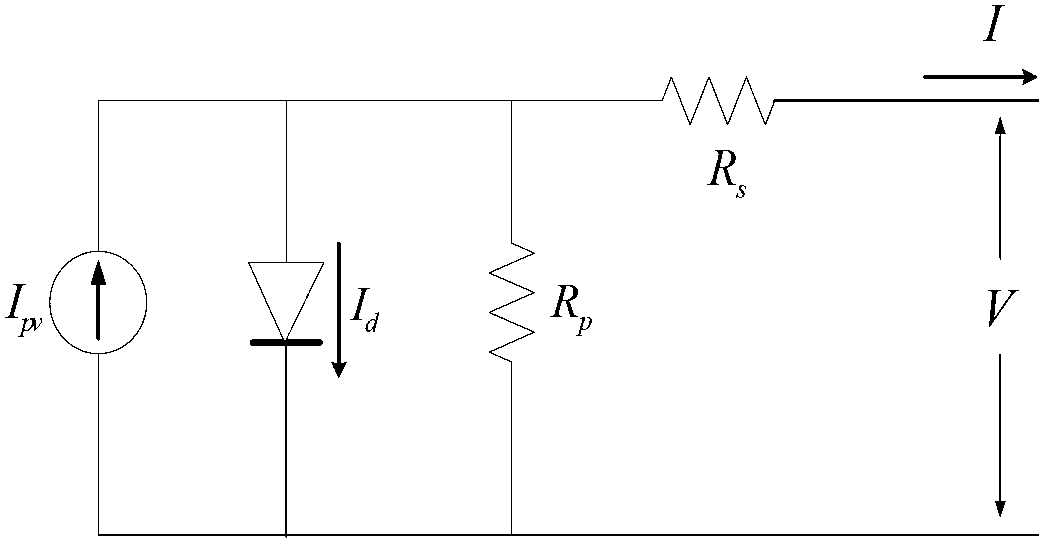
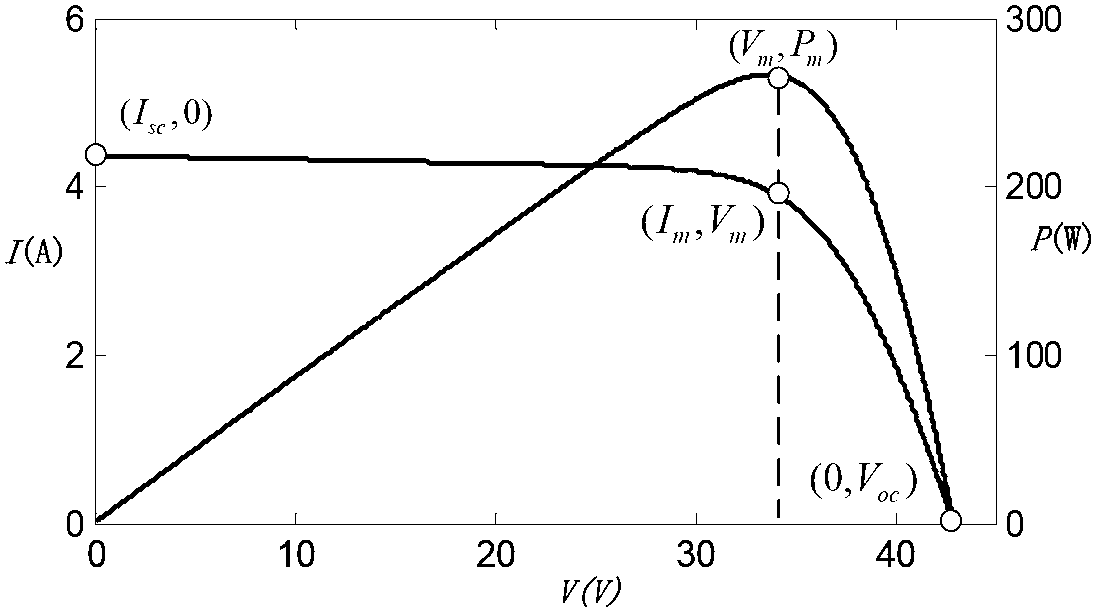
[0072] The equivalent circuit of a single exponential 5-parameter model of a photovoltaic cell is as figure 2 shown, according to figure 2 Available:

[0073] I = I pv - I 0 [ exp ( V + R s ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a photovoltaic cell output characteristic modeling method in the technical field of photovoltaic power generation. According to the technical scheme, the method comprises the following the steps of: establishing a single exponential parameter initial model which comprehensively reflects photovoltaic cell output characteristics; enabling the single exponential parameter initial model to be explicit by utilizing a Lambert W function so as to obtain a photovoltaic cell explicit model; calculating a to-be-calculated parameter value in the initial model under a standard working condition by utilizing data provided by manufacturers and a parameter calculating algorithm; and calculating a parameter value under a given working condition by utilizing the parameter value under the standard working condition and a parameter transformation algorithm; and substituting the calculated parameter value into the photovoltaic cell explicit model, thereby obtaining the photovoltaic cell model which comprehensively reflects photovoltaic cell output characteristics under the given working condition. The photovoltaic cell output characteristic modeling method provided by the invention has the beneficial benefits that the established photovoltaic cell model is accurate; data of manufacturers are only utilized during the parameter calculating process, and the parameter calculating algorithm is simple, and is wide in application range; and the explicit model is simple and convenient to use.

Description

technical field [0001] The invention belongs to the technical field of photovoltaic power generation, and in particular relates to a modeling method for photovoltaic cell output characteristics. Background technique [0002] With the increasing scarcity of energy, the development and utilization of renewable energy is imminent. Solar energy, as one of clean and renewable energy sources with large-scale development prospects, has attracted widespread attention for grid-connected power generation. [0003] Photovoltaic grid-connected power generation refers to the process in which the photovoltaic cell array converts solar energy into DC power, and the DC power is converted into AC power with the same frequency and phase as the grid through the inverter and fed into the grid. Since the accuracy of photovoltaic cell modeling and the difficulty of its realization affect the subsequent research and development of a series of technologies, such as maximum power tracking control, ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F19/00
Inventor 徐永海孔祥雨陶顺曾雅文肖湘宁
Owner NORTH CHINA ELECTRIC POWER UNIV (BAODING)
Features
  • Generate Ideas
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com