[0042] The technical solution of the present invention will be described in detail below in conjunction with the drawings:
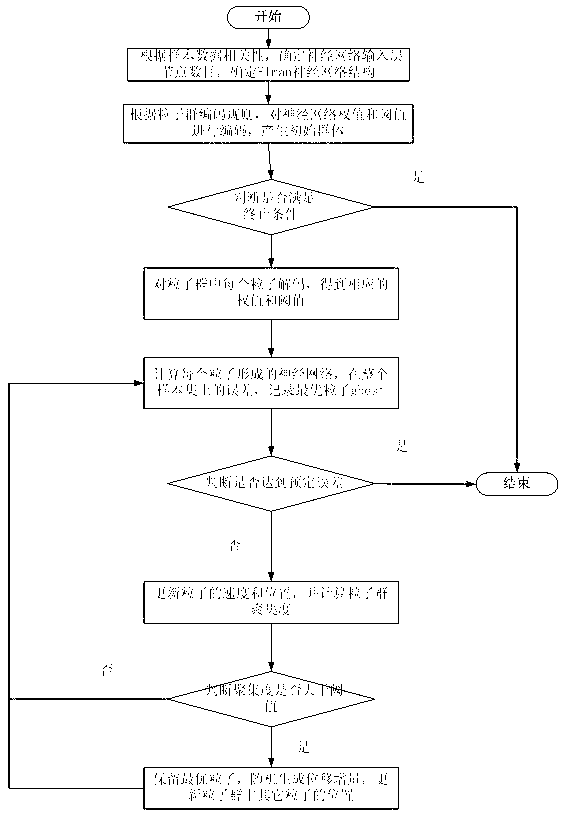
[0043] The present invention improves the particle swarm optimization algorithm and proposes a particle adjustment method based on the distribution of particle swarms. The main idea is to improve the particle swarm optimization algorithm in the existing particle swarm optimization neural network. In the process, when the particle swarm is densely distributed, add a random position increment to break up the particles, thereby jumping out of the local optimal solution.
[0044] In order to facilitate the public to understand the technical solution of the present invention, the following takes the PSO-Elman neural network prediction model as an example for detailed description.
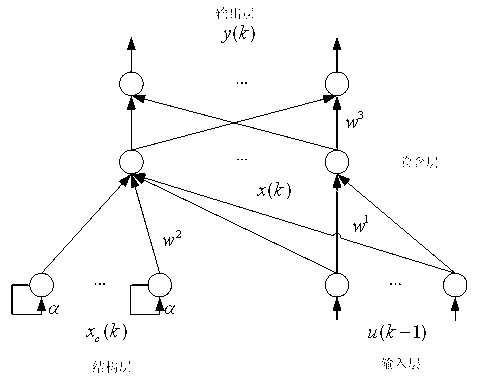
[0045] Such as figure 1 As shown, the Elman neural network structure includes four layers: input layer, hidden layer, structure layer, and output layer. Elman neural network feeds back the output of the hidden layer of the feedforward network model to a structure layer, including the structure layer and the hidden layer The number of units is the same. The function of the structure layer is to act as a delay operator of the neural network, so that it can memorize the output value of the hidden layer unit at the previous time, making it more sensitive to the data of the historical state. Suppose the input layer of the network has m nodes, the hidden layer and the structured layer have n nodes, and the output layer y(k) has r nodes, then the input layer of the network is an m-dimensional vector, and the hidden layer and structure layer are n-dimensional vector, the output layer is r-dimensional vector, connected with weight w 1 Is m×n dimensional matrix, w 2 Is an n×n dimensional matrix, w 3 Is an n×r-dimensional matrix, the mathematical model of the Elman network is:
[0046] x(k)=f(w 1 x c (k)+w 2 u(k-1)) (1)
[0047] x c (k)=x(k-1)+αx c (k-1) (2)
[0048] y(k)=g(w 3 x(k)) (3)
[0049] Where w 1 ∈R m×n , W 2 ∈R n×n , W 3 ∈R r×n These are the connection weight matrix from the input layer to the hidden layer, the structure layer to the hidden layer, and the hidden layer to the output layer; u(k-1) is the input vector of the input layer, and x(k) is the input layer Output vector, x c (k) is the input vector of the structure layer, y(k) is the output vector of the output layer; f(.) and g(.) are the excitation functions of the hidden layer unit and the output layer unit, and are generally sigmoid functions, namely α is the structural layer x c (k) The corresponding self-feedback factor.
[0050] The number of nodes (neurons) in each layer of the Elman neural network can be determined based on experience or various existing methods. In order to improve the prediction accuracy, the present invention uses the correlation of samples to determine the number of input layer nodes, as follows:
[0051] Suppose the total number of samples in the training sample set is P, and each sample is a time series X composed of t continuous historical data t ={x 1 ,x 2 ,...,x t }, for each sample, use the following formula to calculate the sample divided by x t Each historical data other than x i With x t The correlation between ρ i , I=1,2,…,t-1:
[0052] ρ k = Cov ( x t , x t - k ) Var ( x t ) Var ( x t - k ) ,
[0053] Where ρ k Means x t Historical data x at intervals of k sampling periods t-k With x t The correlation degree of k=1,2,...,t-1; Used to measure x t The degree of dispersion of the mean μ of the time series; Cov(x t ,x t-k )=E[(x t -μ)(x t-k -μ)], Cov(x t ,x t-k ) Means x t With x t-k Covariance; from x t-1 Start to count forward the number of historical data whose correlation degree is continuously greater than 0. From x t-1 Start to count forward the number of historical data with continuous correlation greater than 0 is m i;
[0054] Then the number m of input layer nodes of Elman neural network is obtained by the following formula:
[0055] m = 1 P X i = 1 P m i .
[0056] After determining the structure of the neural network, use the particle swarm algorithm to optimize the connection weights and thresholds of the neural network according to the training samples, which specifically includes the following steps:
[0057] Step 1. Perform particle coding on the connection weight and threshold to be optimized, and determine the particle swarm size, particle position and velocity, learning factor and inertia weight, where the dimension of each particle is the connection weight and threshold to be optimized The total number of.
[0058] The elements of the particles in the particle swarm are the self-feedback factor α and the weight of the Elman neural network. The particle coding format is as attached figure 2 As shown, the elements of particle X include sub-feedback factor α and neural network weights among them, They are an arrangement of the elements in the weight matrix expanded by row vectors.
[0059] Step 2. Initialize the population: randomly generate N particles of length L, and the particle population set is denoted as A.
[0060] Step 3. Iterative update:
[0061] Step 301: Calculate the fitness of each particle in the current particle swarm. The fitness function used in the present invention is the mean square error of the neural network:
[0062] Ft = 1 K X i = 1 K ( y ^ i - y i ) 2 - - - ( 6 )
[0063] Where K is the total number of training samples, Is the actual output of the neural network, y i Is the expected output of the neural network.
[0064] Step 302: Update the current individual extreme value pbest of each particle and the global optimal extreme value gbest of the particle population.
[0065] If according to the standard particle swarm optimization algorithm, the current individual extreme value pbest of each particle and the global optimal extreme value gbest of the particle swarm are obtained, the speed and position of the particles should be updated, as follows:
[0066] In the n-dimensional target search space, X i =(x i1 ,x i2 ,...,x in ) Is the current position of particle i, V i =(v i1 ,v i2 ,...,v in ) Is the current flying speed of particle i, P i =(p i1 ,p i2 ,...,p in ) Is the individual extreme value of particle i, P g (t)=(p g1 ,p g2 ,...,p gn ) Is the best position experienced by all particles in the group, that is, the global extremum. For the kth iteration, each particle is updated according to formula (7) and formula (8);
[0067] v ij (t+1)=wv ij (t)+c 1 r 1 (p ij (t)-x ij (t))+c 2 r 2 (p gj (t)-x ij (t)) (7)
[0068] x ij (t+1)=x ij (t)+v ij (t+1) (8)
[0069] In the formula, i represents the particle, j represents the j-th dimension of the particle, and w is the weighting coefficient, which is used to control the degree of influence of the historical speed on the current speed. Generally, the value is between [0.1, 0.9], c 1 , C 2 Is the learning factor, usually the value is 2, r 1 , R 2 It is a random number uniformly distributed on [0,1].
[0070] It can be seen from the speed update equation (7) that the speed update is divided into three parts. The first part is the initial speed. In the basic PSO algorithm, the initial speed is limited to a range, which is added in some later improved algorithms. Various deformation inertia factors adjust the global and local search capabilities of the algorithm to improve the convergence speed. It is the cognitive part. Obviously, this part is related to the particle itself. It records the influence of the particle's own motion on the subsequent speed. The third part is the social part. The movement of other particles in the group affects the particles. If only its own particles are updated, the algorithm is that many particles run independently, the workload of finding the optimal solution increases and the performance deteriorates. Similarly, if you only adjust your movement according to the group's situation, you may fall into a local optimum. Therefore, only reasonable use of the particle's own experience and group experience can the optimal solution be found quickly and accurately.
[0071] From the update method of speed and position in the above PSO algorithm, it can be seen that in each iteration process, the particles in the particle swarm are constantly approaching the optimal particle to the global optimal solution, and more and more particles will gather into the group. Losing their own speed, becoming more and more inactive, difficult to find the global optimal solution, and thus appear premature. In order to avoid this situation, the present invention proposes a particle adjustment method based on particle swarm distribution. The main idea is to add a random position increment to break up the particles when the particle swarm is densely distributed during each iteration. Thereby jumping out of the local optimal solution.
[0072] In order to calculate the distribution of particles in the particle swarm during each iteration, the present invention proposes the concept of aggregation. For the kth iteration, first calculate the distance between the i-th particle in the population and the global optimal particle as Let n be the number of particles in the particle swarm, and count d in the particle swarm i k ≤r k The number of particles is Nearnum k , Then the aggregation degree of the particle swarm is:
[0073] R k = Nearnum k n - - - ( 9 )
[0074] In each iteration, if R k η, the particles with the best fitness are retained, n-1 displacement increments are randomly generated, and the n-1 displacement increments are used to update the positions of n-1 particles other than the global optimal particle. That is, the distance between the n-1 particles and the global optimal particle plus a randomly generated displacement increment is used as the updated position of the particle; the range of the displacement increment is Among them, η is the aggregation degree threshold, MaxSet is the modulus of the maximum solution set, r k Is the neighborhood radius of the optimal particle in the kth iteration. Since the random displacement increment is half of the modulus of the maximum solution set, the radius of the neighborhood of the optimal particle is from Decrease, the calculation method is as formula (10):
[0075] r k = 1 2 X ( 1 - k Maxiter ) X MaxSet - - - ( 10 )
[0076] Among them, Maxiter represents the maximum number of iterations, and MaxSet is the modulus of the maximum solution set. It can be seen from equation (10) that the radius of the neighborhood decreases as the number of iterations increases. At the beginning of the operation, the radius of the neighborhood is larger, which can prevent particles from passing Fast aggregation causes the algorithm to converge to the local optimal solution prematurely, ensuring the early diversity of the particle swarm. In the later stage of the operation, the neighborhood radius is smaller, which is conducive to the convergence of the algorithm, preventing the algorithm from failing to converge, and ensuring the convergence of the algorithm.
[0077] The specific implementation of the particle adjustment method based on particle swarm distribution proposed in the present invention is to perform the operation described in step 303 before updating the velocity and position of the particles according to the existing method.
[0078] Step 303: Calculate the aggregation degree of the current particle swarm, and if the aggregation degree is greater than the preset aggregation degree threshold, keep the globally optimal particles and use the randomly generated n-1 ranges as Update the position of the other n-1 particles except the globally optimal particle by the displacement increment; where n is the total number of particles in the particle swarm, Maxset is the modulus of the maximum solution set; the current k-th iteration of the particle Cluster aggregation R k , Calculated according to the following method:
[0079] R k = Nearnum k n ,
[0080] In the formula, Nearnum k Is that the distance between the current particle swarm and the global optimal particle is less than r k The total number of particles; r k Is the neighborhood radius of the global optimal particle, calculated according to the following formula:
[0081] r k = 1 2 X ( 1 - k Maxiter ) X MaxSet ,
[0082] Among them, Maxiter is the maximum number of iterations, Maxset is the modulus of the maximum solution set, and k is the number of current iterations;.
[0083] Step 304: Update the velocity and position of the particles.
[0084] The speed and position of the particles are updated according to formulas (7) and (8). As it is the prior art, it will not be repeated here.
[0085] Step 305: Check whether any particles in the particle swarm are out of bounds, and if the particles are out of bounds, correct them to the boundary of the solution domain.
[0086] When the particle position is updated, the particle may cross the boundary. The present invention adopts a position correction strategy. The main idea of the strategy is to check whether the element of each dimension of each particle exceeds the limited range. If it exceeds the limited range, it will It is corrected to the boundary value.
[0087] Suppose the i-th dimension particle X of each particle X i , Its limited range is [D min ,D max ], the out-of-bounds adjustment method is shown in formula (11):
[0088] X i = D max , X i D max D min , X i D min - - - ( 11 )
[0089] Among them, D min , D max These are the lower and upper limits of the elements in each particle.
[0090] Step 306: Check whether the algorithm termination condition is met (for example, the preset maximum number of iterations or the preset prediction accuracy is reached), if yes, the algorithm ends and go to step 4; otherwise, return to step 303 and continue iteration;
[0091] Step 4. Decoding the global optimal extremum gbest of the last iteration to obtain the optimized connection weight and threshold of the neural network.
[0092] At this point, the optimized PSO-Elman prediction model is obtained, and the prediction model can be used to predict server performance at a future time. The construction process of PSO-Elman predictive model is as follows image 3 Shown.
[0093] Assuming that there are M servers in a cloud environment, 200 consecutive CPU performance records are selected from one of the servers, and each group of 20 forms a sample, a sample set of 10 samples in total, of which each sample is 10 Time series (x i 1 ,x i 2...x i 10 }, where i represents the i-th sample. x i 10 For the moment that needs to be predicted. The number of input layer nodes of the neural network is m, the number of hidden layer nodes is n, and the number of output layer nodes is r. Set the group size N=20, the maximum number of iterations G=100, the inertia weight w=0.5, the initial velocity of each particle v=0, the learning position is limited to [-1, 1], the learning factor c 1 =c 2 =0.7, the target error is 0.001, and the aggregation threshold η is 0.7. On this basis, the PSO-Elman prediction model of the present invention is constructed, specifically as follows:
[0094] Step 1: Initialize
[0095] 1. Design the Elman network structure according to the training samples, calculate the elements and x in each sample sequence i 10 The correlation coefficient of, forming {ρ 1 i , Ρ 2 i ,...,Ρ 9 i } Correlation coefficient sequence, if ρ 7 i Less than 0, the following ρ 8 i And ρ 9 i Are greater than or equal to 0, then m i = 2. Finally, the number of input layer nodes m is m i The average value of the sequence is assumed to be 3, the number of hidden layer nodes is 6, and the number of nodes in the output layer is 1.
[0096] 2. Determine the size of the particle swarm, the position and velocity of the particle, and the learning factor c 1 =c 2 =0.7 and inertia weight w=0.5, where the dimension of each particle is 3×6+6×6+6×1+1=61.
[0097] 3. Initialize the population, randomly generate N=20 particles, the length is L=61, and the population set is A.
[0098] Step 2: Iterative update
[0099] 1. Calculate the fitness of particles in particle swarm A, and calculate the fitness of all particles according to formula (6).
[0100] 2. Update the current individual extreme value pbest of each particle and the global optimal extreme value gbest of the particle population.
[0101] 3. Calculate the aggregation degree of the particle swarm according to formula (10). If the aggregation degree is greater than the threshold η=0.7, the optimal particles are retained and n-1 displacement increments are randomly generated. The range of the displacement increment is Update the positions of n-1 particles in the particle swarm except for the optimal particle.
[0102] 4. Update the velocity and position of the particles according to formula (7) and formula (8).
[0103] 5. Check whether any particles in the particle swarm are out of bounds. If the particles are out of bounds, use formula (11) to correct them to the boundary of the solution domain.
[0104] 6. Check whether the number of algorithm iterations has reached the maximum number of iterations G=100 or whether it has reached the set prediction accuracy of 0.001. If the termination condition is met, the global optimal solution gbest of the last iteration will be the weight and threshold of the Elman neural network , The algorithm ends, otherwise it returns 3 and the algorithm continues to iterate.
[0105] Step 3: Result output
[0106] According to the number of neurons in each layer of the input layer, hidden layer, structure layer and output layer, the optimal solution gbest is converted into the weights and thresholds of each layer of the Elman network, and the weights and thresholds are used to construct the Elman neural network. As predicted, the algorithm ends.
[0107] The prediction model proposed by the present invention maintains good accuracy in both short-term prediction and long-term prediction, and improves the training speed of the neural network.
