Efficient spatial nearest neighbor query method for highway networks
A query method and nearest-neighbor technology, applied in special data processing applications, instruments, electrical digital data processing, etc., can solve problems such as large query time and increased overhead
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
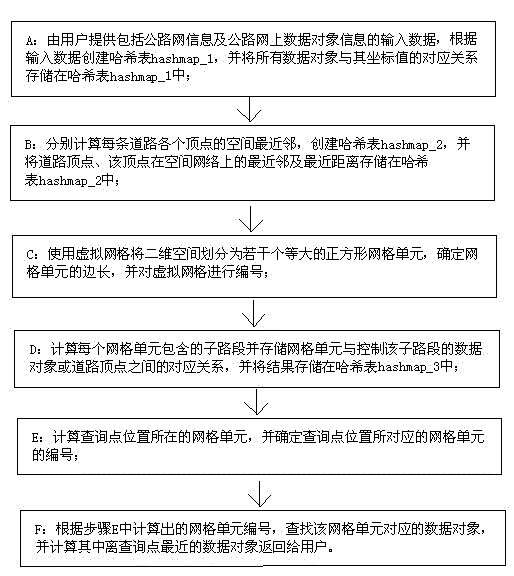
[0042] like figure 1 As shown, the highway network efficient spatial nearest neighbor query method of the present invention comprises the following steps, wherein A, B, C, and D steps are used in the offline index building stage; E, F steps are used in the real-time spatial query processing stage:
[0043] A: The user provides input data including road network information and data object information on the road network, creates a hash table hashmap_1 based on the input data, and stores the correspondence between all data objects and their coordinate values in the hash table hashmap_1; the hash table The primary key of hashmap_1 is the unique identifier oid of the data object, and the value is the coordinate value of the data object.
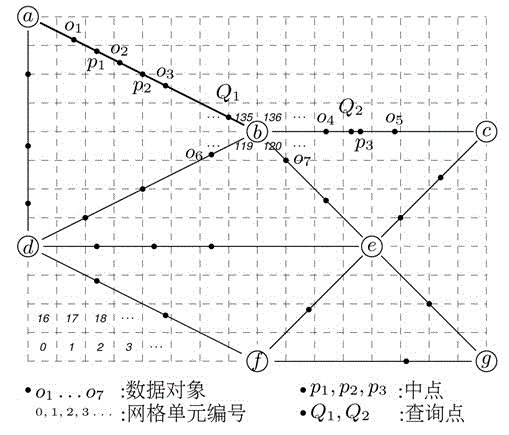
[0044] B: Calculate the spatial nearest neighbors of each vertex of each road, create a hash table hashmap_2, and store the road vertex, the nearest neighbor and the nearest distance of the vertex on the spatial network in the hash table hashma...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com