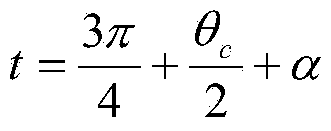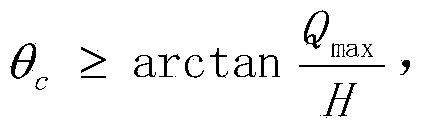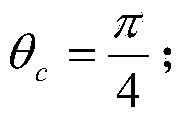Modeling method for compound parabolic concentrator for linear Fresnel light condensing and heat collecting system on basis of matlab

A linear Fresnel and compound paraboloid technology, applied in the modeling field of compound parabolic concentrators, can solve problems such as inability to realize optimal design, impossibility of optical simulation, long design cycle, etc., and achieve rapid quantitative analysis and easy optimization The effect of design, accurate calculation

Active Publication Date: 2014-05-21
兰州大成科技股份有限公司 +2
View PDF2 Cites 18 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0003] The solar vacuum heat collection tube used in the linear Fresnel concentrating heat collection system is covered with a glass outer tube outside the metal inner tube coated with a high-temperature resistant selective absorption film, and due to installation requirements, the glass outer tube of the h

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Modeling method for compound parabolic concentrator for linear Fresnel light condensing and heat collecting system on basis of matlab
  • Modeling method for compound parabolic concentrator for linear Fresnel light condensing and heat collecting system on basis of matlab
  • Modeling method for compound parabolic concentrator for linear Fresnel light condensing and heat collecting system on basis of matlab

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0034] Example 1: see figure 2 , a method for modeling a compound parabolic concentrator based on a matlab-based linear Fresnel concentrator system, is characterized in that it includes the following steps:

[0035] 1) The maximum receiving half angle of CPC is obtained from the height of CPC from the ground and the maximum width of Fresnel reflector field

[0036] 2) Taking the outer diameter R=45mm of the metal inner tube of the vacuum heat collecting tube as the base circle of the involute, and establishing a rectangular coordinate system with its center as the origin, the parametric coordinate equation of the involute in the left half of the CPC is:

[0037] x=-45(sint-tcost) (1);

[0038] y=45(cost+tsint) (2);

[0039] 3) Rotate the involute α=50.4489° around the center O, so that t=t on the involute 0 The point C is on the CPC central axis, t 0 Satisfy the following equation:

[0040] x ( ...

Embodiment 2

[0060] Example 2: see figure 2 , a method for modeling a compound parabolic concentrator based on a matlab-based linear Fresnel concentrator system, is characterized in that it includes the following steps:

[0061] 1) The maximum receiving half angle of CPC is obtained from the height of CPC from the ground and the maximum width of Fresnel reflector field

[0062] 2) Taking the outer diameter R=45mm of the metal inner tube of the vacuum heat collecting tube as the base circle of the involute, and establishing a rectangular coordinate system with its center as the origin, the parametric coordinate equation of the involute in the left half of the CPC is:

[0063] x=-45(sint-tcost) (1);

[0064] y=45(cost+tsint) (2);

[0065] 3) Rotate the involute α=50.4489° around the center O, so that t=t on the involute 0 The point C is on the CPC central axis, t 0 Satisfy the following equation:

[0066] x ( ...

Embodiment 3

[0080] Embodiment 3: see figure 2 , a method for modeling a compound parabolic concentrator based on a matlab-based linear Fresnel concentrator system, is characterized in that it includes the following steps:

[0081] 1) The maximum receiving half angle of CPC is obtained from the height of CPC from the ground and the maximum width of Fresnel reflector field

[0082] 2) Taking the outer diameter R=45mm of the metal inner tube of the vacuum heat collecting tube as the base circle of the involute, and establishing a rectangular coordinate system with its center as the origin, the parametric coordinate equation of the involute in the left half of the CPC is:

[0083] x=-45(sint-tcost) (1);

[0084] y=45(cost+tsint) (2);

[0085] 3) Rotate the involute α=50.4489° around the center O, so that t=t on the involute 0 The point C is on the CPC central axis, t 0 Satisfy the following equation:

[0086] x ( ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

PUM

PropertyMeasurementUnit
Outer diameteraaaaaaaaaa
Login to view more

Abstract

The invention relates to a modeling method for a compound parabolic concentrator (CPC) for a linear Fresnel light condensing and heat collecting system on the basis of matlab. The modeling method comprises the following steps: 1, determining the maximum receiving half angle theta c of the CPC; 2, using an outer diameter circle of a metal inner pipe of a vacuum heat collecting tube as a base circle of an involute; 3, rotating the involute by an angle alpha by using a circle center O as the center, so that a point C on the involute, which meets the condition that t=t0, is positioned on a center shaft of the CPC and the distance between the point C and the metal inner tube of the heat collecting tube is the sum of the distance between the point and a glass outer tube of the heat collecting tube and the distance between the glass outer tube and the metal inner tube of the heat collecting tube; 4, using a point on the involute, which meets the condition (refer to the specification), as a junction point of an involute CFB and a parabola A; 5, rotating the parabola by an angle theta c around the vertex of the parabola to enable the parabola to pass through a left junction point FB and using a right junction point FA as a focus to obtain a parabolic equation; 6, carrying out simulating calculation on a relation of a convergence rate and an intercepting ratio of the CPC by utilizing a ray tracing method, and selecting the suitable intercepting ratio.

Description

technical field [0001] The invention relates to a modeling method of a compound parabolic concentrator, in particular to a modeling method of a CPC (Compound Parabolic Concentrator: CPC) for a linear Fresnel type concentrating heat collection system based on matlab software. Background technique [0002] The structure of an ideal single-tube compound parabolic concentrator (Compound Parabolic Concentrator: CPC) is as follows figure 1 shown. A and B are two parabolas symmetrical about the central axis of CPC, F A and F B are the foci of A and B respectively, aF A and bF B Parallel to the principal axes of parabolas B and A respectively, the included angle is the maximum acceptance angle 2θ of CPC c . f B C. CF A It is two sections of involutes with the outer circle of the heat-absorbing tube as the base circle, which are also symmetrical about the central axis of the CPC. From the nature of the involute of the circle, it can be seen that the light from any direction ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

Application Information

Patent Timeline
no application Login to view more
IPC IPC(8): G06F17/50
Inventor 范多旺王成龙马军范多进王云锋
Owner 兰州大成科技股份有限公司
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Try Eureka
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap