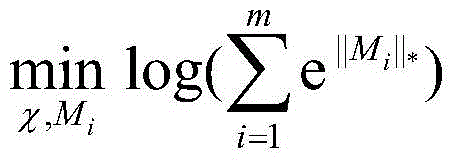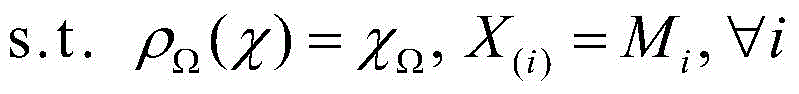A Tensor Recovery Method Based on Exponentialized Kernel Norm and Mixed Singular Value Truncation
A recovery method and nuclear norm technology, applied in image data processing, instrumentation, computing, etc., can solve problems such as difficulty in obtaining local optimum, difficulty in directly optimizing CP rank, difficulty in selecting weights, etc., to achieve tensor recovery, fast Efficient Tensor Recovery, Effect of Reduced Complexity
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
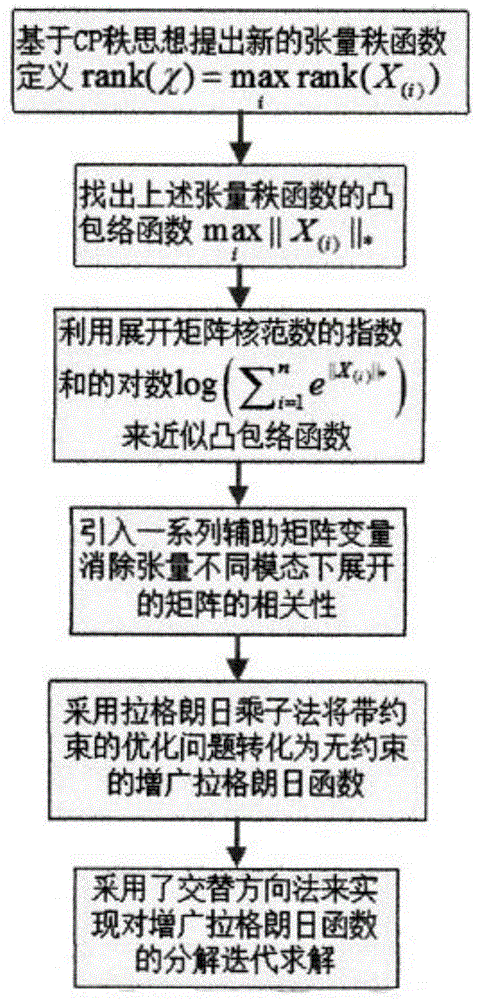
[0025] see figure 1 ,本发明提供一种基于指数化核范数与混合奇异值截断的张量恢复方法,包括以下三个步骤:
[0026] (1)提出一种新的张量秩定义:张量不同模态下展开矩阵秩的最大值;该定义是张量CP秩的下界,能够有效的逼近CP秩,并消除了权重参数的影响,采用核范数指数和的对数来逼近该张量秩定义,将其转化为凸函数;
[0027] (2)为了消除张量不同模态下展开的矩阵的相关性,引入一系列辅助变量来代替展开矩阵,并将约束条件利用拉格朗日乘子法转化为增广拉格朗日函数;
[0028] (3)采用交替方向法对增广拉格朗日函数中各类变量进行迭代优化,直到收敛;其中,对于核范数的指数和中的优化变量,采用混合奇异值截断算法来获得解析解。
[0029] 作为优选的,本实施例所述的步骤(1)具体包括以下子步骤:
[0030] 首先,根据张量CP秩和Tucker秩的优缺点,提出一种新的张量秩定义:张量展开矩阵秩的最大值;
[0031] 其次,将展开矩阵的秩松弛为展开矩阵的核范数,并且利用核范数的指数和的对数来逼近最大值函数,从而将上述张量的秩定义转化为凸函数。
[0032] 作为优选的,本实施例所述的步骤(2)具体包括以下子步骤:
[0033] 首先,由于张量在不同模态下的展开矩阵具有相关性,引入一系列辅助矩阵变量来替换不同模态下的展开矩阵,并增加对应的约束条件;
[0034] 其次,采用拉格朗日乘子法将所有约束条件加入到目标函数中,获得增广拉格朗日函数。
[0035] 作为优选的,本实施例所述的步骤(3)具体包括以下子步骤:
[0036] 首先,为了对增广拉格朗日函数中的不同变量进行分别优化,采用交替方向法对增广拉格朗日函数中的各类变量进行迭代优化;
[0037] 其次,对于核范数指数中的优化变量,采用混合奇异值截断算法来获得解析解。
[0038] 本发明的方法具体运行的硬件和编程语言并不限制,用任何语言编写都可以完成,为此其它工作模式不再赘述。
[0039] 本发明的实施例采用一台具有Intel Core-i3中央处理器和4G字节内存的计算机并用Matlab语言编制了基于指数化核范数与混合奇异值截断的张量恢复的工作程序,实现了本发明的方法。
[0040] 本发明的...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com