Evaluation method of sphericity error based on error sphere
An error evaluation and error sphere technology, which is applied in the field of spherical error evaluation based on error spheres, can solve the problems of not meeting the minimum area conditions, not being accurate enough, and premature, etc., to speed up the evaluation speed, avoid calculations, and improve efficiency.
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment 1
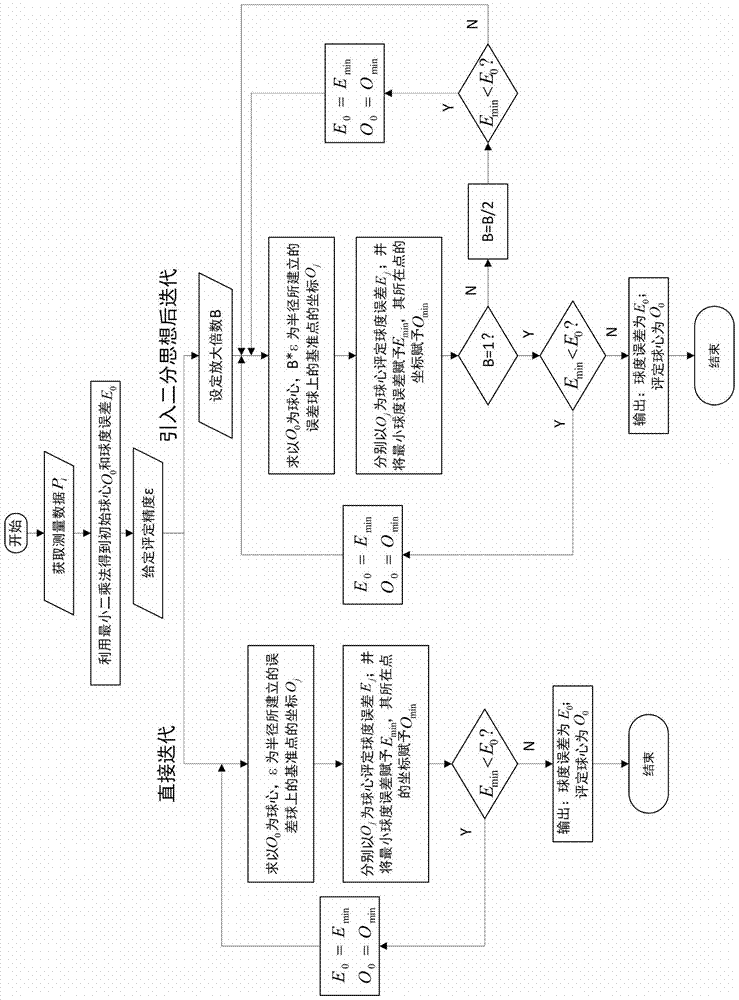
[0047] exist image 3 In the iterative flow chart of an error sphere-based sphericity error evaluation method shown, direct iteration includes the following steps:
[0048] Step 1: Obtain the coordinates and initial data of the measurement point. Measure and obtain the coordinates P of the spherical point i (x i ,y i ,z i ), i=1,2,...,n; n is the number of measuring points. The approximate linear model of the least square method is used to obtain the initial evaluation parameters, and the least square sphere center is used as the initial sphere center, and the evaluated sphericity error is used as the initial sphericity error.
[0049] The objective function of its linear model is:
[0050]
[0051] where x 0 ,y 0 ,z 0 is the center of the least squares sphere, r is the radius of the least squares; D=-2Ax 0 ,E=-2Ay 0 ,F=-2Az 0 ,
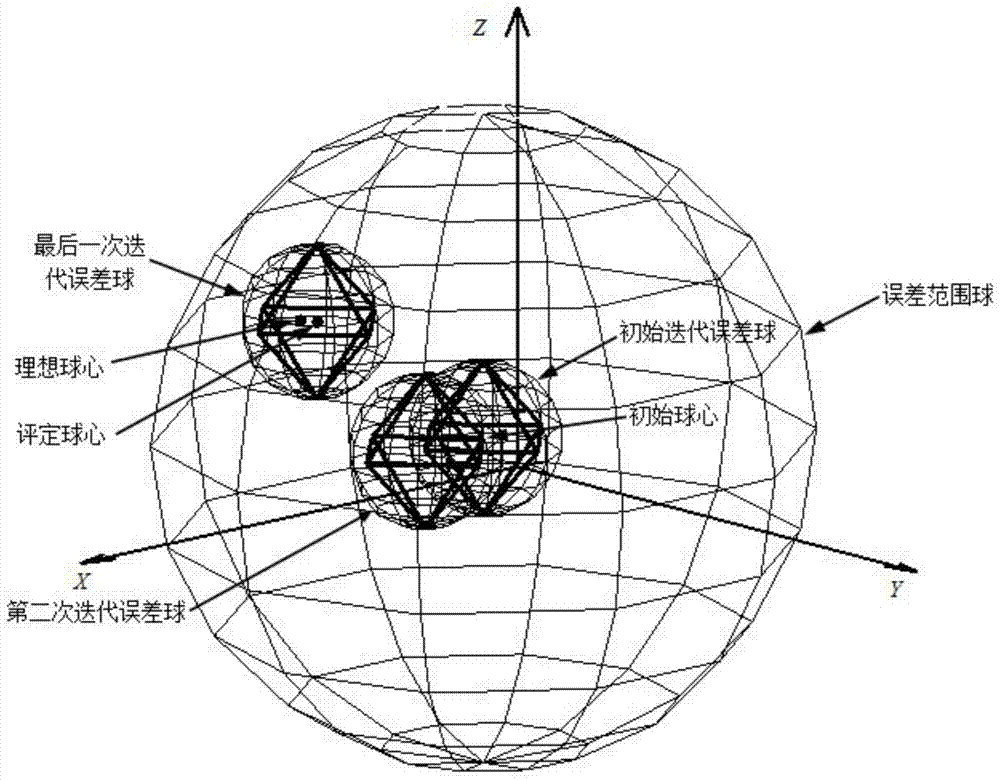
[0052] then the initial center Initial sphericity error E 0 =ΔR=maxR 0 -minR 0 ,in i=1,2,...,n.
[0053] Step 2: Determi...
Embodiment 2
[0064] Introduce the idea of dichotomy for iteration, including the following steps:
[0065] Step 1: Obtain the coordinates and initial data of the measurement point. Measure and obtain the coordinates P of the spherical point i (x i ,y i ,z i ), i=1,2,...,n; n is the number of measuring points. The approximate linear model of the least square method is used to obtain the initial evaluation parameters, and the least square sphere center is used as the initial sphere center, and the evaluated sphericity error is used as the initial sphericity error.
[0066] The objective function of its linear model is:
[0067]
[0068] where x 0 ,y 0 ,z 0 is the center of the least squares sphere, r is the radius of the least squares; D=-2Ax 0 ,E=-2Ay 0 ,F=-2Az 0 ,
[0069] then the initial center Initial sphericity error E 0 =ΔR=maxR 0 -minR 0 ,in i=1,2,...,n.
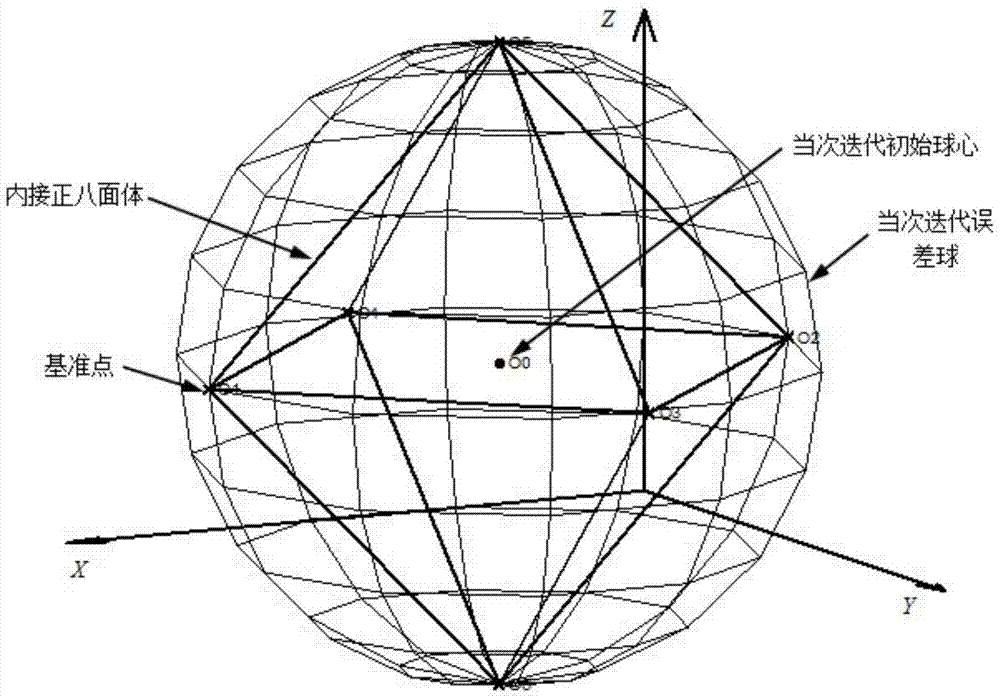
[0070] Step 2: Determine the optimization space. With the initial center O obtained in step 1 0 is...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com