Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Disturbance Estimation Method for Gyro Flywheel System Based on Extended High Gain Observer

A technology of high-gain observer and gyro flywheel, applied in the field of inertial navigation

Inactive Publication Date: 2017-11-14
HARBIN INST OF TECH
View PDF3 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0005] In order to solve the dynamic disturbance estimation problem of the gyro flywheel in the working state of a large tilt angle, the present invention proposes a method for estimating the disturbance of the gyro flywheel system based on an extended high-gain observer, comprising the following steps:

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Disturbance Estimation Method for Gyro Flywheel System Based on Extended High Gain Observer
  • Disturbance Estimation Method for Gyro Flywheel System Based on Extended High Gain Observer
  • Disturbance Estimation Method for Gyro Flywheel System Based on Extended High Gain Observer

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

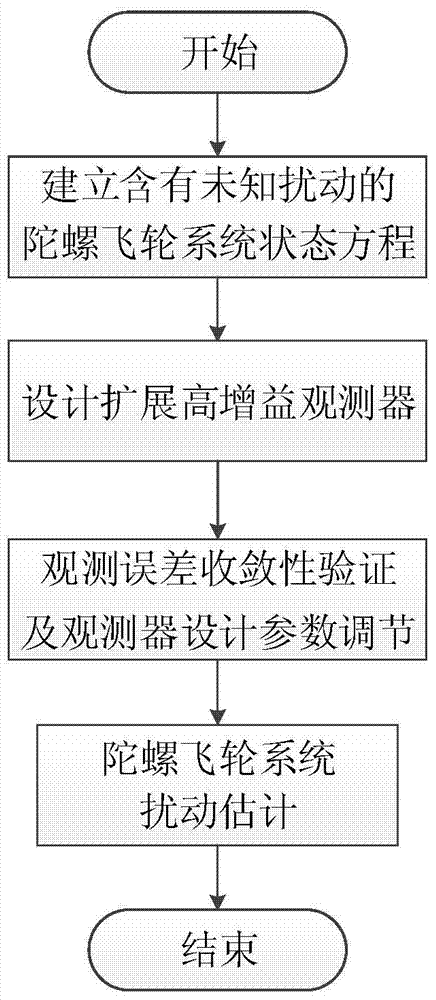
[0083] Specific implementation manner 1: The disturbance estimation method of the gyro flywheel system based on the extended high-gain observer of this embodiment is implemented according to the following steps:

[0084] Step 1: According to the dynamic equation of the gyro flywheel system, establish the state equation of the gyro flywheel system with unknown disturbance;

[0085] Step 2: According to the state equation of the gyro flywheel system with unknown disturbances, design an extended high gain observer;

[0086] Step 3: Observation error convergence and observer design parameter ε adjustment;

[0087] Step four, realize the disturbance estimation of the gyro flywheel system.

specific Embodiment approach 2

[0088] Embodiment 2: The difference between this embodiment and Embodiment 1 is that it is characterized in that the state equation of the gyro flywheel system with unknown disturbance in step 1 is implemented in the following steps:

[0089] The tilt angle of the rotor of the gyro flywheel in two dimensions (φ x ,φ y ) And inclination angular velocity As the state variable x: Then the state equation of the gyro flywheel system with unmodeled disturbance is shown in formula (1):

[0090]

[0091] The measurement equation is shown in formula (2):

[0092]

[0093] Where f 1 (x,t),f 2 (x,t) represents the nonlinear mechanism term of the gyro flywheel under ideal conditions; u x ,u y Represents the control torque of the two-dimensional torque device, g x1 (x,t),g x2 (x,t),g y1 (x,t),g y2 (x, t) represents the nonlinear coefficient term of the two-dimensional torque device;

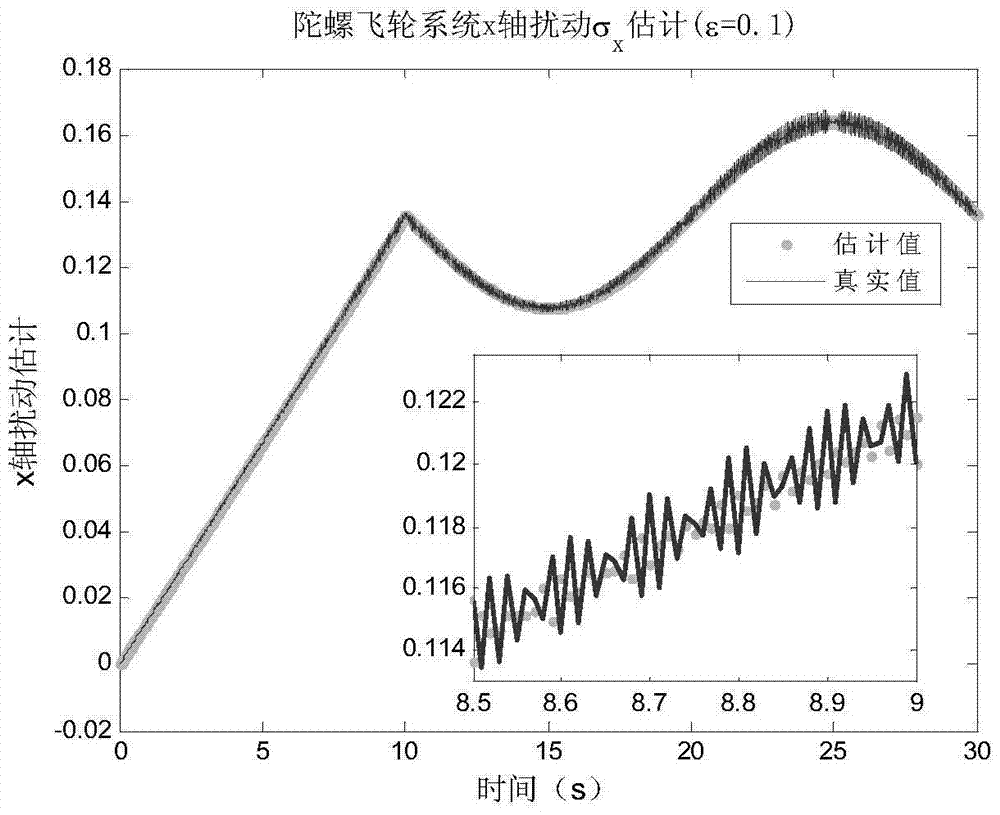
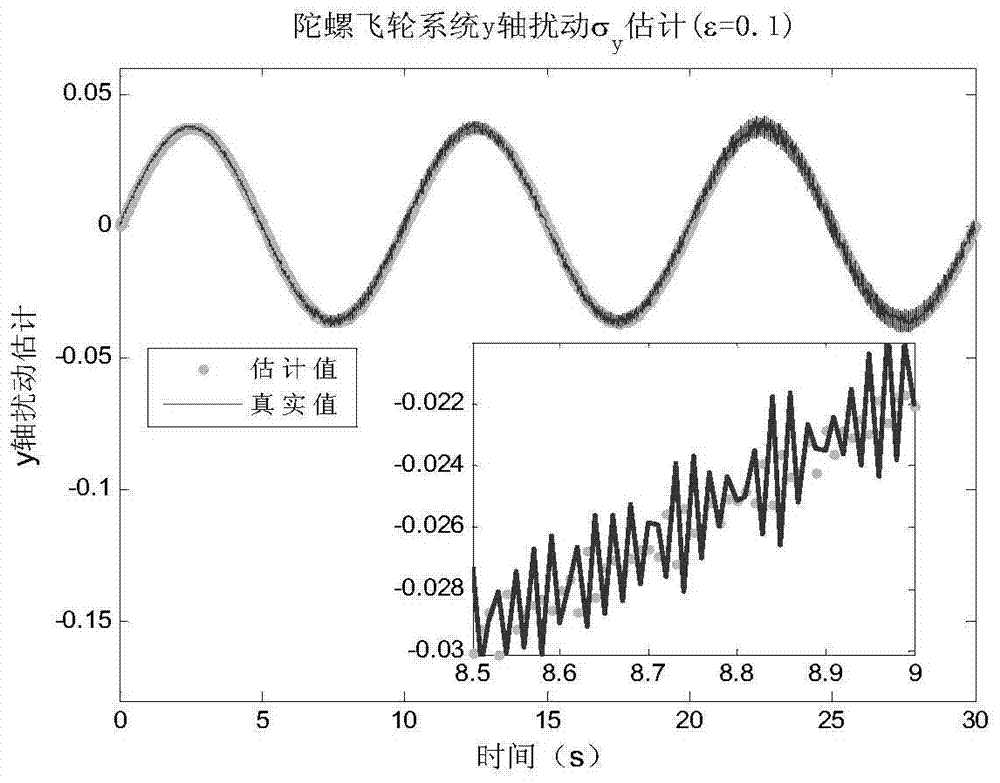
[0094] σ x (x,t),σ y (x,t) represents the unmodeled disturbance term of the system; y 1 ,y 2 Respectively represe...

specific Embodiment approach 3

[0116] Specific implementation manner 3: This implementation manner is different from specific implementation manners one or two in that it is characterized in that the design of the extended high gain observer in the second step is implemented in the following steps:

[0117] The measurement equation y=Cx is used to realize the control of the state variable x and the nonlinear disturbance term σ d The estimation of (x,t) is designed as follows to extend the high gain observer:

[0118]

[0119] among them, Is the state variable of the high gain observer; To expand the state variable of the high gain observer;

[0120] H(ε), F(ε) are the gain matrix of the observer, and its specific form is as follows:

[0121]

[0122] Among them, the design parameter ε> 0 is a small design parameter; design parameter α ij ,i=1,2,3,j=1, 2 are all selected as real numbers, and should satisfy the following Hurwitz polynomial:

[0123] s 3 +α 1j s 2 +α 2j s+α 3j ,j=1,2

[0124] Other steps and parameter...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides an extended high-gain observer based disturbance estimation method for a gyrowheel system, belongs to the field of inertial navigation and aims to solve the problem about dynamic disturbance estimation of a gyrowheel rotor in a large heeling angle working state. The method comprises the following steps: step 1, a gyrowheel system state equation containing unknown disturbance is established according to a kinetic equation of the gyrowheel system; step 2, an extended high-gain observer is designed according to the gyrowheel system state equation containing unknown disturbance; step 3, observation error convergence is verified and an observer design parameter epsilon is adjusted; step 4, disturbance estimation of the gyrowheel system is performed. The extended high-gain observer based disturbance estimation method is applicable to disturbance estimation of the gyrowheel system.

Description

Technical field [0001] The invention is a gyro flywheel system disturbance estimation method based on an extended high gain observer, and specifically relates to the field of inertial navigation. Background technique [0002] Gyro flywheel is an electromechanical servo device with both actuator and sensor functions used in spacecraft. It is developed based on the physical structure of a traditional inertial instrument—dynamic tuning gyroscope. However, the obvious difference between the gyro flywheel and the dynamic tuning gyroscope is that the gyro flywheel not only realizes the same two-dimensional carrier angular rate measurement function as the dynamic tuning gyroscope, but also realizes the three-dimensional control torque output function. In order to realize the three-dimensional torque output function of the gyro flywheel, the gyro flywheel rotor needs to produce a large angle of tilting movement in the two-dimensional radial direction, and the speed adjustment movement in...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G01C25/00
CPCG01C25/005
Inventor 刘晓坤赵辉马克茂霍鑫史维佳姚郁
Owner HARBIN INST OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com