Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

An implicit staggered grid finite-difference elastic wave numerical simulation method and device

A staggered grid and finite difference technology, applied in the field of seismic wave exploration, can solve problems such as poor accuracy, achieve the effects of improving numerical solution accuracy, improving calculation efficiency, and reducing calculation time

Active Publication Date: 2017-05-03
INST OF GEOLOGY & GEOPHYSICS CHINESE ACAD OF SCI
View PDF1 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0043] The present invention provides an implicit staggered grid finite-difference elastic wave numerical simulation method and device to at least solve the problem of poor accuracy of seismic wave numerical simulation methods in the related art

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • An implicit staggered grid finite-difference elastic wave numerical simulation method and device
  • An implicit staggered grid finite-difference elastic wave numerical simulation method and device
  • An implicit staggered grid finite-difference elastic wave numerical simulation method and device

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

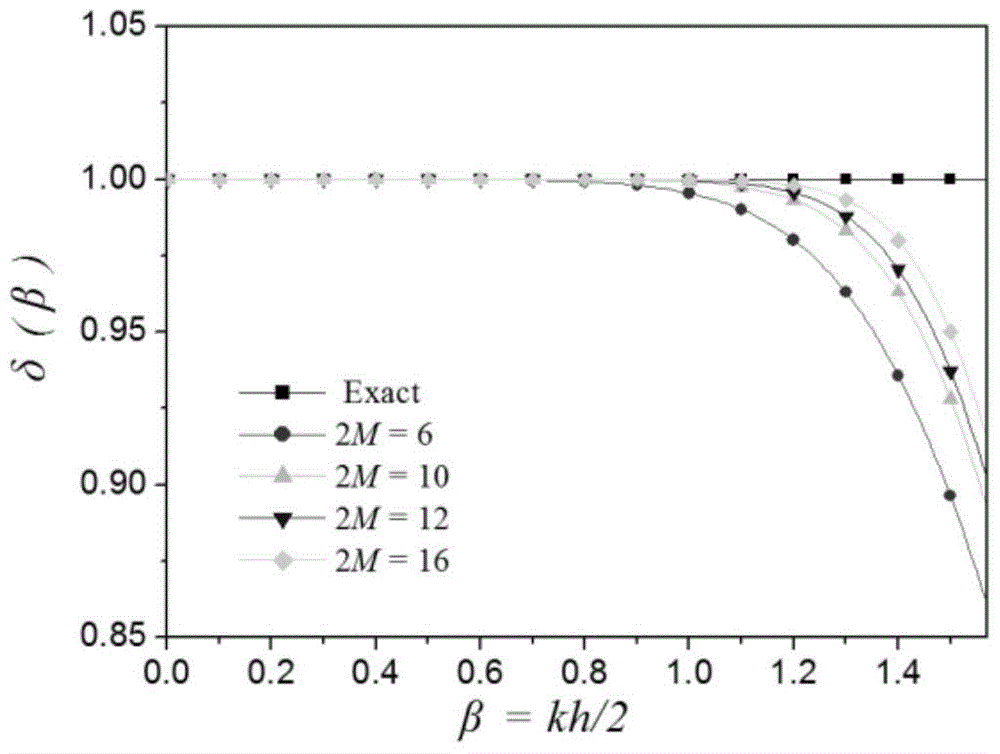
[0075] This embodiment provides an implicit staggered grid finite difference elastic wave numerical simulation method, Figure 4 is a flow chart of an implicit staggered grid finite difference elastic wave numerical simulation method according to an embodiment of the present invention, as shown in Figure 4 As shown, the method includes the following steps (step S401-step S405):

[0076] Step S401, based on the implicit staggered grid finite difference scheme (ie the above formula 2) and the plane wave theoretical formula (ie the above formula 5), ​​the dispersion relation expression (ie the above formula 8) is obtained:

[0077] where, β=kh / 2, k is the wave number, h is the grid size, b is a constant, M is the order, a m are implicit staggered grid finite difference coefficients, m=1,2,...,M.

[0078] Step S402, performing a sampling approximation method on the dispersion relation expression to obtain a linear algebraic equation system.

[0079] Specifically: uniformly t...

Embodiment approach

[0087] In the first step, the implicit staggered grid finite difference coefficient a m and the constant b are substituted into the implicit staggered grid finite difference scheme to solve the spatial partial derivatives in the elastic wave equation;

[0088] This step specifically includes: the implicit staggered grid finite difference coefficient a m and the constant b are substituted into the implicit staggered grid finite difference scheme, and the implicit staggered grid finite difference scheme is applied to each grid point, and the difference equations on all grid points are simultaneously established (the implicit staggered grid finite difference equation is obtained through the above-mentioned implicit staggered grid finite-difference format conversion), and the tridiagonal matrix equation is obtained; the spatial partial derivatives in the elastic wave equation are obtained by solving the tridiagonal matrix equation.

[0089] In the second step, the spatial partial...

Embodiment 2

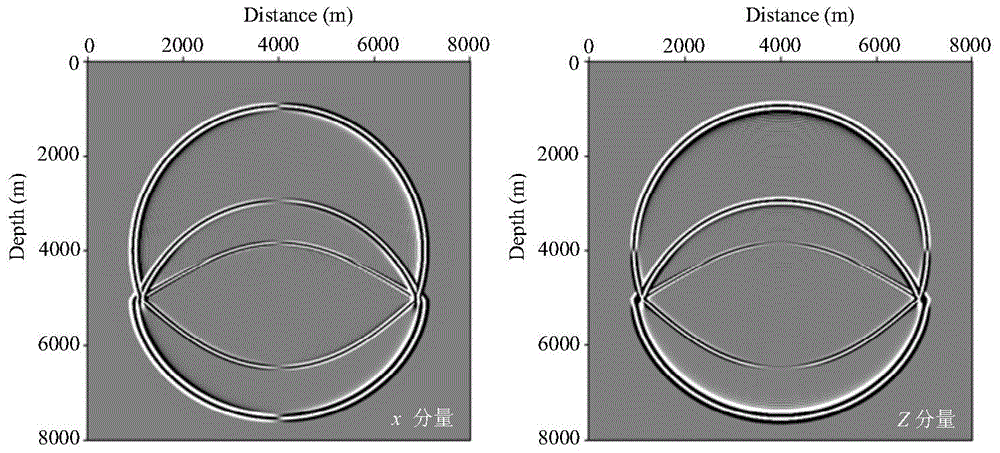
[0094] This embodiment introduces the complete flow of the implicit staggered grid finite-difference elastic wave numerical simulation method.

[0095] In a homogeneous isotropic medium, the two-dimensional elastic wave equation (Equation 1) is expressed as:

[0096]

[0097] Among them, t represents time, x and z represent space coordinates, (v x ,v z ) is the velocity vector, (τ xx ,τ zz ,τ xz ) is the stress tensor, ρ is the density, and λ and μ are the Lame constants. The time derivative term in the elastic wave equation (formula 1) (that is, the items on the left side of the equal sign in formula 1) is solved by the second-order difference scheme, and in order to improve the solution accuracy, the spatial derivative term (that is, the items on the right side of the equal sign in formula (1)) Solved by the implicit staggered-grid finite-difference scheme (Equation 2) described below.

[0098] The spatial first derivative of the function p(x) is expanded into an im...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses an implicit staggered-grid finite difference elastic wave numerical simulation method and device. The method comprises the steps that a dispersion relation expression is obtained based on an implicit staggered-grid finite difference scheme and a plane wave theoretical formula; (M+1) discrete points are evenly taken within the value range of beta in the dispersion relation expression, and the left and right sides of the dispersion relation expression are set to be equal on the discrete points so that a linear algebraic equation set is obtained; the linear algebraic equation set is solved so that the implicit staggered-grid finite difference coefficient am and constant b are obtained; an elastic wave equation is solved based on the implicit staggered-grid finite difference coefficient am, the constant b and the implicit staggered-grid finite difference format; and a wave field diagram is generated according to the solving result and wave field analysis is performed according to the wave field diagram. The solving error of the elastic wave equation can be reduced and the numerical solution accuracy can be enhanced so that a more accurate wave field stimulation record can be obtained. When the same calculation error is constrained, calculation time can be reduced and calculation efficiency can be enhanced.

Description

technical field [0001] The invention relates to the technical field of seismic wave exploration, in particular to an implicit staggered grid finite difference elastic wave numerical simulation method and device. Background technique [0002] The numerical simulation of seismic wave field is the link between reflection seismology, which takes reflection waves as the main research topic, and drilling, logging, geology and reservoir engineering, which takes rock strata as the main research topic. The application of its technology almost runs through seismic data. Acquisition, processing, interpretation and all aspects of oil and gas reservoir development engineering. The numerical simulation method is to simplify the specific geological and geophysical problems appropriately to form a mathematical model, solve the mathematical and physical equations of the model by numerical methods, and then simulate and study the propagation of seismic waves based on this. Seismic wave numer...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G01V1/28
Inventor 杨蕾严红勇刘洪
Owner INST OF GEOLOGY & GEOPHYSICS CHINESE ACAD OF SCI
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com