Fuzzy clustering method based on sparse mean values
A fuzzy clustering method and mean value technology, applied in the computing field, can solve problems such as poor processing results and inability to effectively measure the similarity between sample points and classes
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
[0026] The present invention will be described in further detail below in conjunction with the examples, but the protection scope of the present invention is not limited thereto.
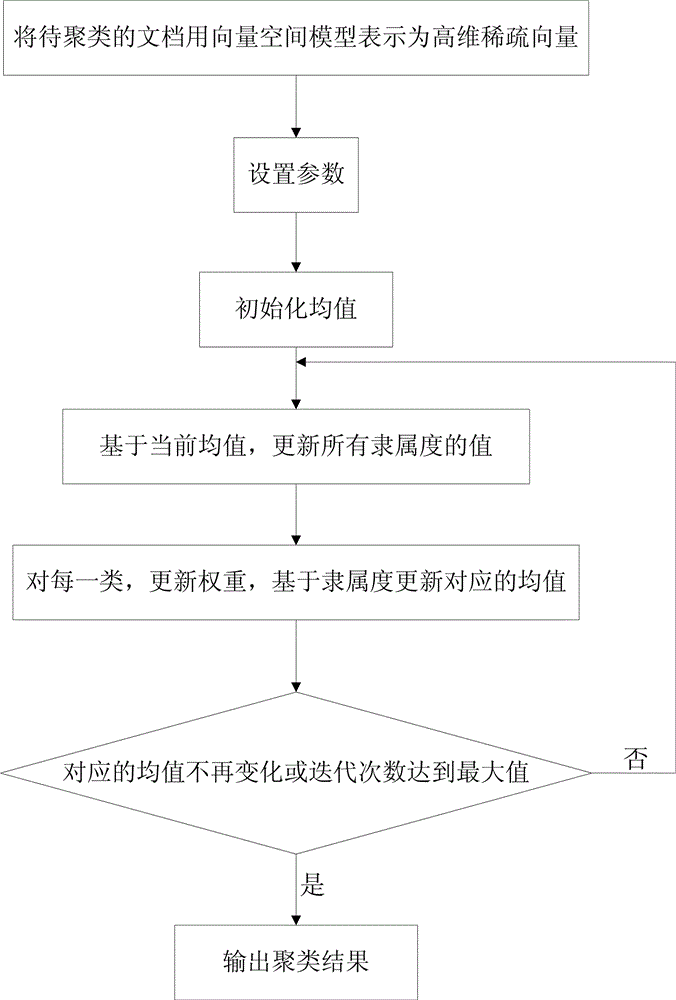
[0027] As shown in the figure, the present invention relates to a fuzzy clustering method based on a sparse mean, and the method includes the following steps:
[0028] Step 1.1: Express the documents to be clustered as a high-dimensional sparse vector X={x 1 ,x 2 ,...x n}, where each sample point is s dimension vector, i.e. x i ∈ R s , s>0, 1≤i≤n; n is the total number of samples, n>0;
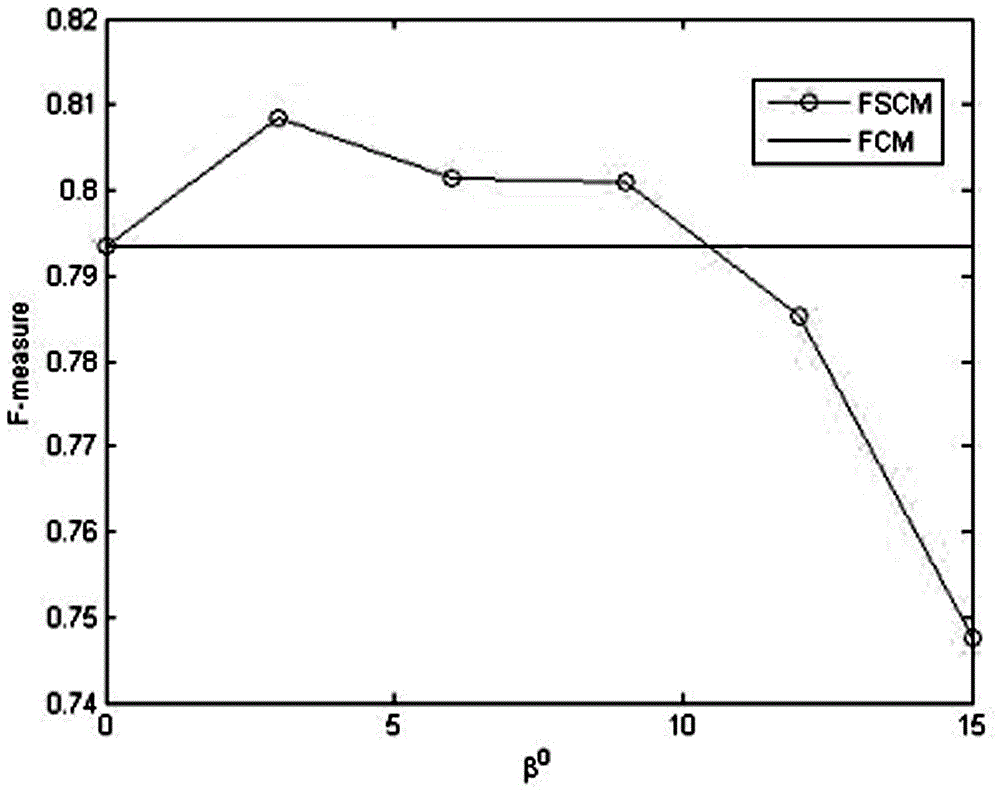
[0029] Step 1.2: Set the parameters, which include the number of classes k, the fuzzy coefficient m, and the weight of the initial regularization term β 0 , the end judgment parameter ε and the maximum number of iterations T; 00 >0; set with mean l 1 The objective function for minimizing the norm regularizer: Among them, u ci Indicates the degree of membership of the i-th sample to the c-th class, δ c Ind...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com