Nonnegative matrix factorization method based on discriminative orthogonal subspace constraint
A non-negative matrix decomposition and orthogonal subspace technology, applied in the field of information processing, can solve the problem of insufficient generalization ability of the algorithm in the test data set, so as to improve generalization performance, good projection dimensionality reduction ability, and generalization ability Improved effect
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment 1
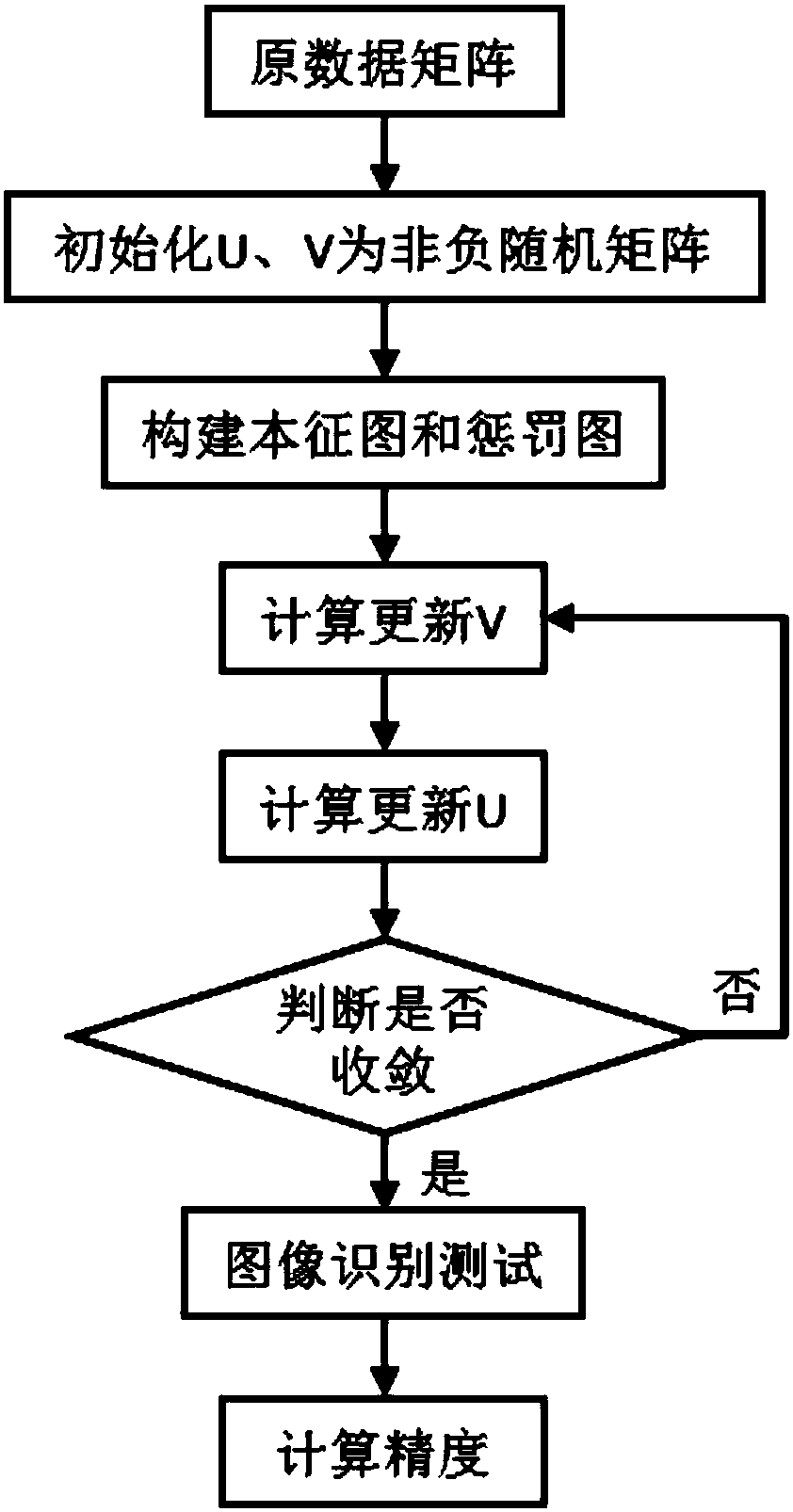
[0044] Embodiment one (with reference to figure 1 )
[0045] Step 1. Decompose the original data matrix under the framework of non-negative matrix factorization based on discriminant orthogonal subspace constraints.
[0046] (1a) Pull each image in the image sample set into a vector to form an m×n original data matrix X, m is the dimension of each sample, and n is the number of samples; in this way, the corresponding training data are obtained Matrix X train and the test data matrix X test ;
[0047] Among them, for the training data matrix X train :
[0048] (1b) Initialize the base matrix U of m×l 0 , l×n encoding matrix V 0 is a non-negative random matrix, l is the subspace dimension to be learned, and the number of iterations t=0;
[0049] (1c) Use the K nearest neighbor algorithm to construct the intrinsic map and the penalty map, and the number of neighbors is set to k 1 and k 2 , to calculate the eigengraph Laplacian matrix L in and the penalized graph Laplac...
Embodiment 2
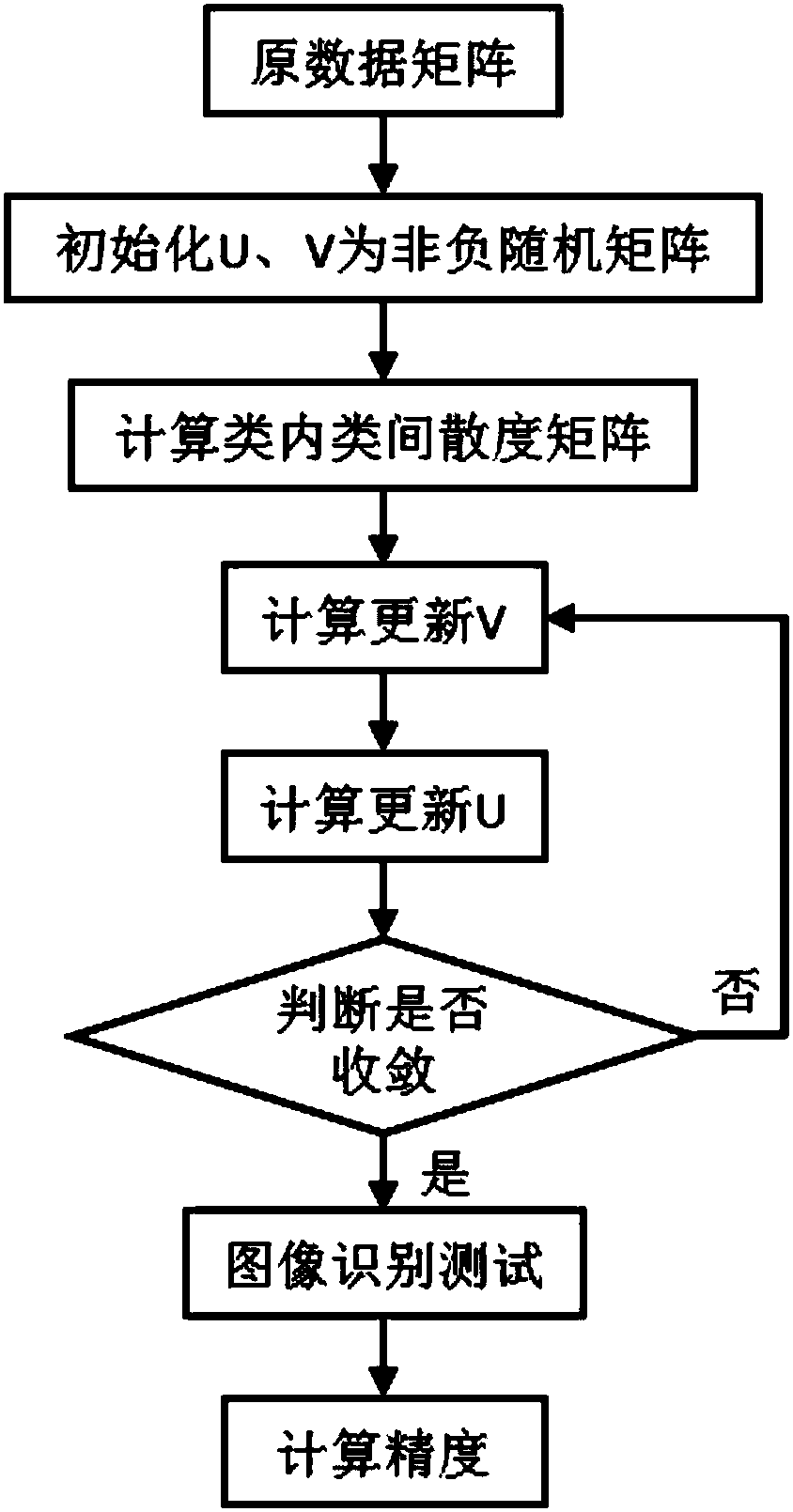
[0069] Embodiment two (with reference to figure 2 )
[0070] Step 1. Decompose the original data matrix under the framework of non-negative matrix factorization based on discriminant orthogonal subspace constraints.
[0071] (1a) Pull each image in the image sample set into a vector to form an m×n original data matrix X, m is the dimension of each sample, and n is the number of samples; in this way, the corresponding training data are obtained Matrix X train and the test data matrix X test ;
[0072] Among them, for the training data matrix X train :
[0073] (1b) Initialize the base matrix U of m×l 0 , l×n encoding matrix V 0 is a non-negative random matrix, l is the subspace dimension to be learned, and the number of iterations t=0;
[0074] (1c) Calculate the intra-class scatter matrix S about the original sample w and between-class scatter matrix S b ;
[0075] (1d) Construct a discriminant regular term based on Fisher's criterion:
[0076] tr(U T S w U)-tr(...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com