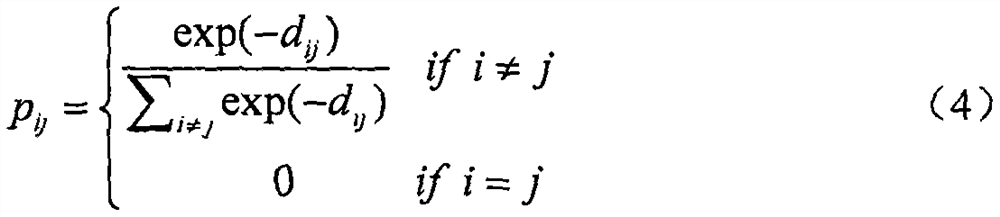A Soft Sensor Method Based on Optimal Selection and Optimal Regression of Orthogonal Components
An optimal selection, soft measurement technology, applied in genetic models, design optimization/simulation, special data processing applications, etc., can solve the problems of staying at the level of improvement of a single algorithm, finding input and output, etc., to achieve soft measurement performance guarantee , to ensure the effect of precision
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
[0049] The method of the present invention will be described in detail below in conjunction with the accompanying drawings.
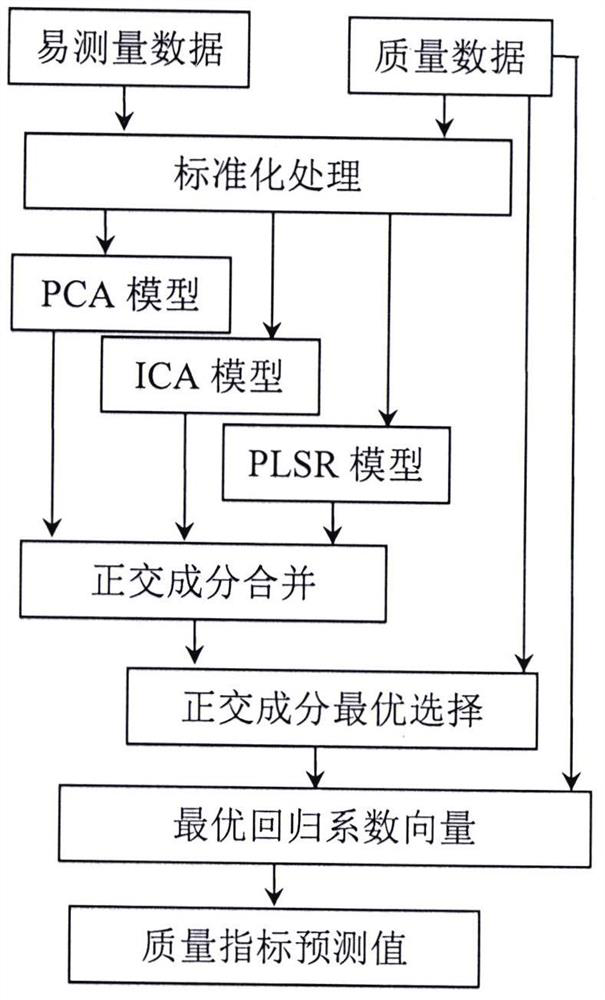
[0050] Such as figure 1 As shown, the present invention discloses a soft sensor method based on optimal selection and optimal regression of orthogonal components. The specific implementation process of the method of the present invention and its superiority over existing methods will be described below in conjunction with an example of a specific industrial process.
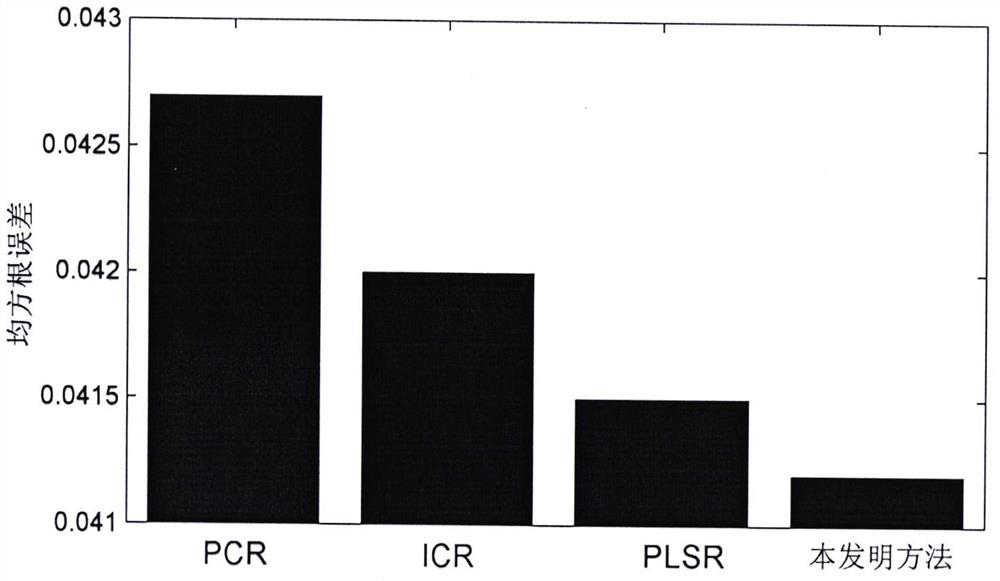
[0051] The application object is from Tennessee-Eastman (TE) chemical process experiment, and the prototype is an actual process flow of Eastman chemical production workshop. At present, the TE process has been widely used as a standard experimental platform for process monitoring and soft sensor research due to its complexity. The whole TE process includes 22 measured variables, 12 manipulated variables, and 19 component measured variables. In this implementation case, 33 easily measur...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com