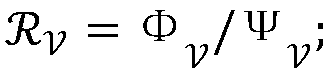Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Numerical calculating method for accelerated solution of burn-up equation by Krylov subspace

A numerical calculation and subspace technology, applied in the field of nuclear engineering, can solve the problems of insufficient precision and high rigidity of the burnup matrix, and achieve the effect of reducing the amount of calculation and improving the calculation efficiency.

Active Publication Date: 2018-10-16
SOUTH CHINA UNIV OF TECH
View PDF8 Cites 2 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

In the calculation of fuel consumption, the rigidity of the fuel consumption matrix is ​​relatively large, and it is a matrix close to singularity. The general Krylov subspace method cannot meet the requirements in terms of accuracy.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Numerical calculating method for accelerated solution of burn-up equation by Krylov subspace
  • Numerical calculating method for accelerated solution of burn-up equation by Krylov subspace
  • Numerical calculating method for accelerated solution of burn-up equation by Krylov subspace

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

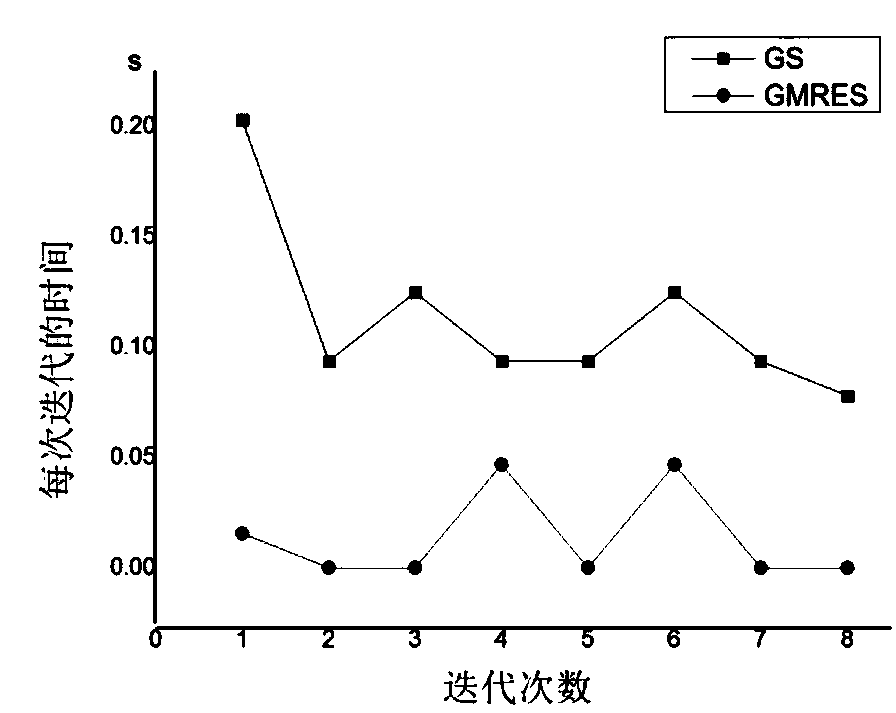
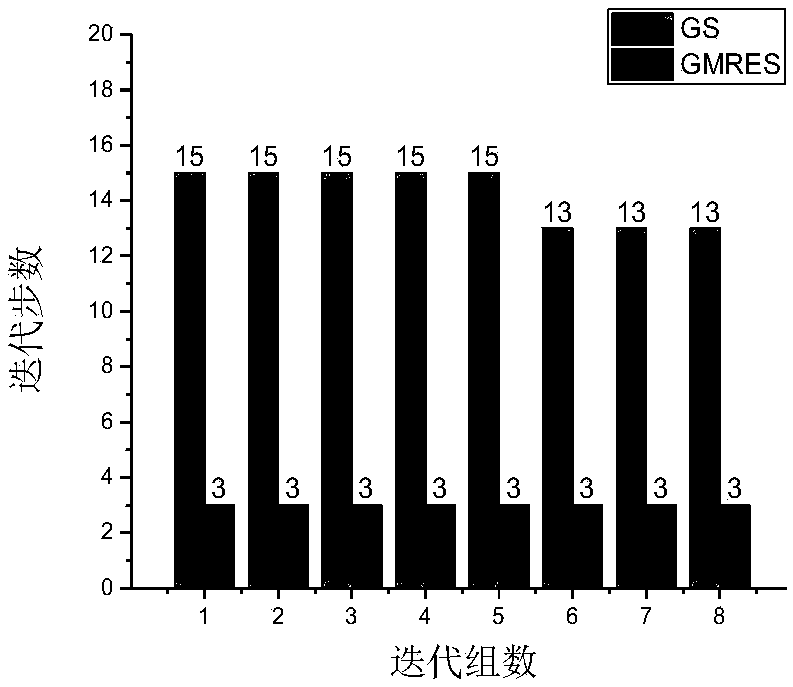
[0055] In a burnup step where the neutron flux remains constant, a new type of Krylov subspace is used to speed up the solution of the burnup equation. In order to accelerate the matrix exponential rational expansion algorithm in the process of solving the fuel consumption, the new Krylov subspace method—generalized residual method [2] Coupled with the original matrix exponential rational expansion method, the fuel consumption solution speed is improved on the premise of ensuring a certain accuracy requirement. It is mainly to project an n-dimensional burnup matrix and initial nuclide concentration onto an m-dimensional subspace, and then find the optimal solution in this subspace. Since the dimension m of the subspace is much smaller than the dimension n of the burnup matrix itself, the calculation amount is greatly reduced when solving, and the calculation speed is greatly improved. The algorithm is further optimized, including the application of matrix offset technology, pre...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a numerical calculating method for accelerated solution of a burn-up equation by the Krylov subspace, based on a rationally developed matrix index method, the burn-up solutionspeed is improved on the premise of ensuring a certain precision requirement by coupling a new Krylov subspace method, namely, a generalized minimum residual method. The main purpose is to project ann-dimensional burn-up matrix and an initial nuclide concentration onto an m-dimensional subspace, and then find the optimal solution in this subspace. Since the dimension m of the subspace is much smaller than the dimension n of the burn-up matrix itself, the amount of calculation is greatly reduced during solution, and the calculating speed is greatly improved.

Description

technical field [0001] The invention relates to the field of nuclear engineering, in particular to a calculation method for a physical burnup equation of a nuclear reactor. Background technique [0002] Burnup calculation is to calculate the composition of nuclear fuel, which is of great significance to the operation, cooling and radioactive protection of nuclear power plants. This calculation has relatively high requirements on calculation speed and accuracy. At present, there are two main methods to calculate the burnup: the first is to solve the burnup chain, such as the TTA method. This method has relatively high calculation accuracy, but relatively low efficiency, and is suitable for the calculation of a single nuclide. Another method is to solve the fuel consumption equation in the form of a matrix, and use the matrix exponential method to solve it quickly. This method has relatively high computational efficiency, but the numerical results are greatly affected by the ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06F17/50
CPCG06F30/20
Inventor 蔡杰进李学仲
Owner SOUTH CHINA UNIV OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com