Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

A new weno format construction method under the framework of trigonometric functions

A technology of trigonometric functions and construction methods, applied in complex mathematical operations, special data processing applications, design optimization/simulation, etc., can solve problems such as difficult implementation and complex calculations, achieve small truncation errors, simplicity and easier expansion, and avoid non-physical oscillating effect

Active Publication Date: 2022-04-01
NANJING UNIV OF AERONAUTICS & ASTRONAUTICS
View PDF3 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Zhu and Qiu proposed a method to reconstruct the WENO format with trigonometric polynomials in 2010, but the calculation is complicated and difficult to implement

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • A new weno format construction method under the framework of trigonometric functions
  • A new weno format construction method under the framework of trigonometric functions
  • A new weno format construction method under the framework of trigonometric functions

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

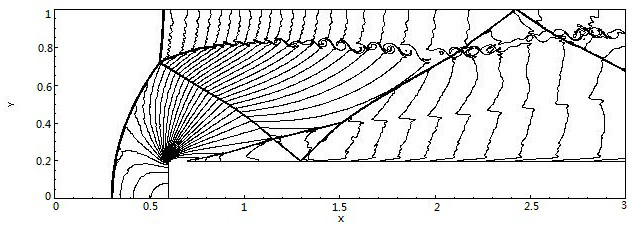
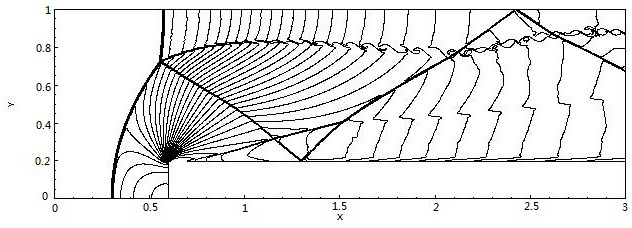
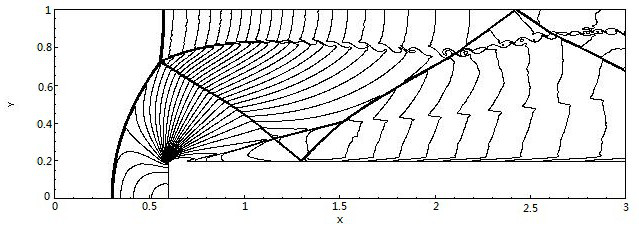
[0112] Embodiment 1, step problem. This problem is a classic example proposed by Emery in 1968 to test the nonlinear hyperbolic conservation law scheme. The initial data is that the Mach number of the horizontal incoming flow is 3, the density is 1.4, the horizontal velocity is 3, the vertical velocity is 0, the pressure is 1, the pipeline area is [0,3]×[0,1], and the distance from the left boundary is 0.6 There is a step with a height of 0.2, and the step extends to the end of the pipe. The upper and lower boundaries are reflection boundaries, the left boundary is the incoming flow boundary, and the right boundary is the outflow boundary. Figure 1a-1c The density contour plot at t=4 is given.

Embodiment 2

[0113] Embodiment 2, double Mach reflection problem. This problem describes the changes that occur when a strong shock wave at an angle of 60° to the x-axis hits a reflecting wall, and the incoming flow is a strong shock wave with a Mach number of 10. The calculation area is [0,4]×[0,1]. Region bottom from The reflective boundary condition starts at y=0, and the other bottom boundaries (from x=0 to That part) is the wavefront condition. Figure 2a-2c The density contour map in the area [0,3]×[0,1] at t=0.2 is given.

Embodiment 3

[0114] Embodiment 3, the problem of mutual interference between shock wave and eddy current. The shock wave with a Mach number of 1.1 is located at x=0.5 and is perpendicular to the x-axis. The initial state of the shock wave is The small eddy is located to the left of the shock and its center is at (x c ,y c )=(0.25,0.5). The eddy current can be regarded as the disturbance of the velocity, temperature and entropy of the mean flow, expressed as:

[0115]

[0116] where, τ=r / r c , ε=0.3, r c =0.05, α=0.204, γ=1.4, and the calculation area is [0,2]×[0,1]. Figures 3a-3c The pressure contour map in [0,1]×[0,1] area is given at t=0.35. Figures 4a-4c The pressure contour map in [0.4,1.45]×[0,1] area is given at t=0.6. Figures 5a-5c The pressure contour map in the [0,2]×[0,1] region is given at t=0.8.

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

A method for constructing a new WENO scheme under the framework of trigonometric functions. On the one hand, the weighted basic non-oscillating scheme constructed with trigonometric polynomials is easier to simulate wave or high-frequency oscillation problems than the classical basic non-oscillating scheme constructed with algebraic polynomials. The smooth region can obtain high-order numerical accuracy, and maintains the property of basically no oscillation at the shock wave and contact discontinuity; on the other hand, although the new TWENO format uses the same five-point information as the classic fifth-order WENO format, it can get lower global L 1 and L ∞ Norm truncation error. The linear weight adopted by the new TWENO format no longer needs to obtain the optimal solution through cumbersome numerical calculations, and can be set to any positive number that satisfies the sum to be one. Compared with the classic WENO format, it is simpler, more robust, and easier Generalized to high-dimensional space. The new TWENO scheme effectively simulates several classical Euler problems numerically, and fully verifies the effectiveness.

Description

technical field [0001] The invention belongs to the technical field of computational fluid dynamics engineering, and in particular relates to a new WENO format construction method under the trigonometric function framework. Background technique [0002] Flow field problems often arise in engineering applications, such as aerodynamic systems and shallow water modeling. Therefore, developing robust, accurate, and efficient numerical simulation methods to solve such problems is of great importance and has attracted the interest of many researchers. In 1959, Godunov proposed a first-order precision numerical simulation scheme for solving flow field problems. The numerical simulation method with first-order accuracy will not cause non-physical numerical oscillations when capturing shock waves, but it will over-smooth strong discontinuities, and often strong discontinuities are of great significance to the follow-up research of the problem, so it is necessary to introduce high-pr...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G06F30/23G06F17/15
CPCG06F17/15G06F30/23G06F2111/10
Inventor 王延萌朱君熊良林
Owner NANJING UNIV OF AERONAUTICS & ASTRONAUTICS
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com