A Quantization Method for Deep Neural Networks Based on Elastic Significant Bits
A technology of deep neural network and quantization method, which is applied in the field of deep neural network quantization based on elastic effective bits, can solve the problems of difficult step function, decreased precision, and reduced computational efficiency of quantized models, achieving efficient multiplication calculations, improving accuracy, The effect of low quantization loss
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment 1
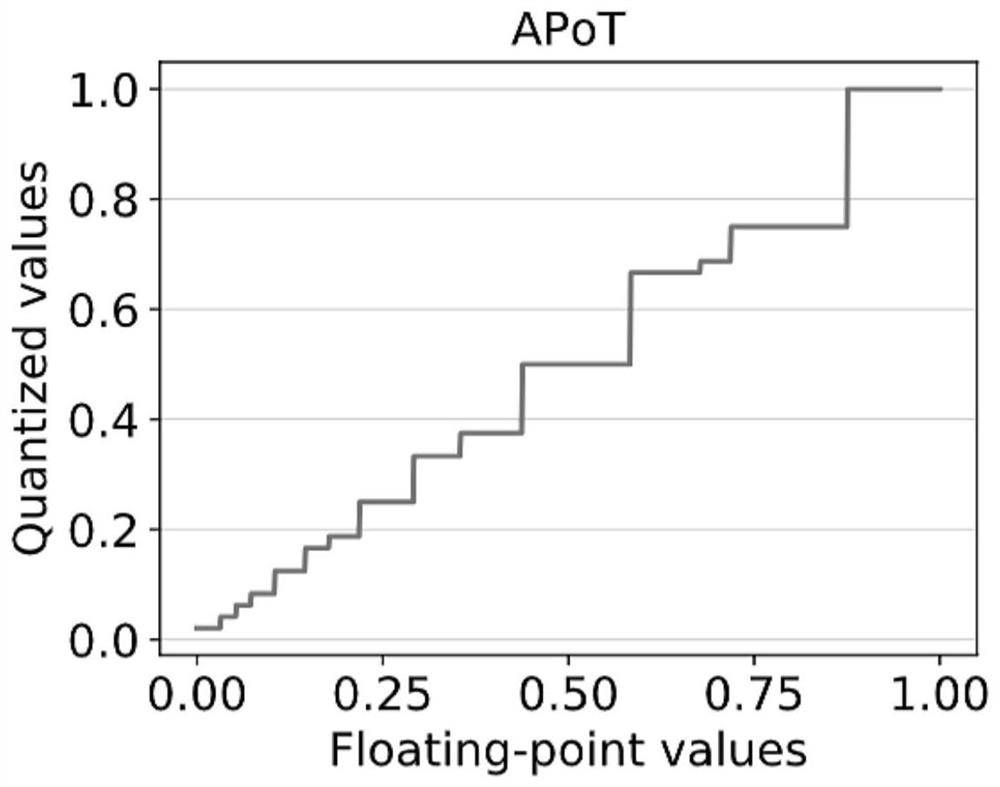
[0040] Embodiments of the present invention provide a deep neural network quantization method based on elastic effective digits, which quantizes fixed-point numbers or floating-point numbers into quantized values with elastic effective digits, and discards redundant mantissa parts. The flexible significant bit is reserved from the most significant bit, and there are a limited number of significant bits.
[0041] For a given data v, from the position of its most significant bit, specify k+1 significant bits, expressed as follows:
[0042]
[0043] Among them, the part from (n-k) to n is the effective part reserved, and the part from 0(-∞) to (n-k-1) is the mantissa part that needs to be rounded; quantization of fixed-point or floating-point numbers:
[0044] P(v)=R(v>>n-k)<
[0045] Among them, >> and << are shifting operations, and R() is a rounding operation.
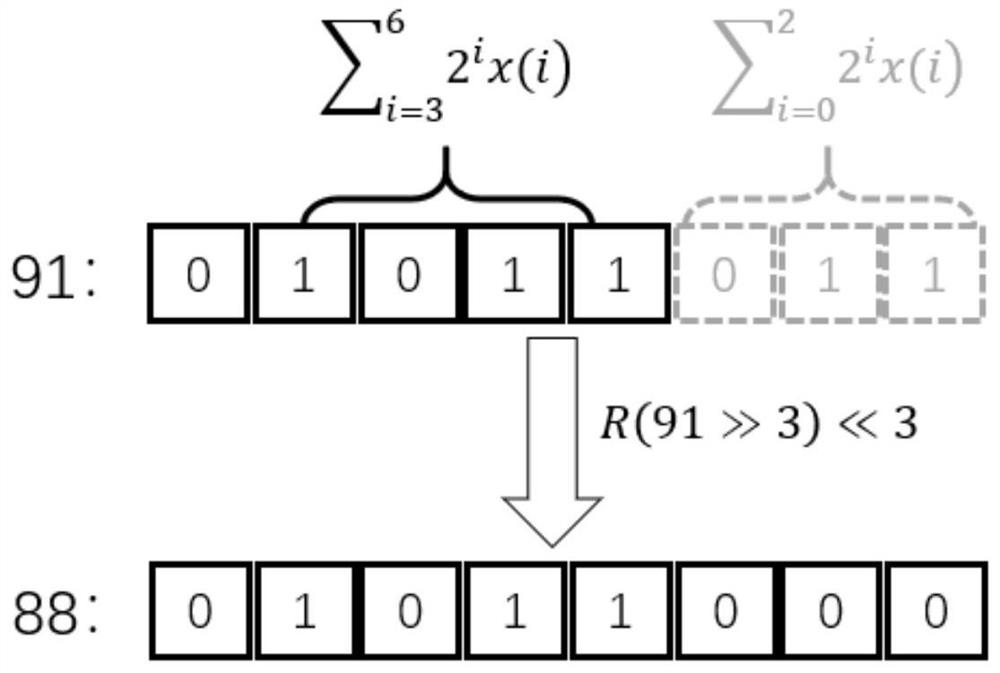
[0046] Such as image 3 As shown, in this embodiment, 91 is quantized, and the flexible valid bits are s...
Embodiment 2
[0049] Embodiments of the present invention provide a deep neural network quantization method based on elastic effective digits, which quantizes fixed-point numbers or floating-point numbers into quantized values with elastic effective digits, and discards redundant mantissa parts. The flexible significant bit is reserved from the most significant bit, and there are a limited number of significant bits.
[0050] For a given data v, from the position of its most significant bit, specify k+1 significant bits, expressed as follows:
[0051]
[0052] Among them, the part from (n-k) to n is the effective part reserved, and the part from 0(-∞) to (n-k-1) is the mantissa part that needs to be rounded; quantization of fixed-point or floating-point numbers:
[0053] P(v)=R(v>>n-k)<
[0054] Among them, >> and << are shifting operations, and R() is a rounding operation.
[0055] Such as Figure 5 As shown, in this embodiment, 92 is quantized, and the flexible valid bits are ...
Embodiment 3
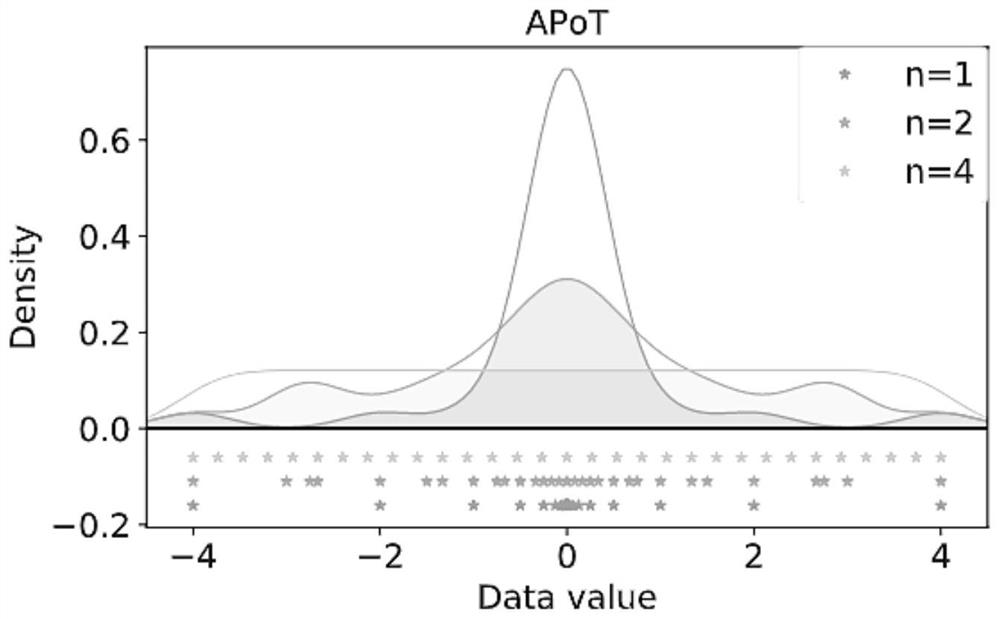
[0058] It is to quantitatively evaluate the distribution difference between the quantitative value and the original data by means of a feasible solution:
[0059] The quantization weight is W, which is sampled from random variables t~p(t), and the set of all quantization values is Q, and the distribution difference function is defined as follows:
[0060]
[0061] s.t.S=(q-q l ,q+q u ]
[0062] where (q-q l ,q+q u ] represents the range of continuous data that can be projected onto q-values, the range is centered at q, and q 1 and q u Indicates its floating range. Its solution diagram is as follows Figure 7 shown. Distribution differences can be used to evaluate optimal quantification at different elastic significands.
[0063] Input: There is a DNN weight w sampled from the standard normal distribution N(0, 1) f , it needs to be quantized to a low-precision value of 4 bits;
[0064] Output: the optimal effective number of digits, quantized weight w q .
[0...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com