[0100] Secondly, the specific embodiment of the invention is as follows:
[0101] A distributed projection method based on variance reduction technology considering communication delay includes the following steps:
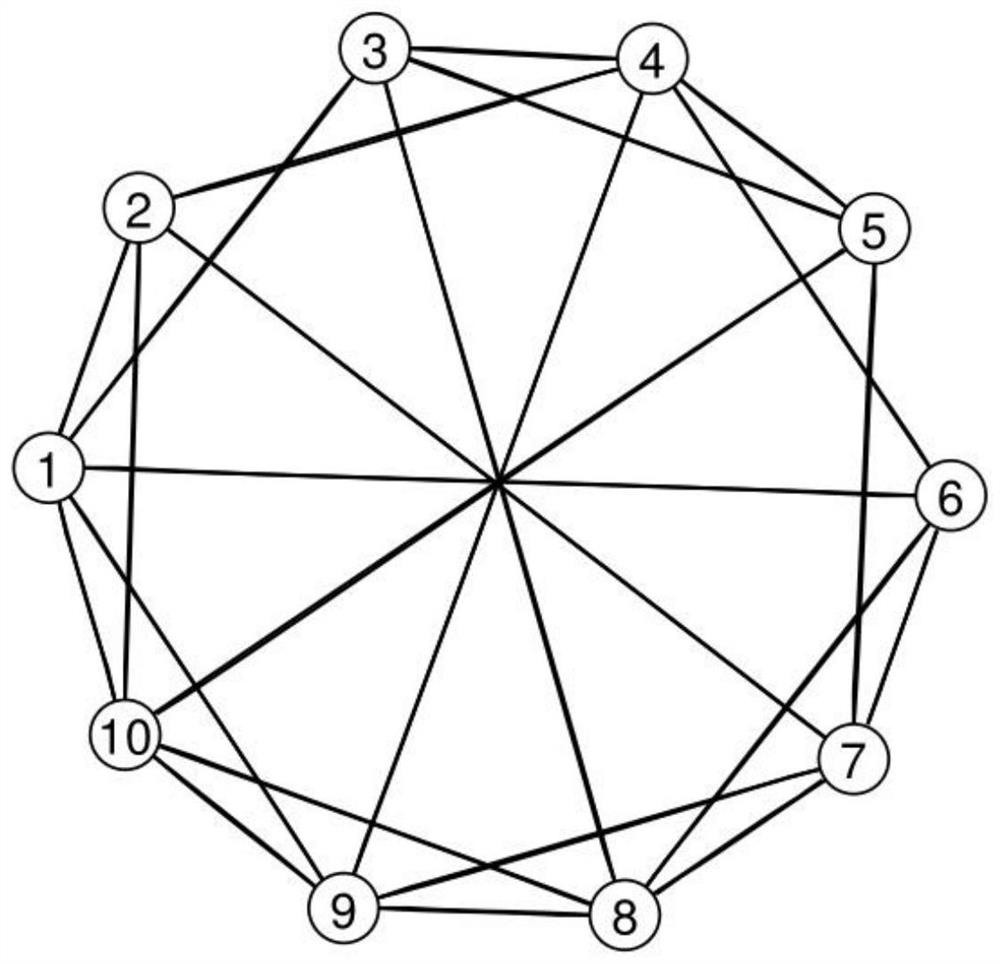
[0102] 1, putting forward a primal optimization problem model (1) for a multi-intelligent system with local set constraints and local equality constraints;
[0103] 2, equivalently converting the original optimization problem model (1) obtained in step 1 into a convex optimization problem model (2) which is convenient for distribution and processing;
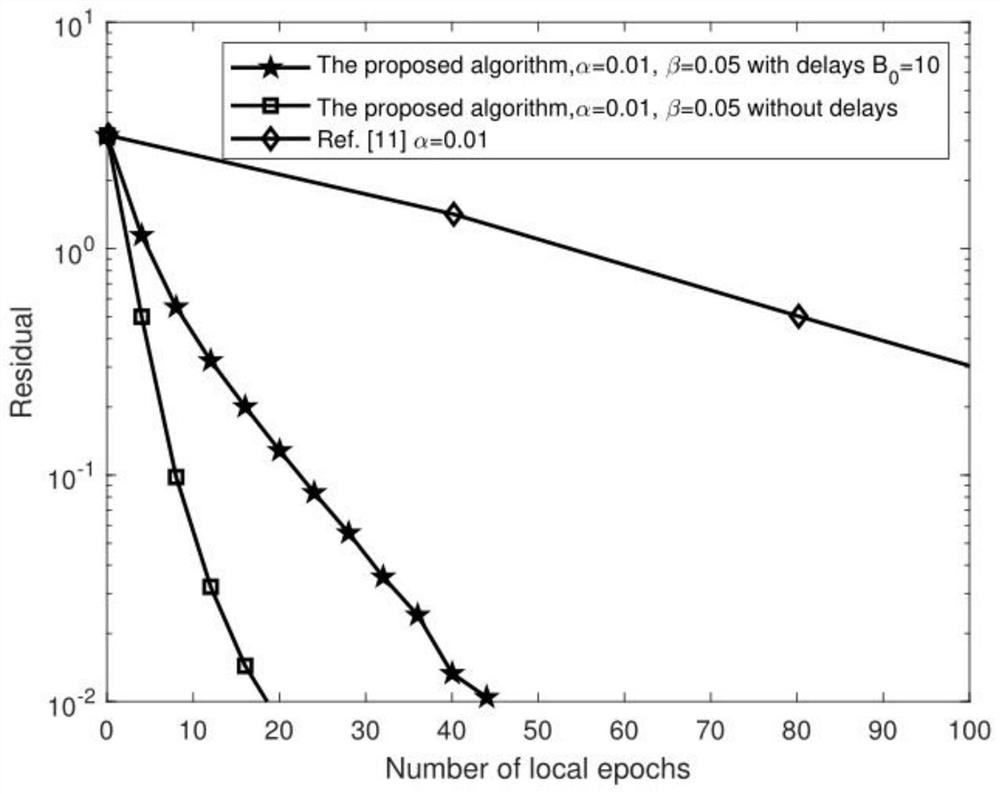
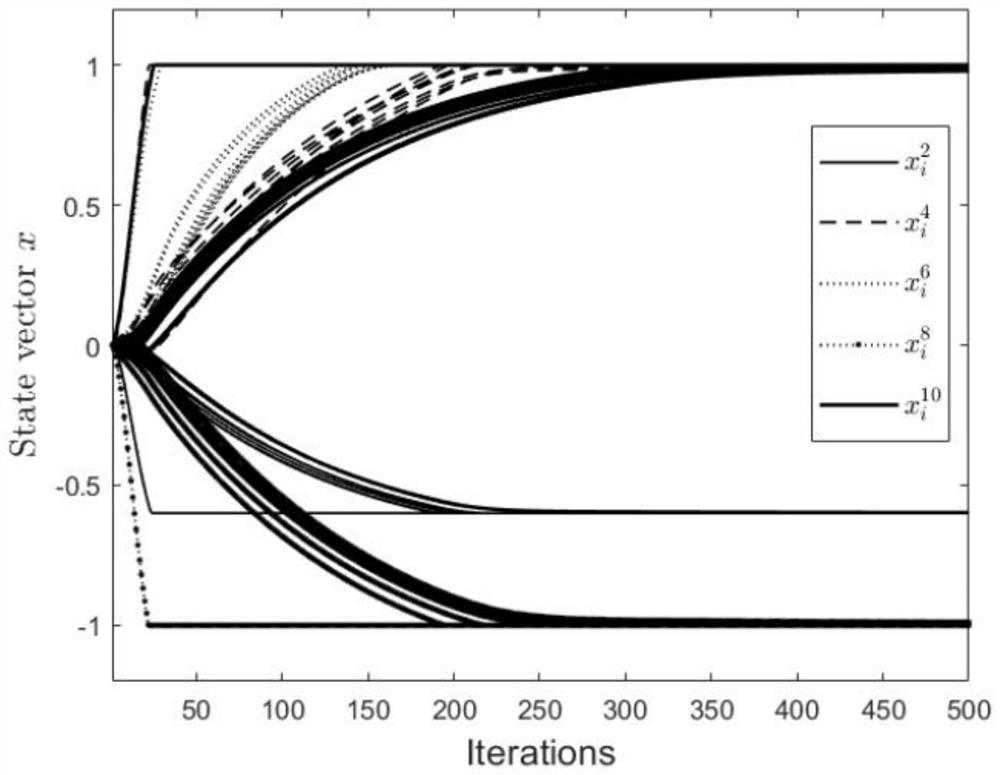
[0104] 3. Propose a distributed projection algorithm based on variance reduction technology. (3) Solve the constrained convex optimization problem model (2), that is, use the local random average gradient to estimate the local full gradient without bias, so as to reduce the heavy computational burden caused by calculating the full gradient of all local objective functions in each iteration.
[0105] 4, analyzing the convergence of the distributed projection algorithm (3) based on variance reduction technology proposed in step 3;
[0106] The concrete construction process and form of the original optimization problem model (1) in step 1 are as follows:
[0107] Firstly, define an agent cluster V = {1, …, m}, a communication network edge set. And adjacent moment array. Undirected communication network based on And the simple network g has no self-circulation;
[0108] When the agent (i,j)∈E, a ij ＝a ji 0, otherwise a ij ＝a ji ＝0；
[0109] The degree of agent I is expressed as
[0110] For diagonal matrix d = diag {d 1 ,d 2 ,...,d m }, the Laplace matrix of the undirected network G is defined as
[0111] If the undirected network G is connected, then Laplacian matrix Is symmetrical and semi-positive;
[0112] Secondly, the specific form of the original optimization problem model (1) is as follows
[0113]
[0114] In the above formula, the objective function Indicates the sample to be processed in a practical problem, and the Table decision vector, q i Indicates the total number of local problems assigned to agent I;
[0115] At the same time, the local objective function is further decomposed into among h∈{1,...,q i } is a sub-function of the h-th local objective function;
[0116] Based on the above formula, define Is a closed convex set, and the intersection x is non-empty, define a column full rank matrix. and The optimal solution of constrained convex optimization problem (1) is defined as
[0117] The specific form of the convex optimization problem model (2) in step 2 is as follows:
[0118]
[0119] Where x i Agent I pairs the decision vectors. Estimated value of;
[0120] Matrix b is defined as a diagonal matrix with full rank, and the diagonal elements are {B 1,...,B m }, that is
[0121] Stacking vector
[0122] make Cartesian product;
[0123] make
[0124] q i The maximum and minimum values of are expressed as Q respectively. max And q min (where q min ≥1, that is, each agent processes at least one sample);
[0125] According to the above statement, λ can be obtained. min (B T B)q min ＞0；
[0126] Based on the above convex optimization problem model (2), the following assumptions and definitions are made:
[0127] Hypothesis 1: Each local sub-objective function f i h All of them are strongly convex and have Lipschitz continuous gradients. That is, for all i∈V, H ∈ {1, ..., Q. i }, and Have the following formula:
[0128]
[0129]
[0130] Where 0 < μ≤ L f;
[0131] Then, under the condition that hypothesis 1 is established, the global optimal solution of constrained convex optimization problem (2) is unique and expressed as
[0132] 2: The undirected network G is connected;
[0133] Hypothesis 3: For and exist
[0134]
[0135] Among them b 0 Is a positive integer.
[0136] 1: Define global vector to collect local variable X. i,k ,y i,k ,w i,k ,g i,k and As follows:
[0137]
[0138]
[0139]
[0140]
[0141]
[0142] And global vector X. k And W. k Partial version:
[0143]
[0144]
[0145] Then, at the k-th iteration, the communication delay I,j∈V, determined by agent I and agent J at the same time, therefore, the global delay vector x k [i] and w k [i] is only held by agent I.
[0146] The specific iterative process of the distributed projection algorithm (3) based on variance reduction technology in step 3 is as follows:
[0147] Initialization: for all agents i∈V, initialize X i,0 ,
[0148] Setting: k = 0
[0149] For agent I = 1, ..., m, execute
[0150] 1: from the set {1,...,q i } to choose any sample.
[0151] 2. Calculate the local random average gradient as follows
[0152]
[0153] 3: Settings And store.
[0154] 4: Update the variable x i,k+1 as follows
[0155]
[0156] 5: Update the variable Y. i,k+1 as follows
[0157] y i,k+1 ＝y i,k +B i x i,k+1 -b i
[0158] 6: Update the variable w i,k+1 as follows
[0159] w i,k+1 ＝w i,k +βx i,k+1
[0160] End of cycle
[0161] Set k = k+1, and repeat the above cycle until the stop condition is met;
[0162] Wherein, the Is a sub-function of the local objective function. h∈{1,...,q i } at the iteration value of the kth iteration, Represents an n-dimensional real column vector.
[0163] Said The iteration rules of are as follows:
[0164]
[0165] At iteration k, for agent I, a local random average gradient is defined:
[0166]
[0167] among The following iteration can be used for calculation:
[0168]
[0169] Ling f k Representing the σ algebra generated by the local random average gradient in iteration k, the following equation can be obtained:
[0170]
[0171] The convergence analysis process in step 4 is as follows:
[0172]First of all, in the practical application process, this embodiment adopts the following seven lemmas in the convergence analysis: Lemma 1: For any non-empty closed convex set X, the following two inequalities hold.
[0173]
[0174]
[0175] In which p X [] is a projection operator;
[0176] Lemma 2: If it exists and The global optimal solution of constrained convex optimization problem (2) is obtained under the condition that the first assumption is established. Only exists, and there are:
[0177]
[0178] Where the constant step alpha > 0 and the parameter beta > 0;
[0179] Lemma 3: Under the assumption 1-2, consider the sequence generated by distributed projection algorithm (3) based on variance reduction technology. And {g k } k≥0 , for have
[0180]
[0181] In which the auxiliary sequence {p k } k≥0 Is defined as:
[0182]
[0183] Sequence {p k } k≥0 It is assumed to be non-negative under the condition that one is established;
[0184] Lemma 4: Considering the distributed projection algorithm (3) and sequence (13) based on variance reduction technology under the condition of hypothesis 1, for have
[0185]
[0186] Lemma 5: Consider the global vector V under the condition that hypothesis 3 holds. k ＝[(v 1,k ) T ,...,(v m,k ) T ] T And its delayed version v. k [i], there are:
[0187]
[0188] among For a given sequence {v t } t≥0 , we give
[0189]
[0190] Here, l and d are two non-negative scalars; Then, the The superposition of k from 0 to n can be obtained.
[0191]
[0192] Lemma 6: Considering the distributed projection algorithm (3) based on variance reduction technology under the conditions of assumptions 1-3, the following inequalities hold.
[0193]
[0194] among And w = I-α l, φ and η are positive constants;
[0195] The concrete proof process of the above conclusion is as follows:
[0196] According to definition 1, we give the shorthand form of distributed projection algorithm (3) based on variance reduction technology as follows:
[0197]
[0198] y i，k+1 ＝y i，k +Bix i，k+1 -b i (9b)
[0199] w i，k+1 ＝w i，k +βx i，k+1 (9c)
[0200] among And v i，k Defined as follows:
[0201]
[0202] According to (9a), we have:
[0203]
[0204]
[0205] Among them, the inequality uses the following formula:
[0206] (I) take note of x k+1 ＝P X [v k ], then according to Lemma 1, the following formula holds:
[0207]
[0208] among and
[0209] (ii) Similar to [12], we have
[0210]
[0211] Next, continue the analysis.
[0212]
[0213] Where η sum Is a positive constant, the first inequality applies Young's inequality, and the second inequality uses that the function f is strongly convex and has Lipschitz continuous gradient. Substituting the result of (27) into (24) can get:
[0214]
[0215] Next to 2α(x k+1 -x * ) T B T B(x k+1 -x k ) for processing:
[0216]
[0217] Substitute the result of formula (29) into formula (28), and take the expectation to get:
[0218]
[0219]
[0220] According to formula (8), we know that Therefore, we are going to Carry out treatment
[0221]
[0222] In which p kIn the definition (13), the first equation in (31) uses the standard variance decomposition E [|| A-E [A | F. k ]|| 2 |F k ]＝E[||a|| 2 |F k ]-||E[a|F k ]|| 2 The inequality uses the strong convexity sum of f. The continuity of Lipshits. Next, substituting the conclusion of (31) into (30) can get:
[0223]
[0224] Next, we will introduce an important relation, Where v is a semi-positive definite matrix. According to this relation, we can get the following three formulas:
[0225]
[0226] Finally, substitute the result of formula (33) into formula (32).
[0227] Lemma 7: Under the condition that hypothesis 3 holds, the following two inequalities hold.
[0228]
[0229]
[0230] In which ξ 1 ，ξ 2 Are two arbitrarily positive constants; It is worth noting that when the undirected network is determined, It will be determined accordingly.
[0231] Conclusion The specific proving process is as follows:
[0232] Let's first prove (19a) in Lemma 7.
[0233]
[0234] The second inequality uses Lemma 5, the last inequality uses Young's inequality, and ξ 1 Is a positive constant; The proof process of (19b) is similar to that of (19a), so it will not be repeated here;
[0235] Secondly, for the convenience of analysis, the following definitions are made:
[0236] 2: For 0 < α < 1/λ max (l), define a semi-positive definite matrix p as:
[0237]
[0238] Where W = I-α L is a positive definite matrix, so there is:
[0239]
[0240] In which vector And u * ＝[(x * ) T ,(y * ) T ,(w * ) T ] T;
[0241] Then the following conclusions can be obtained by combining assumptions 1-3 and definitions 1-2:
[0242] Under the assumption of 1-3, consider distributed projection algorithm (3) based on variance reduction technology and U in definition 2. k And the definition of U*, if the parameters η, φ and ξ satisfy:
[0243]
[0244] 0＜φ＜2μ (21b)
[0245]
[0246] Then, the constant step alpha and the algorithm parameter beta satisfy:
[0247]
[0248]
[0249] Then the sequence {U k } k≥0 Is bounded and convergent, then the sequence {x k } k≥0 Is the only one that converges to X. * Yes.
[0250] The specific certification process is as follows:
[0251] For α > 0 and β > 0, substituting the result of Lemma 7 into Lemma 6 can get:
[0252]
[0253]
[0254] among Is defined in Theorem 6. Next, according to Lemma 4, we put c(E[p k+1 |F k ]-p k ) added to (35)
[0255] Get both ends:
[0256]
[0257] According to Lemma 3, we know the sequence P. k ≥0； Therefore, if η > 2l f [L f q max +q min (L f -μ)]/λ min (B T B)q min And 4αq max L f /η≤c, then (36) can be rewritten as:
[0258]
[0259] According to definition 2, if 0 < α < 1/λ max (L), and 0 < β < 1, we have
[0260]
[0261] To deal with the first item at the right end of the inequality sign in (38), we set ξ below. 1 ＝ξ 2 = ξ, 0 < φ < 2μ, and 0 < ξ Based on this definition, we can rewrite formula (38) as:
[0262]
[0263] Sum (39) about k from 0 to n to get:
[0264]
[0265] Under conditions (21) and (22), we define a semi-positive definite matrix.
[0266]
[0267] Therefore, inequality (40) can be rewritten as:
[0268]
[0269] When n approaches infinity, we have
[0270]
[0271] The formula shows that the right side of formula (39) is summable. Therefore, the sequence On inner product P Is quasi Fejér monotone; We can get the sequence directly. Is bounded and convergent; Therefore, the sequence {U k } k≥0 Is bounded and convergent; Finally we can get the sequence {x k } k≥0 Convergence to x *; Under the assumption that 1 holds, we know the global optimal solution X. * Is the only one that exists.
