Novel WENO-format high-precision fractional derivative approximation method

A fractional derivative, high-precision technology, applied in electrical digital data processing, complex mathematical operations, CAD numerical modeling, etc., can solve problems such as complex and cumbersome calculation processes

Pending Publication Date: 2021-02-02
NANJING UNIV OF AERONAUTICS & ASTRONAUTICS
View PDF0 Cites 2 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, in the implementation process of WENO6 format, the calculation process of lin...

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Novel WENO-format high-precision fractional derivative approximation method
  • Novel WENO-format high-precision fractional derivative approximation method
  • Novel WENO-format high-precision fractional derivative approximation method

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0125] Embodiment 1: The following fractional differential equation is given

[0126]

[0127] The initial conditions are:

[0128]

[0129] The boundary conditions are:

[0130] u(-L,t)=1, u(L,t)=0; (19)

[0131] in V=0.5 and L=1 or 10.

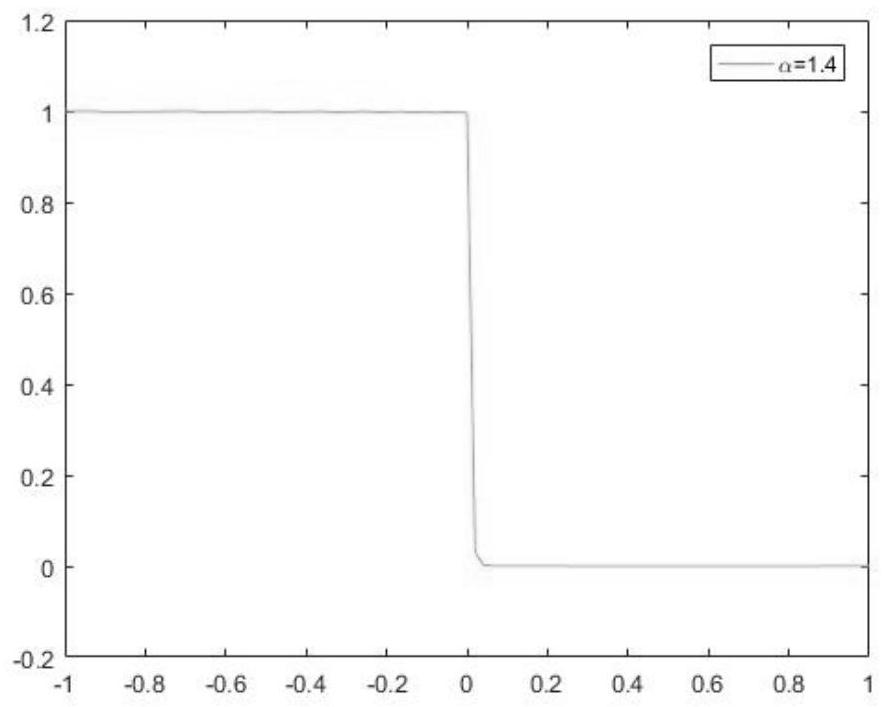
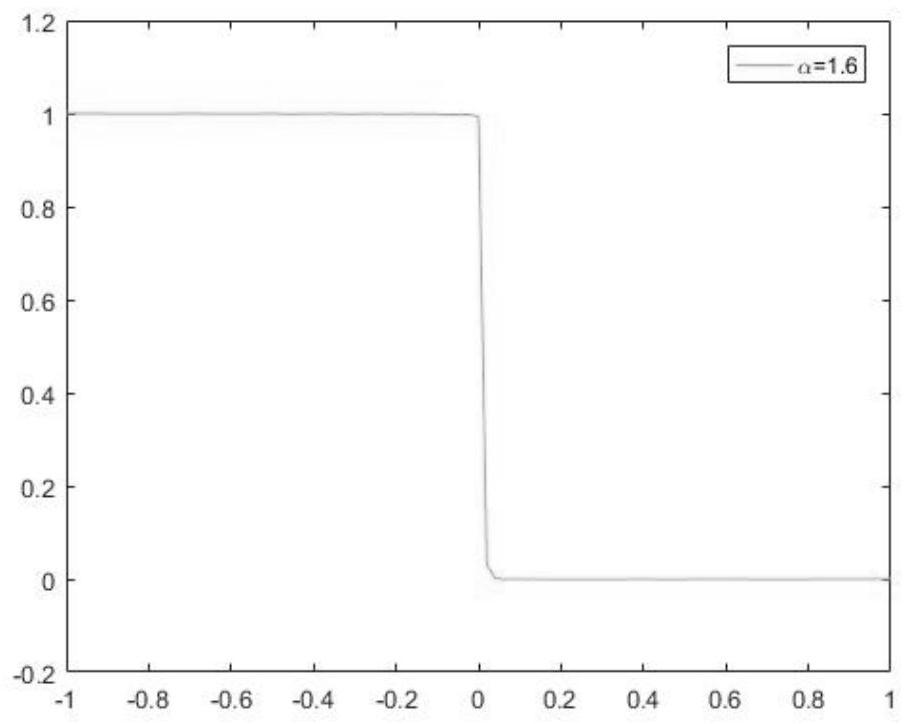
[0132] exist Figure 1-12 In the numerical simulation of , take D=0.02, L=1, h=2 / N, grid points N=100, time step τ=0.4h 2 , Figure 1-4 , Figure 5-8 , Figure 9-12 Numerical solutions of fractional derivatives of different orders α=1.2, 1.4, 1.6, 1.8 at T=0.001 are given respectively, and it can be noticed that the sharp transition is preserved for different α numerical simulations.

[0133] exist Figure 13-15 In the numerical simulation of , take D=0.2, L=10, h=20 / N, grid points N=200, time step τ=0.4h 2 , Figure 13-15 Numerical solutions of fractional derivative α=1.8 at T=1,2,3 are given.

[0134] exist Figure 16-18 In the numerical simulation of , take D=0.2, L=10, h=20 / N, grid points N=200, time step τ=0.3h 1.8 ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

PUM

No PUM Login to view more

Abstract

The invention discloses a novel WENO-format high-precision fractional derivative approximation method. The method comprises the steps: decomposing a Caputo fractional derivative in a fractional differential equation into a classical second derivative and a weak singular integral in a Cartesian coordinate system, discretizing the classical second derivative by using a novel WENO format, and solvingthe weak singular integral by using Gauss-Jacobi quadra-ture; for a time derivative in an equation, using a three-order TVD Runge-Kutta discrete formula to discretize a semi-discrete finite difference format into a space-time full-discrete finite difference format, wherein the space-time full-discrete finite difference format is an iterative formula about a time layer, and an initial state valueis known; and according to the space-time full-discrete finite difference format, solving an approximate value of a next time layer through an iterative formula, and sequentially acquiring a numericalsimulation value in a calculation region at the end moment. The method can achieve six-order precision in the smooth area of a solution, and can keep the property of basically no oscillation in a discontinuous strong interruption area.

Description

technical field [0001] The invention belongs to the technical field of computational fluid dynamics engineering, and in particular relates to a novel WENO format high-precision fractional derivative approximation method. Background technique [0002] High-precision finite-difference and finite-volume WENO schemes are used to solve piecewise smooth solutions with discontinuities. Liu, Osher and Chan et al. first proposed the first third-order finite volume WENO scheme in 1994, which improved the utilization of calculation results and improved the r-order precision ENO scheme to r+1-order numerical precision. In 1996, Jiang and Shu further improved the construction strategy of the high-order finite-difference WENO scheme, so that the numerical accuracy can be increased to the 2r-1 order numerical accuracy, and a new construction framework for smoothing factors and nonlinear weights was designed. [0003] In the implementation process of the classic WENO format, the linear wei...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

Application Information

Patent Timeline
no application Login to view more
IPC IPC(8): G06F17/13G06F30/23G06F30/28G06F113/08G06F119/14G06F111/10
CPCG06F17/13G06F30/23G06F30/28G06F2111/10G06F2113/08G06F2119/14
Inventor 张燕朱君
Owner NANJING UNIV OF AERONAUTICS & ASTRONAUTICS
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Try Eureka
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap