Check patentability & draft patents in minutes with Patsnap Eureka AI!

Method for correcting non-orthogonal coordinate axes of three-dimensional coordinate system

A calibration method and coordinate system technology, applied to measurement devices, instruments, navigation through velocity/acceleration measurement, etc., can solve the problem that the external signal source cannot be covered, and achieve the effect of mutual orthogonality

Inactive Publication Date: 2021-02-12
博观创新(上海)大数据科技有限公司
View PDF0 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

This is unsatisfactory in many practical application scenarios, such as underground mining, underground engineering construction, underground drilling measurement and control, underground pipeline detection, subways, tunnels and underwater engineering, underwater detection and measurement and control and other hidden scenarios, external signal sources cannot cover

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method for correcting non-orthogonal coordinate axes of three-dimensional coordinate system
  • Method for correcting non-orthogonal coordinate axes of three-dimensional coordinate system
  • Method for correcting non-orthogonal coordinate axes of three-dimensional coordinate system

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

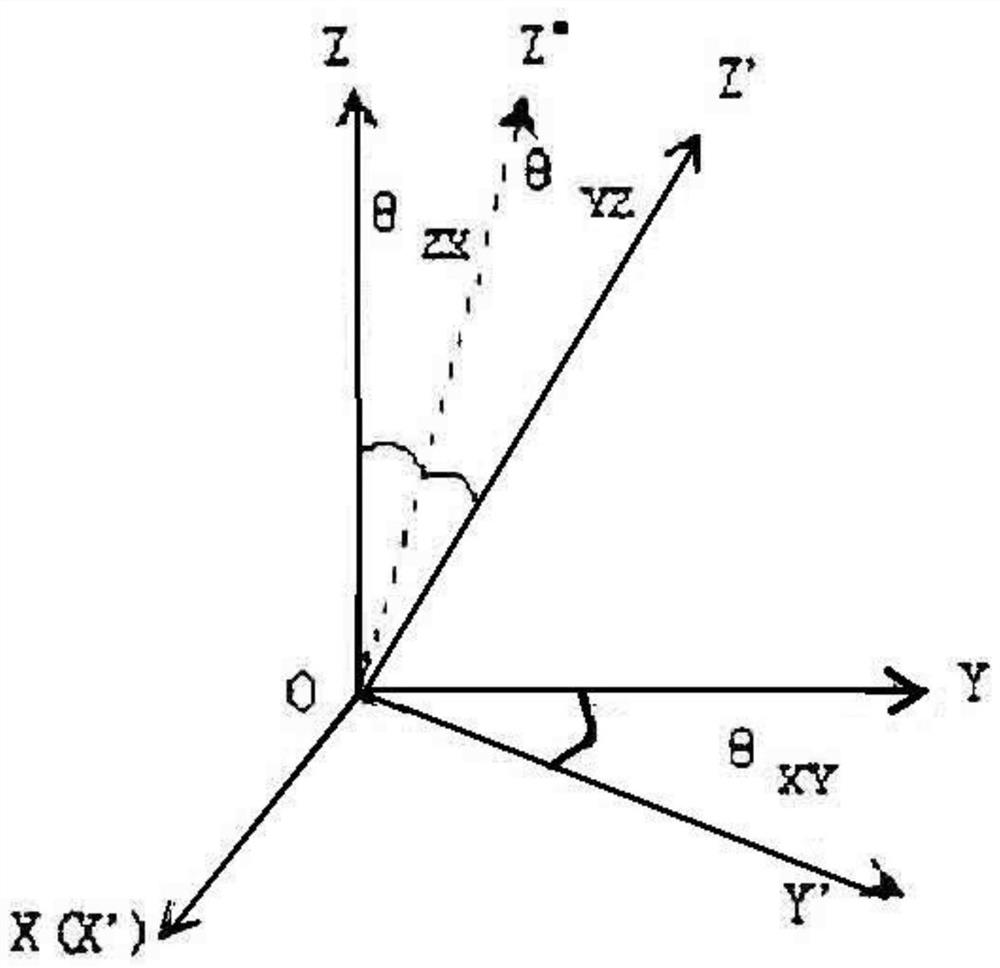
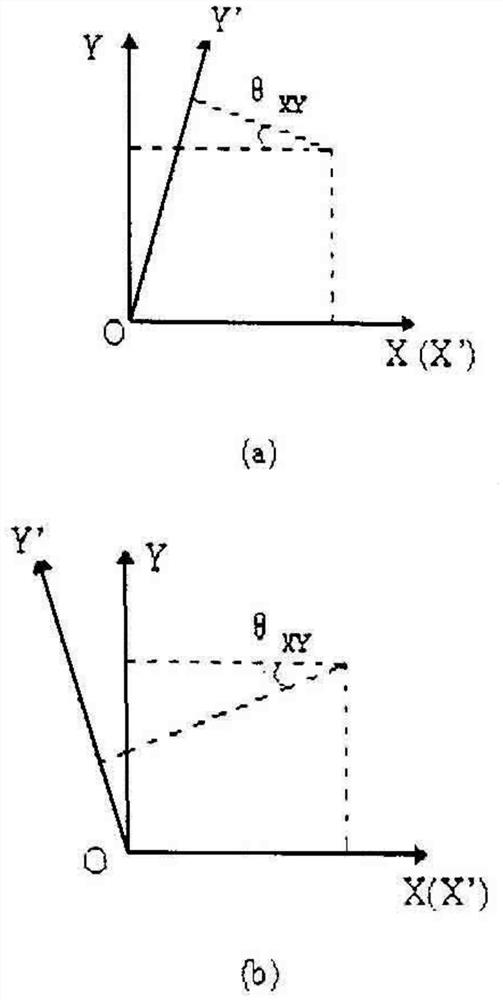
[0025] In the plane coordinate system, let the X-axis and the Y-axis be an orthogonal coordinate system, and the coordinates are x, y; the X' axis and the Y' axis are a non-orthogonal coordinate system, and the coordinates are x', y'. When the X axis coincides with the X' axis, the non-orthogonal angle between the Y' axis and the X axis or X' axis is θ XY ,exist figure 1 (a), figure 1 (b) is two non-orthogonal cases.

[0026] Depend on figure 1 (a):

[0027]

[0028] Depend on figure 1 (b):

[0029] y'=(y-x'tanθXY )cosθ XY

[0030] (2) Because the non-orthogonal angle is very small, approximately: cosθ XY ≈1 sinθ XY ≈tanθ XY ≈θ XY , and ignoring the second-order infinitesimal, formula (1) and formula (2) can be simplified as:

[0031] y=y'-x'θ XY (3)

[0032] y=y'+x'θ XY (4)

[0033] In the three-dimensional orthogonal coordinate system, O-XYZ is the orthogonal index system, and O-X'Y'Z' is the actual non-orthogonal coordinate system. Taking the X axis as...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a method for correcting non-orthogonal coordinate axes of a three-dimensional coordinate system, and the method comprises the following steps: establishing a correction equation according to the relationship between coordinate vectors and non-orthogonal angles when the coordinate axes are orthogonal and non-orthogonal; determining an objective function for calculating a non-orthogonal angle according to a correction relation of multiple actual physical quantity measurement values of the transformation position; determining a non-orthogonal angle by solving the optimal value of the target function by applying an optimization technology variable rotation method; and correcting the non-orthogonality among the three-dimensional coordinate axes according to the determined non-orthogonality angle. The method is high in reliability and precision, and can effectively improve the non-orthogonal correction precision of the coordinate axis of the three-dimensional coordinate system.

Description

technical field [0001] The invention relates to the field of measuring spatial physical quantities with a three-axis orthogonal coordinate system, in particular to a method for correcting non-orthogonal coordinate axes of a three-dimensional coordinate system. Background technique [0002] With the development of intelligence and information technology, the application of mobile ranging and positioning technology has become more and more extensive. The mobile ranging and positioning system can be used to measure and locate people, events, objects, and equipment to meet the requirements of mobile office, transportation, logistics, tourism, land and resources survey, marine monitoring, engineering construction and monitoring, military and other industries. demand. [0003] Mobile ranging and positioning mainly include technologies based on mobile communication networks and mobile terminals. Their common feature is that they need external signal sources, such as mobile communi...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G01C21/16G01C21/20G01C25/00
CPCG01C21/16G01C21/20G01C25/005
Inventor 郭伟薇谷俊
Owner 博观创新(上海)大数据科技有限公司
Features
  • R&D
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com