Supercharge Your Innovation With Domain-Expert AI Agents!

Reverse time migration method and device based on finite element

A technology of reverse time migration and finite element, applied in the direction of measuring devices, seismology, instruments, etc., can solve problems such as large amount of calculation, low parallel efficiency, staying in two-dimensional model experimental research, etc., to achieve high precision and improve efficiency Effect

Pending Publication Date: 2021-04-30
CHINA PETROLEUM & CHEM CORP +1
View PDF3 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, the existing finite element-based prestack reverse time migration method has a huge amount of calculation and low parallel efficiency, which cannot meet the timeliness requirements of industrial applications, and is still in the experimental research stage for 2D models.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Reverse time migration method and device based on finite element
  • Reverse time migration method and device based on finite element
  • Reverse time migration method and device based on finite element

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

[0129] Preferred embodiments of the present application will be described in more detail below with reference to the accompanying drawings. Although preferred embodiments of the present application are shown in the drawings, it should be understood that the present application may be embodied in various forms and should not be limited to the embodiments set forth herein. Rather, these embodiments are provided so that this application will be thorough and complete, and will fully convey the scope of this application to those skilled in the art.

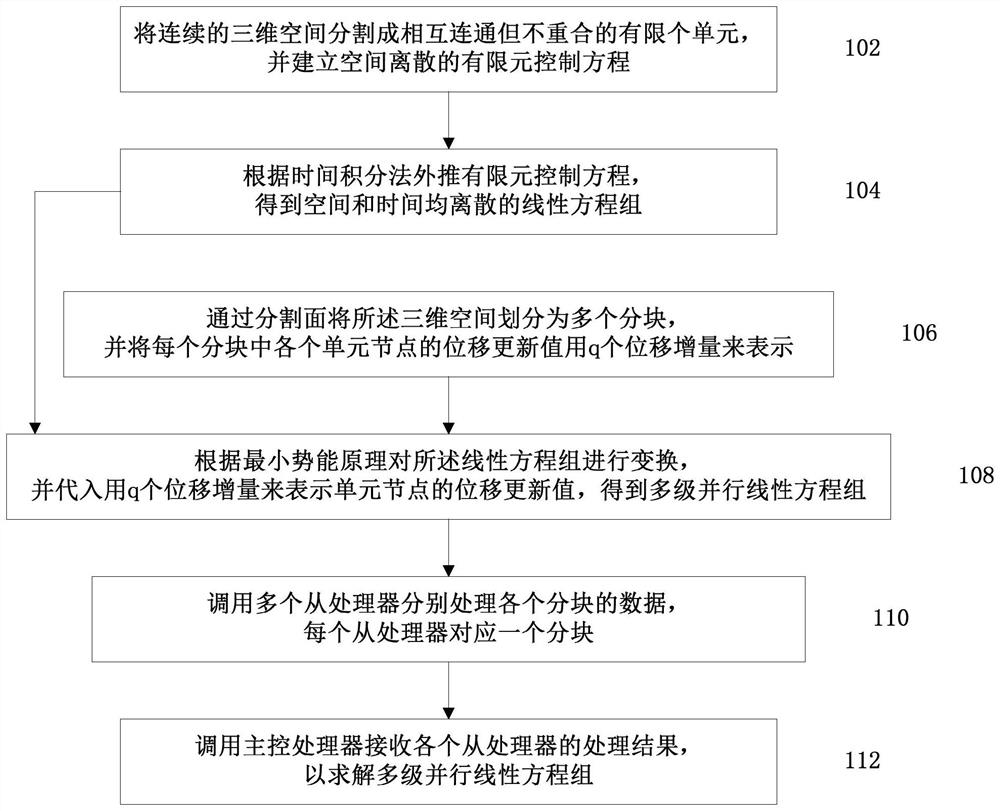
[0130] See figure 1 . figure 1 A flowchart showing a method for establishing a prestack time migration velocity field according to an embodiment of the present application. As shown in the figure, the method includes the following steps.

[0131] In step 102, the continuous three-dimensional space is divided into a finite number of interconnected but non-overlapping units, and a spatially discrete finite element governing equation i...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a reverse time migration method and device based on a finite element. The method comprises the following steps: establishing a finite element control equation; extrapolating a finite element control equation according to a time integral method to obtain a linear equation set; dividing the three-dimensional space into a plurality of blocks, and representing the displacement update value of each unit node in each block by q displacement increments; transforming the system of linear equations, and substituting q displacement increments to represent displacement update values of the unit nodes to obtain a multistage parallel system of linear equations; calling a plurality of slave processors to respectively process the data of each block; and calling the master control processor to receive the processing result of each slave processor. By applying the method and the device, the finite element reverse time migration of accurate imaging can be obtained, and under the bottleneck that the original computer cluster cannot bear, the requirements of computing resources and storage resources are remarkably reduced, so that the computer cluster can perform user-acceptable imaging processing, and the method and the device are very suitable for industrial application and popularization.

Description

technical field [0001] The invention belongs to the field of seismic imaging in oil and gas exploration and development, and more specifically relates to a finite element-based reverse-time migration method and a finite-element-based reverse-time migration device. Background technique [0002] At present, the seismic prestack reverse time migration methods that have been industrialized are all based on the finite difference method of different difference schemes. The finite difference reverse time migration imaging method is simple in calculation and high in efficiency, which meets the timeliness requirements of industrial production. However, this finite-difference reverse time migration imaging method has low imaging accuracy when facing extremely irregular surface or underground rock mass. [0003] There are also a few researchers working on the finite element-based pre-stack reverse time migration method, which has strong boundary adaptability and can accurately image e...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G01V1/36
CPCG01V1/36G01V2210/512
Inventor 刘立民刘定进姚晓龙李博
Owner CHINA PETROLEUM & CHEM CORP
Features
  • R&D
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com