Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

A Method for Realizing Finite Time Control of Nonlinear Active Suspension System

An active suspension and limited time technology, applied in the field of control, can solve the problems of large amount of calculation and affect the practical application of neural network, etc., and achieve the effect of compensating time lag

Active Publication Date: 2022-08-09
GUANGDONG UNIV OF TECH
View PDF0 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0003] In the existing literature on the nonlinearity of the finite-time stability of the system and the active suspension system, most of them use neural networks or adaptive neural networks to fit the nonlinear functions of the system. The amount of calculation is large, which seriously affects the practical application of neural networks

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • A Method for Realizing Finite Time Control of Nonlinear Active Suspension System
  • A Method for Realizing Finite Time Control of Nonlinear Active Suspension System
  • A Method for Realizing Finite Time Control of Nonlinear Active Suspension System

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

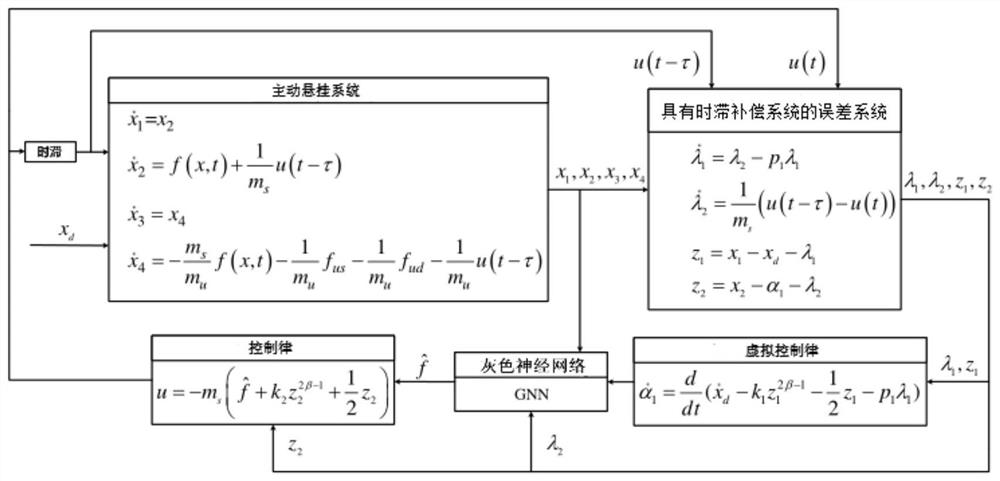
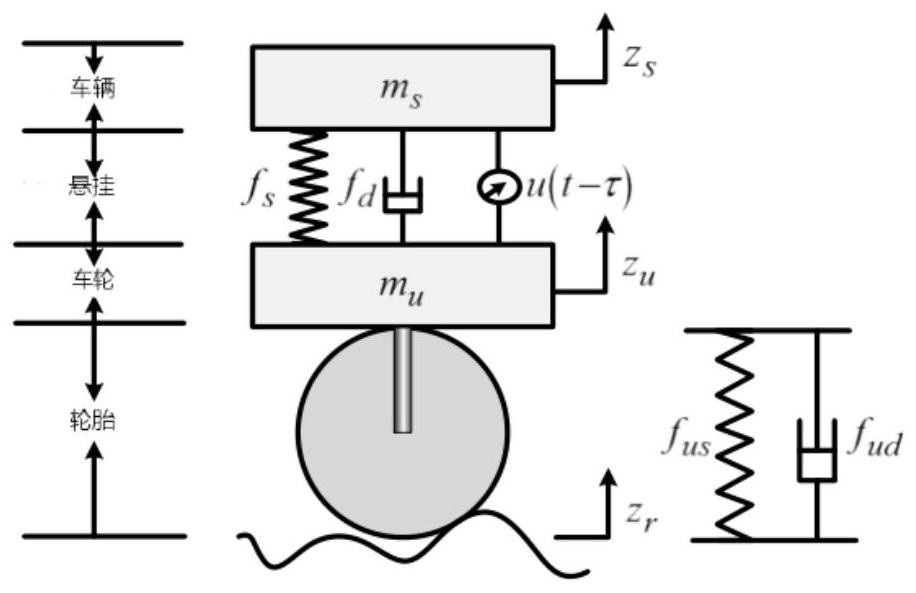
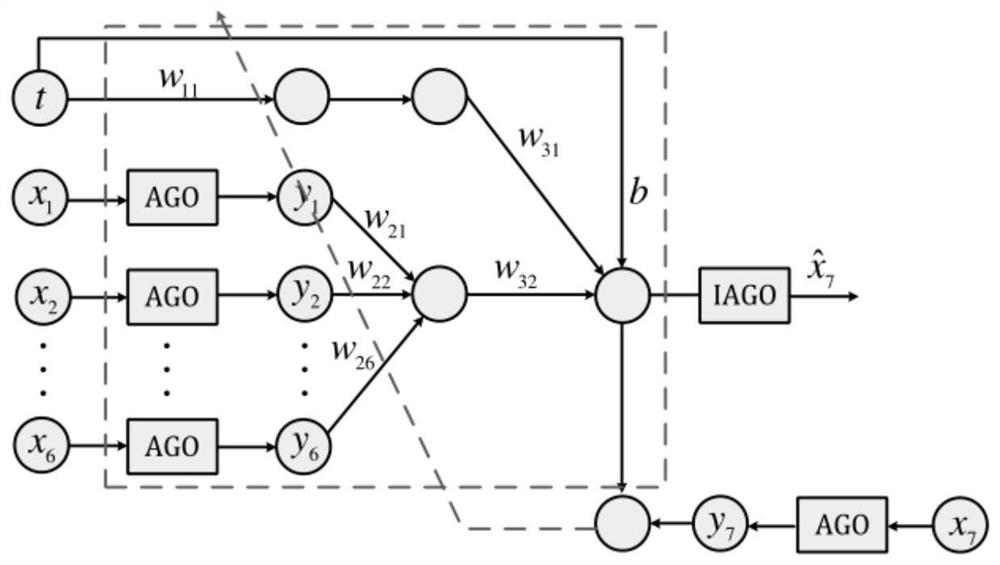
[0074] see Figure 1-Figure 3 , the method for realizing finite time control of nonlinear active suspension system of the present invention comprises the following steps:

[0075] (1) Establish the model equation of the active suspension system, analyze the space state of the active suspension system and the performance indicators that need to be improved, among which,

[0076] Performance metrics to be improved include sprung mass acceleration Suspension deflection z s -z u , tire deflection z u -z r ;

[0077] The model equation of the active suspension system is:

[0078]

[0079] where z s ,z u are the vertical displacements of the sprung and unsprung masses, respectively, z r is the input of the road, m s , m u are the sprung and unsprung masses, respectively, u is an actively controlled force generator with a constant time delay τ, f s , f d is the spring force and damping force function of the suspension component with nonlinear factors, f us , f ud T...

Embodiment 2

[0128] The following compares the passive suspension system (PSS) without a controller, the finite-time controller (FT) with a control law, and the goal controller with a controller law (GNNFT);

[0129] (1), sinusoidal road test

[0130] The parameter settings of the active suspension model can be found in the following table (Table 1);

[0131]

[0132] Set β = 19 / 20, k 1 =1, p 1 =60 / 4, k 2 =100, p 2 =6, and assumes the actuator has a constant actuator delay;

[0133] Road disturbances are:

[0134] z r =0.002sin(6πt);

[0135] The FT control law is:

[0136] u=m s (u n +u c );

[0137] where, u c is the external disturbance compensator, u n is the nominal controller satisfying:

[0138]

[0139] in,

[0140]

[0141] The GNNFT control law u is:

[0142]

[0143] When τ=30ms, it can be clearly seen that the acceleration spectrum of GNNFT (see Figure 4 ) has a peak near the resonant frequency with a maximum value, while FT has another peak at ot...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a method for realizing finite-time control of a nonlinear active suspension system. First, a model equation of the active suspension system is established to analyze the space state of the active suspension system and performance indexes that need to be improved; and then an error system with time delay compensation is established. , the influence of the time delay of the active suspension system is compensated by the auxiliary system; secondly, the Lyapunov function relationship is established through the error system, and the virtual control law a is obtained by using the inversion technique 1 , the control law u, to improve the corresponding performance indicators; the approximate nonlinear function of the compensated error system is obtained through the gray neural network training again; finally, after the correction of the control law u, a new and smaller time delay effect of the active suspension system is generated, The method of the present invention is repeatedly and continuously cycled in a limited time, thereby realizing stable control of the active suspension system in a limited time.

Description

technical field [0001] The invention relates to a control method, in particular to a method for realizing finite time control of a nonlinear active suspension system. Background technique [0002] For the control of active suspension systems, most of the existing controls are based on progressive stability. The disadvantage of asymptotic stability is that the time when the system reaches the stable state cannot be determined, and the time to reach the stable state is related to the rapidity of the system, so the control based on asymptotic stability is difficult to achieve the rapidity of the system. The control based on finite time stability can make the system reach a stable state within a specified time, so it is more likely to realize the rapidity of the system. [0003] In the existing literatures on the finite-time stability of the system and the nonlinearity of the active suspension system, most of them use the neural network or the adaptive neural network to fit the...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G05B13/04
CPCG05B13/042Y02T90/00
Inventor 黄运保梁桂铭林志跃詹宏远周健松
Owner GUANGDONG UNIV OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com