Rapid searching method for entropy layer characteristic value
A technology of eigenvalues and interpolation methods, which is applied in the field of fast search for entropy layer eigenvalues, can solve problems such as difficult to find eigenvalue solutions, increase the amount of calculation, and inability to judge entropy layer eigenvalue solutions, etc., to achieve fast calculation and search speed, The effect of reducing time cost and facilitating the stability analysis of entropy layer
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment 1
[0039] Embodiment 1: a kind of quick search method of entropy layer characteristic value, comprises steps:
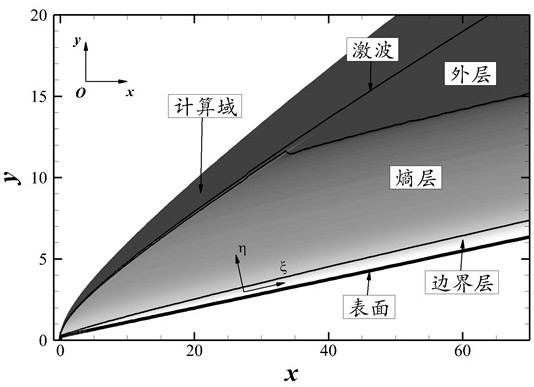
[0040] S1, to obtain the laminar flow field;
[0041] S2, extract the laminar flow calculation section: transform the laminar flow field obtained in step S1 into the body-fitted coordinate system through coordinate transformation, and then use the interpolation method to interpolate the flow field to the orthogonal grid to obtain the flow field on the vertical surface Calculate the profile;
[0042] S3, find the entropy layer eigenvalue: given the initial eigenvalue to iteratively solve;
[0043] S4, physical understanding of identifying entropy layer stability: judging whether the following conditions are met: the growth rate in the preset condition is greater than 0, and the phase velocity is in the set interval; and it must be satisfied that the eigenvalues in the frequency interval do not exist in isolation. The characteristic solution can be found near the eigenv...
Embodiment 2
[0045] Embodiment 2: On the basis of Embodiment 1, in step S1, the acquisition of the laminar flow field includes a sub-step: using a CFD computing system to calculate and obtain laminar flow field data, and the laminar flow field data includes a two-dimensional blunt cone shape.
Embodiment 3
[0046] Embodiment 3: On the basis of Embodiment 1, in step S3, the given initial eigenvalue includes sub-steps: the dimensionless frequency range of the entropy layer eigensolution is limited to the interval [0, 0.3], and the phase velocity It is limited to the interval [0.8, 0.9], and the interval between the phase velocities is 0.01, and the growth rate is limited to the order of 0.0001.
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com