Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Spaceflight measurement and control resource scheduling efficiency evaluation method based on graduatory fuzzy set

A technology for aerospace measurement and control and resource scheduling, applied in the field of aerospace scheduling efficiency, can solve problems such as discrepancies in evaluation results, inability to express hesitant states, and constraints on expressing and processing uncertain information, achieving reasonable and accurate evaluation, good engineering applicability, and application scope. expansive effect

Pending Publication Date: 2022-04-22
CHINA XIAN SATELLITE CONTROL CENT
View PDF0 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0004] At present, the commonly used fuzzy comprehensive evaluation method has two limitations: on the one hand, fuzzy sets can only express two states of support and opposition, and cannot express the state of hesitation between support and opposition, and are restricted in expressing and processing uncertain information. On the other hand, the fuzzy comprehensive evaluation method only uses the membership degree information, resulting in a large discrepancy between the evaluation results and the actual situation

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Spaceflight measurement and control resource scheduling efficiency evaluation method based on graduatory fuzzy set
  • Spaceflight measurement and control resource scheduling efficiency evaluation method based on graduatory fuzzy set
  • Spaceflight measurement and control resource scheduling efficiency evaluation method based on graduatory fuzzy set

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0095] This embodiment provides a Pythagorean fuzzy set theory-based method for evaluating the efficiency of spaceflight measurement and control resource scheduling, the method comprising:

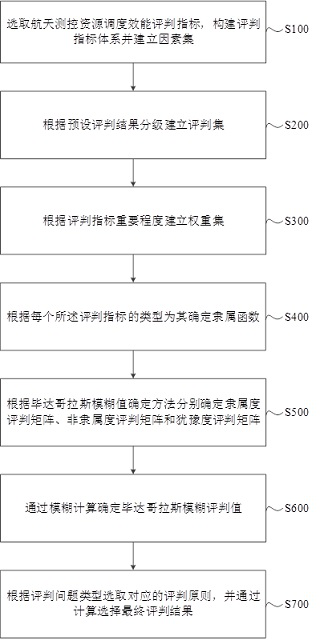
[0096] S01, select the evaluation index of spaceflight measurement and control resource dispatching efficiency, construct the evaluation index system, and establish the factor set;

[0097] S02, grading according to the preset judgment results, and establishing a judgment set;

[0098] S03, establishing a weight set according to the importance of the evaluation index;

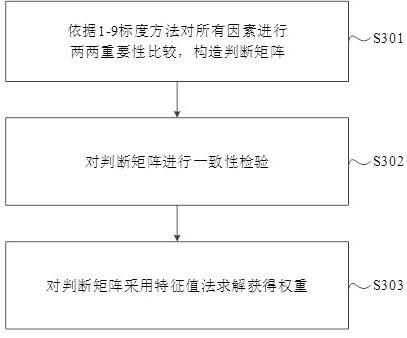
[0099] Table 2 lists the judgment matrix G given by the 1-9 scaling method, and the consistency test is performed on it to obtain CR=0.0246<0.1, that is, the consistency level of the judgment matrix G meets the requirements, and the eigenvalue method is used for it Solve to get the weight set as:

[0100] W = {0.1717, 0.0355, 0.0624, 0.4189, 0.1048, 0.0450, 0.0612, 0.1005}.

[0101] Table 2 Judgment matrix

[0102]

...

Embodiment 2

[0126] The main difference between this embodiment and the preferred embodiment one is that the evaluation question type is multi-object evaluation.

[0127] The implementation steps of S01-S04 are completely the same as those of the first preferred embodiment above.

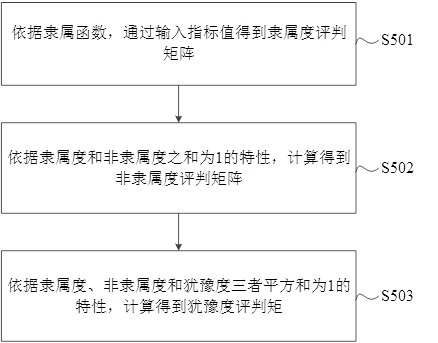
[0128] S05, according to the Pythagorean fuzzy value determination method, respectively determine the membership evaluation matrix, the non-membership evaluation matrix and the hesitation evaluation matrix;

[0129] Table 7 lists the index values ​​of the three input evaluation objects, and the three evaluation objects are denoted as A 1 , A 2 , A 3 . According to the determination method of Pythagorean fuzzy evaluation value, the membership evaluation matrix, non-membership evaluation matrix and hesitation evaluation matrix of the three evaluation objects are calculated and determined respectively, as follows:

[0130]

[0131]

[0132]

[0133]

[0134] Table 7 Index values ​​of the three evalu...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to a spaceflight measurement and control resource scheduling efficiency evaluation method based on a graduatory fuzzy set, and the method comprises the steps: selecting spaceflight measurement and control resource scheduling efficiency evaluation indexes, constructing an evaluation index system, and building a factor set; grading and establishing an evaluation set according to a preset evaluation result; establishing a weight set according to the importance degree of the evaluation indexes; determining a membership function according to the evaluation index type; determining a membership degree evaluation matrix, a non-membership degree evaluation matrix and a hesitation degree evaluation matrix according to the graduatory fuzzy value; determining a graduatory fuzzy evaluation value through fuzzy calculation; and selecting a corresponding judgment principle according to the judgment problem type, and selecting a final judgment result through calculation. According to the method, the influence of uncertainty on the aerospace measurement and control resource scheduling efficiency judgment result is effectively overcome, uncertain information is utilized, subjective preference of people is reserved, the aerospace measurement and control resource scheduling efficiency can be reasonably and accurately judged, the calculation process is simple, the application range is wide, and the engineering applicability is good.

Description

technical field [0001] Embodiments of the present disclosure relate to the technical field of aerospace scheduling efficiency, and in particular to a method for evaluating the scheduling efficiency of aerospace measurement and control resources based on Pythagorean fuzzy sets. Background technique [0002] Aerospace measurement and control resources are mainly responsible for spacecraft tracking and measurement, telemetry and remote control tasks, ensuring that spacecraft can complete corresponding missions while operating safely and stably. With the rapid growth of the number of spacecraft, the corresponding resource types become more diverse, the resource requirements become more diverse, and the supporting tasks become more complex. This requires a more scientific and efficient scheduling of management and control resources, and how to reasonably judge the effectiveness of current aerospace measurement and control resource scheduling is the premise and basis for scientifi...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06Q10/06G06N7/02
CPCG06Q10/06393G06Q10/0631G06N7/02
Inventor 张强刘建平王建平白剑高惠荔杨帆姚智海韩冰肖勇梁军赵若言
Owner CHINA XIAN SATELLITE CONTROL CENT
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com