Compound galois field engine and galois field divider and square root engine and method
a technology of galois field and engine, applied in the direction of instruments, computation using denominational number representation, computation using non-denominational number representation, etc., to achieve the effect of less power, less area, and easy reconfiguration
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Benefits of technology
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
[0046] Aside from the preferred embodiment or embodiments disclosed below, this invention is capable of other embodiments and of being practiced or being carried out in various ways. Thus, it is to be understood that the invention is not limited in its application to the details of construction and the arrangements of components set forth in the following description or illustrated in the drawings.
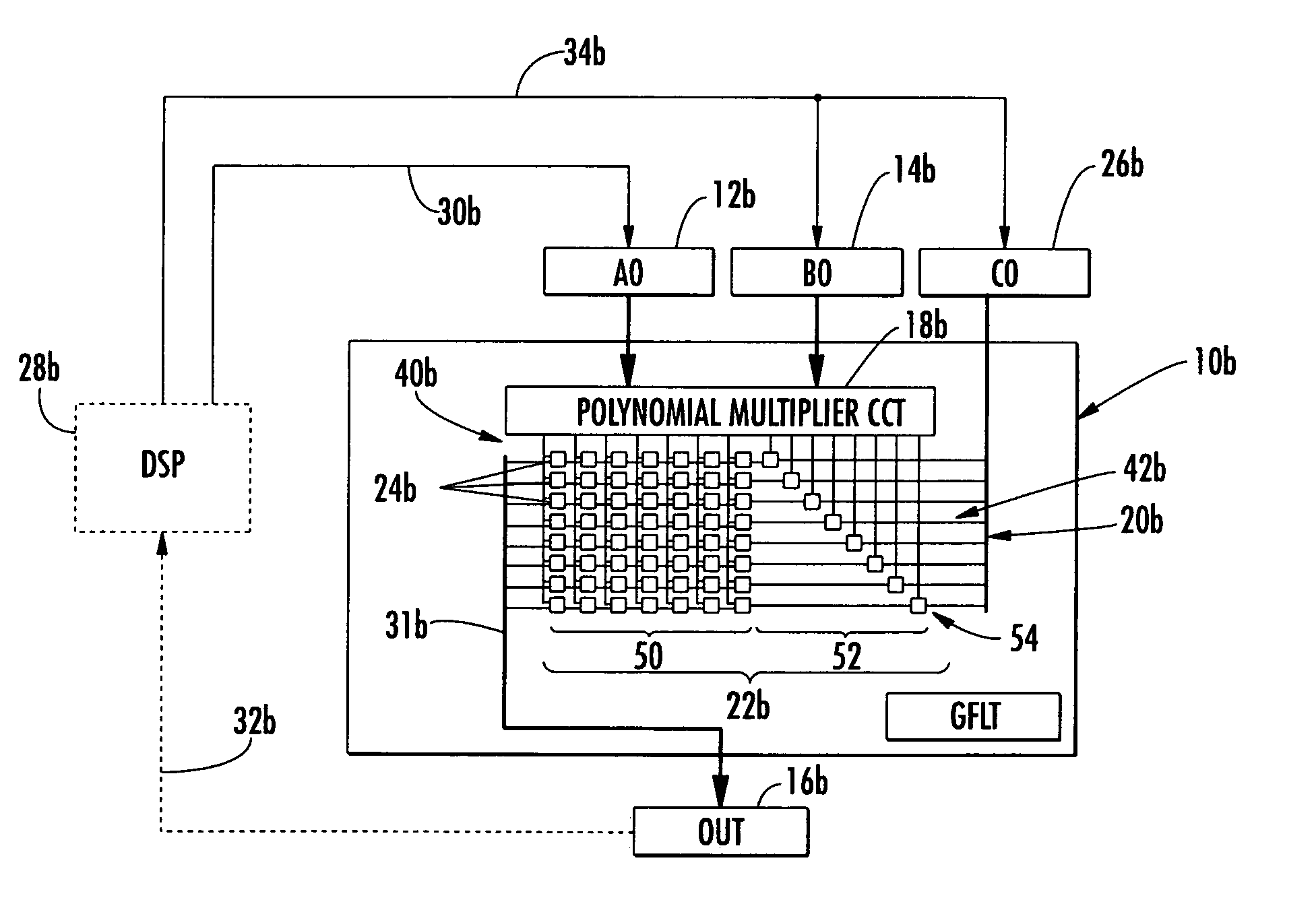
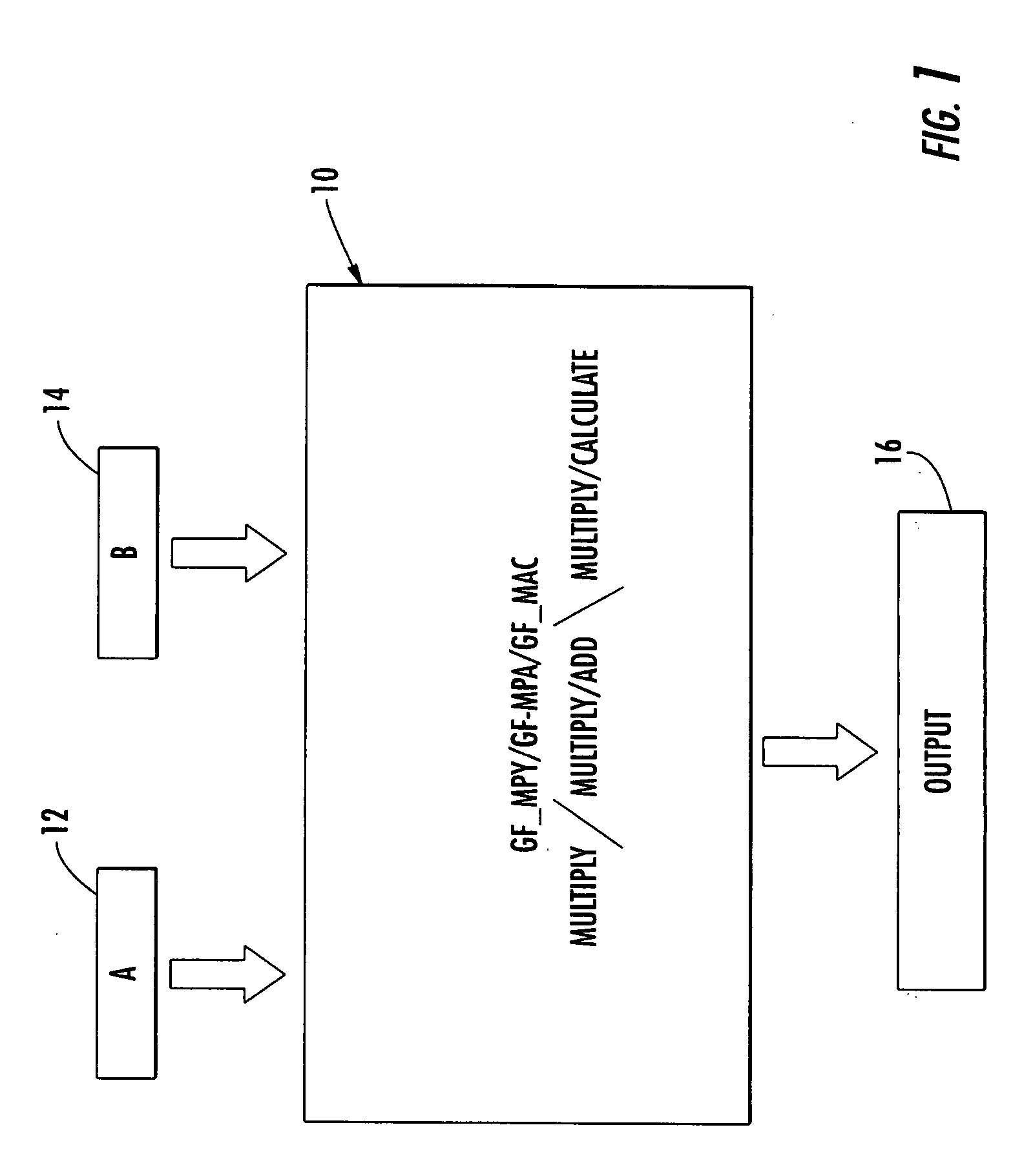
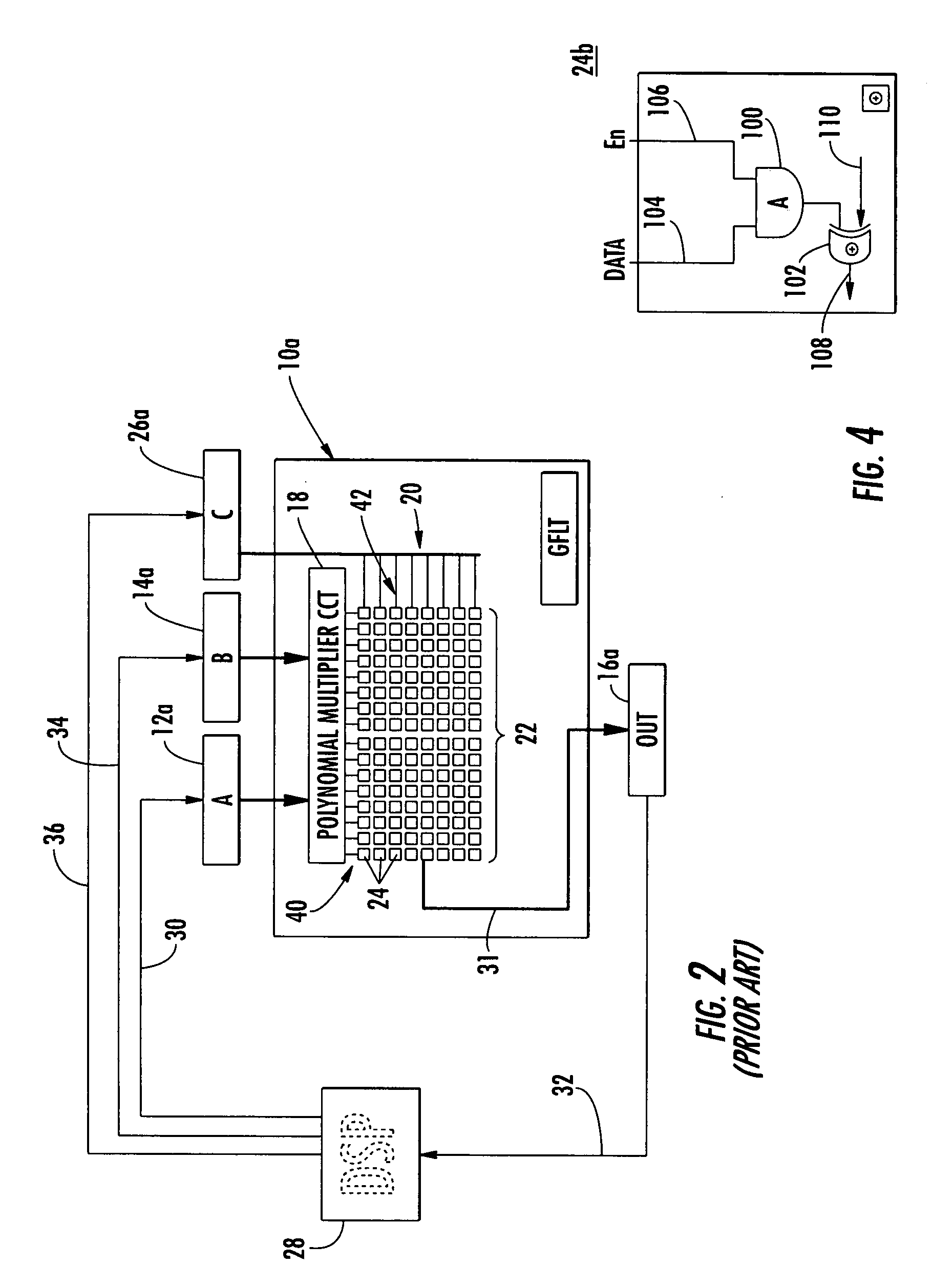
[0047] Before disclosing the compound Galois field engine and the divisor engine and method of this invention an explanation of Galois field transformers and multipliers is presented for a better understanding.
[0048] A Galois field GF(n) is a set of elements on which two binary operations can be performed. Addition and multiplication must satisfy the commutative, associative and distributive laws. A field with a finite number of elements is a finite field. An example of a binary field is the set {0, 1} under modulo 2 addition and modulo 2 multiplication and is denoted GF(2). The modulo 2...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com