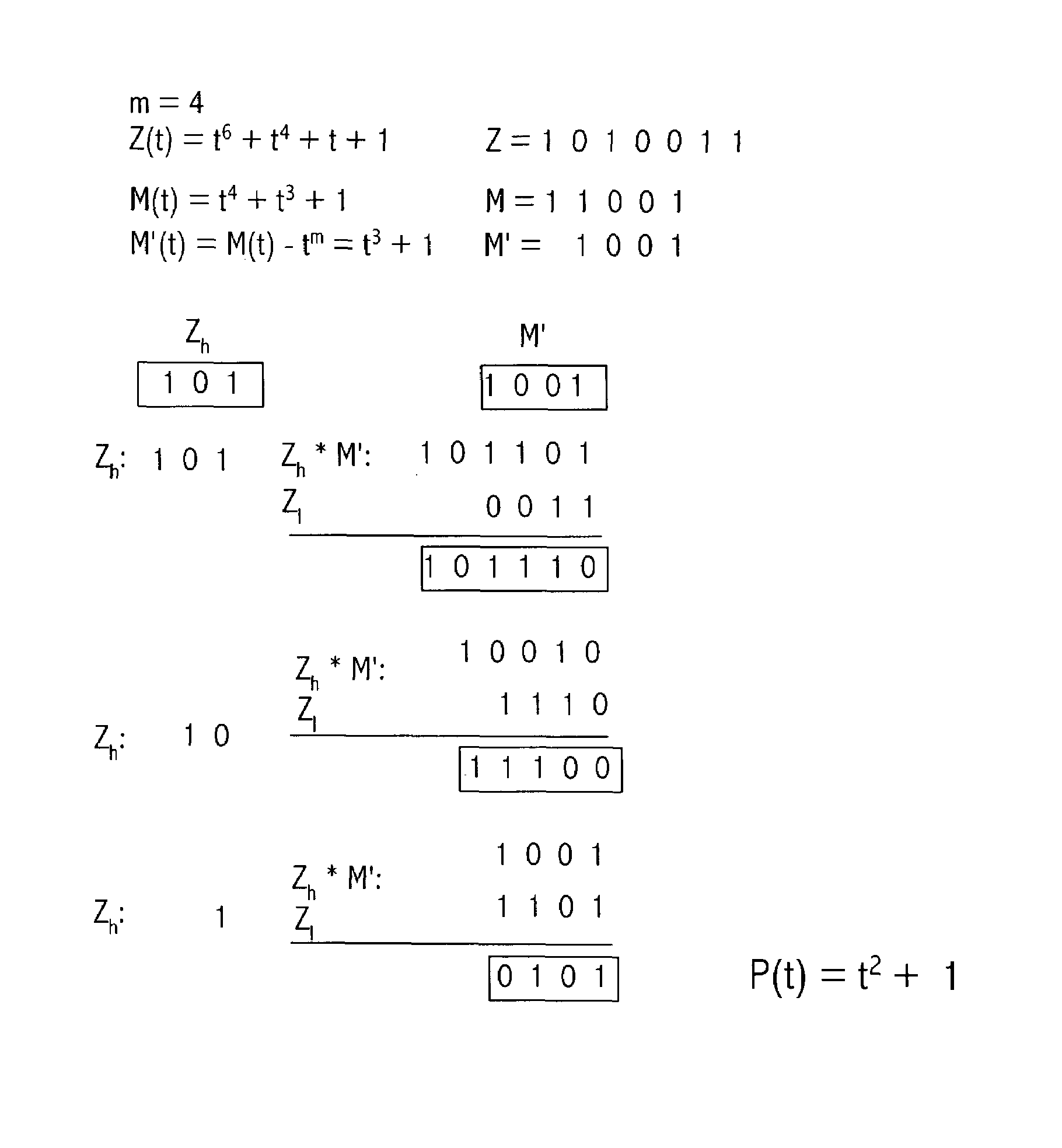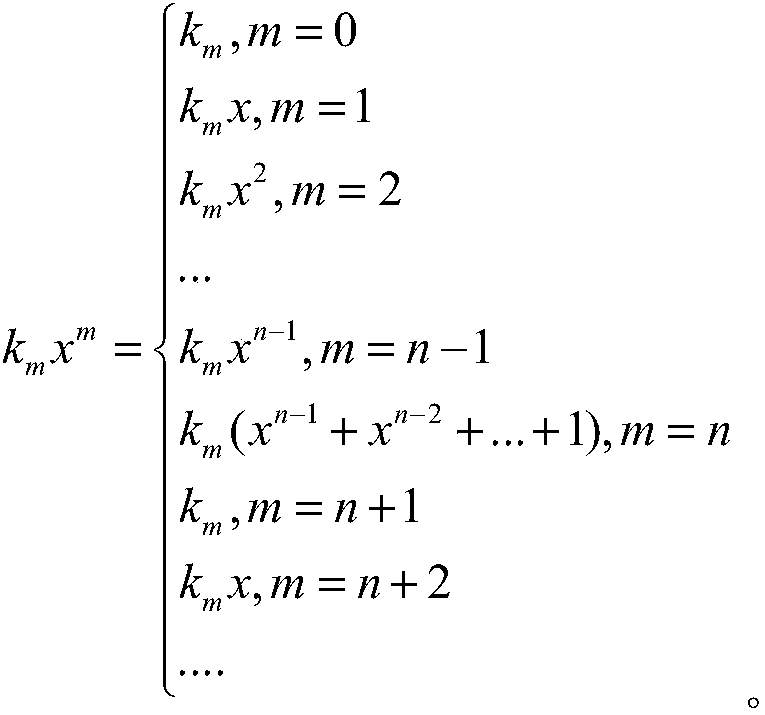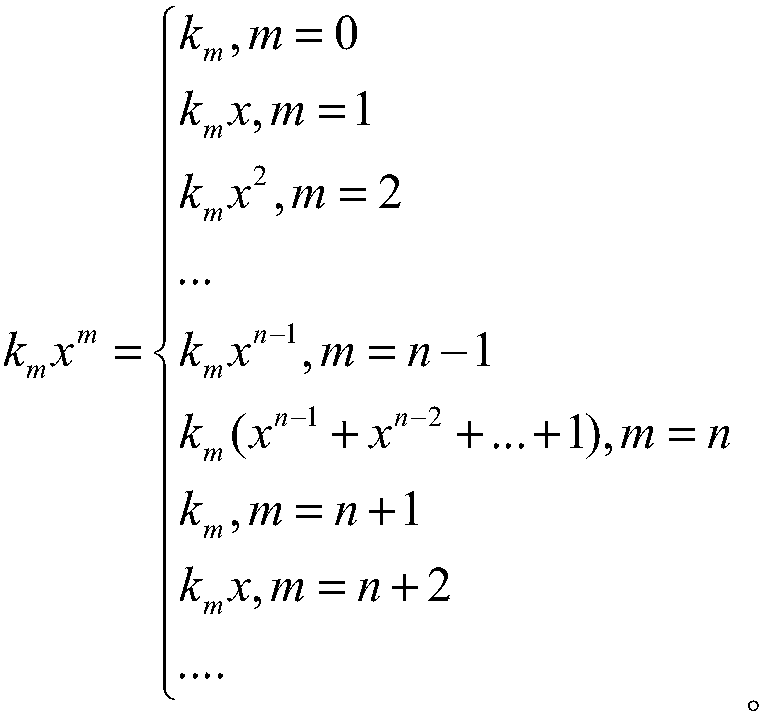Patents
Literature
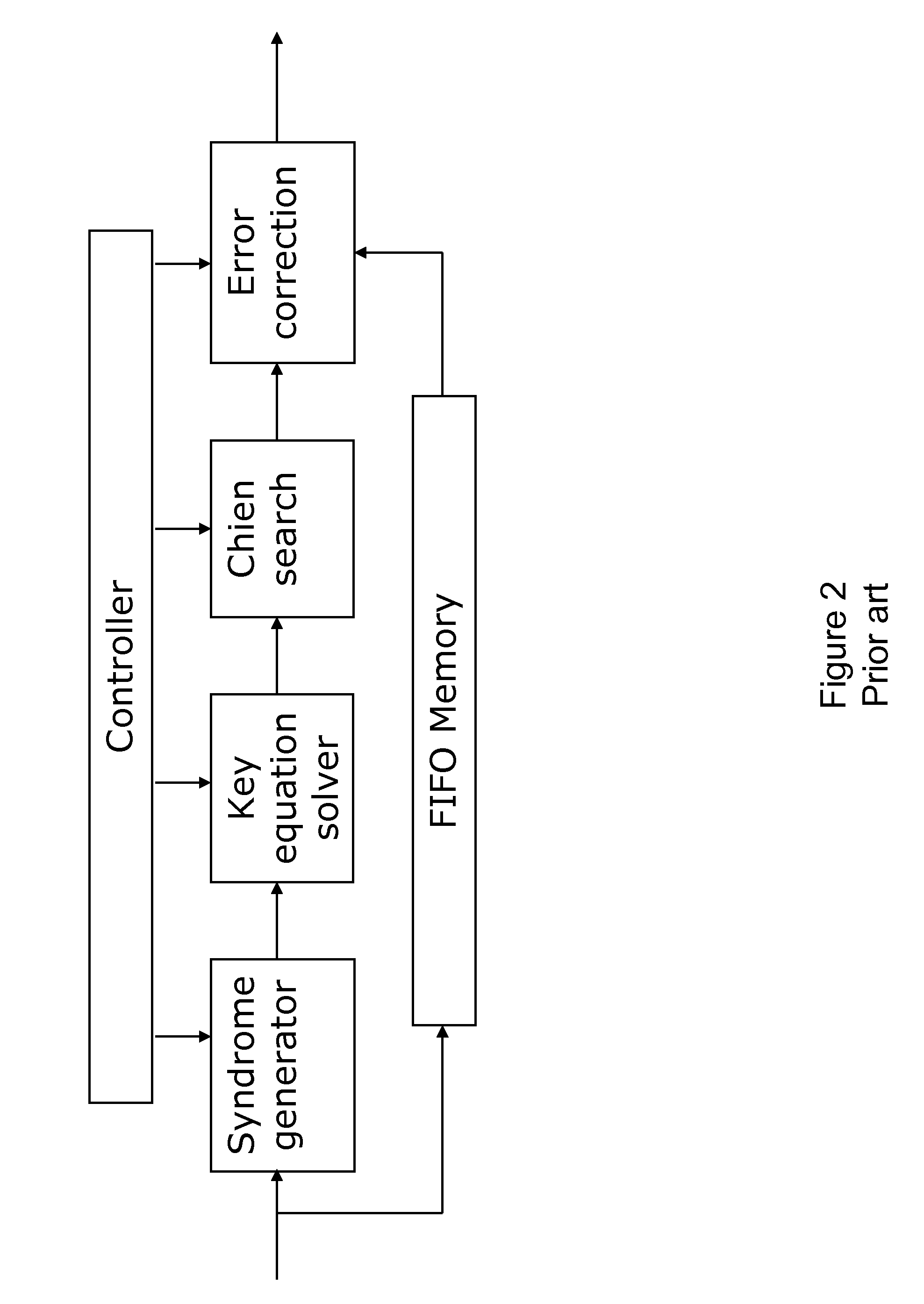
70 results about "Irreducible polynomial" patented technology
Efficacy Topic
Property
Owner
Technical Advancement
Application Domain
Technology Topic
Technology Field Word
Patent Country/Region
Patent Type
Patent Status
Application Year
Inventor
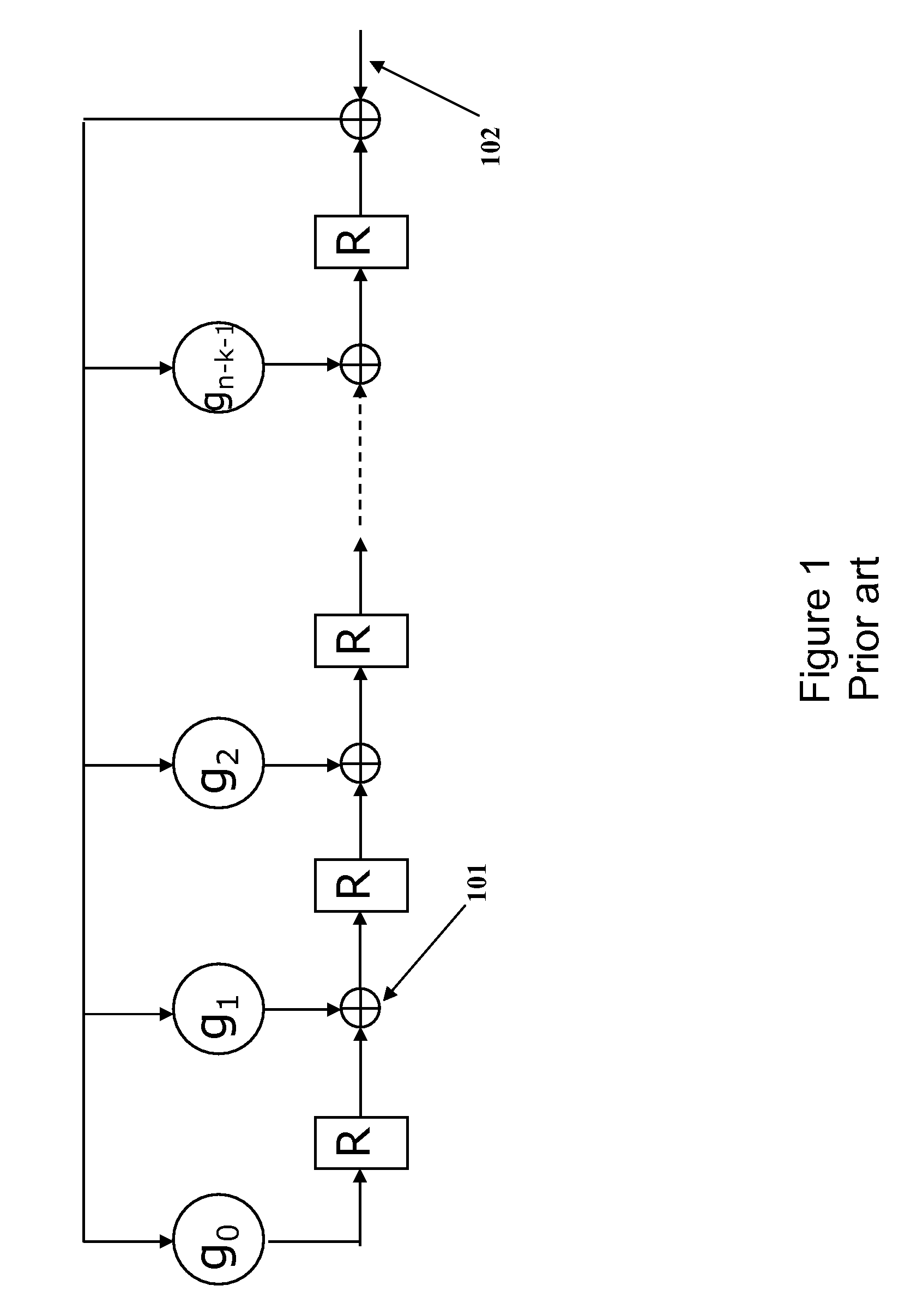
In mathematics, an irreducible polynomial (or prime polynomial) is, roughly speaking, a non-constant polynomial that cannot be factored into the product of two non-constant polynomials. The property of irreducibility depends on the nature of the coefficients that are accepted for the possible factors, that is, the field or ring to which the coefficients of the polynomial and its possible factors are supposed to belong.
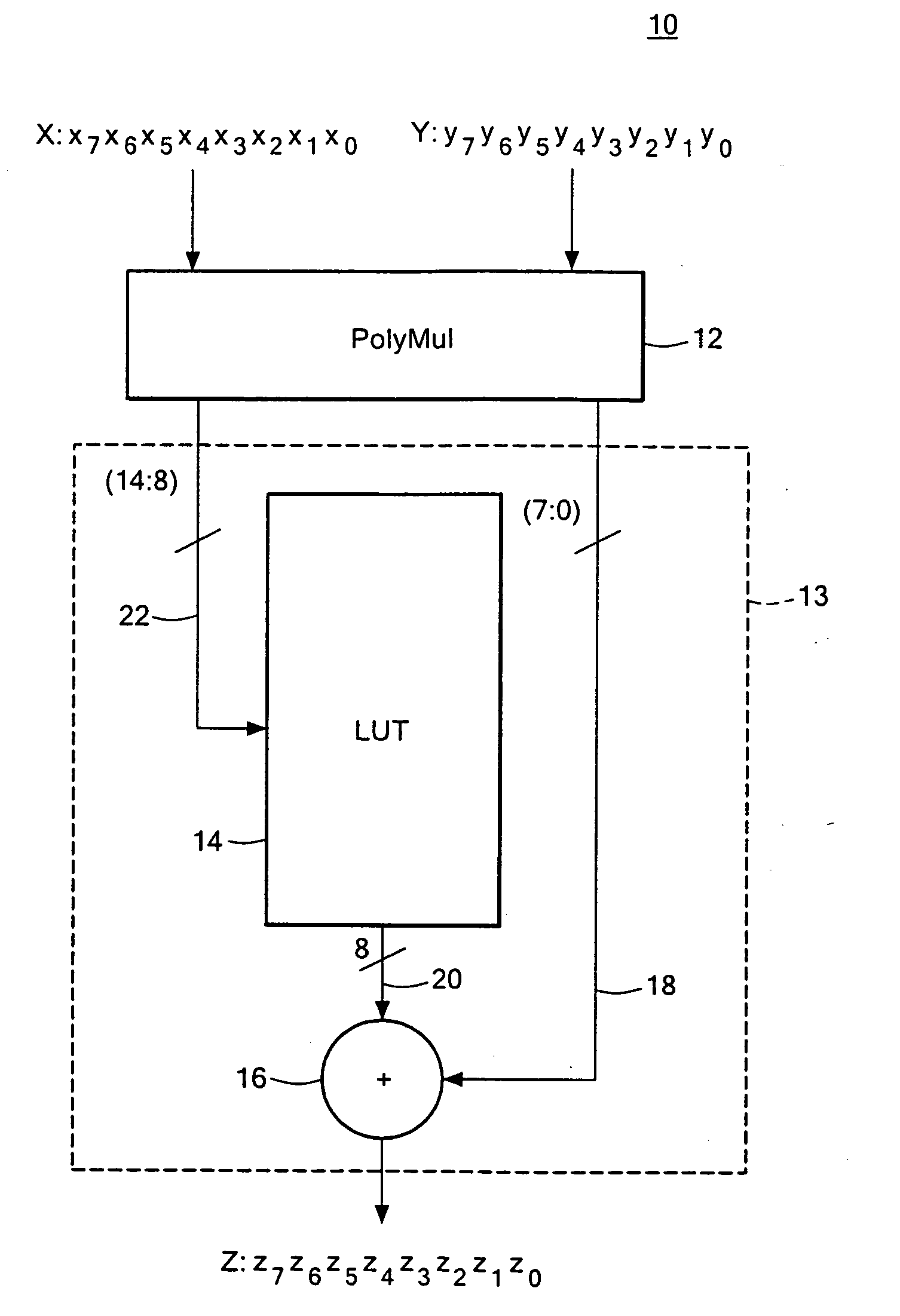
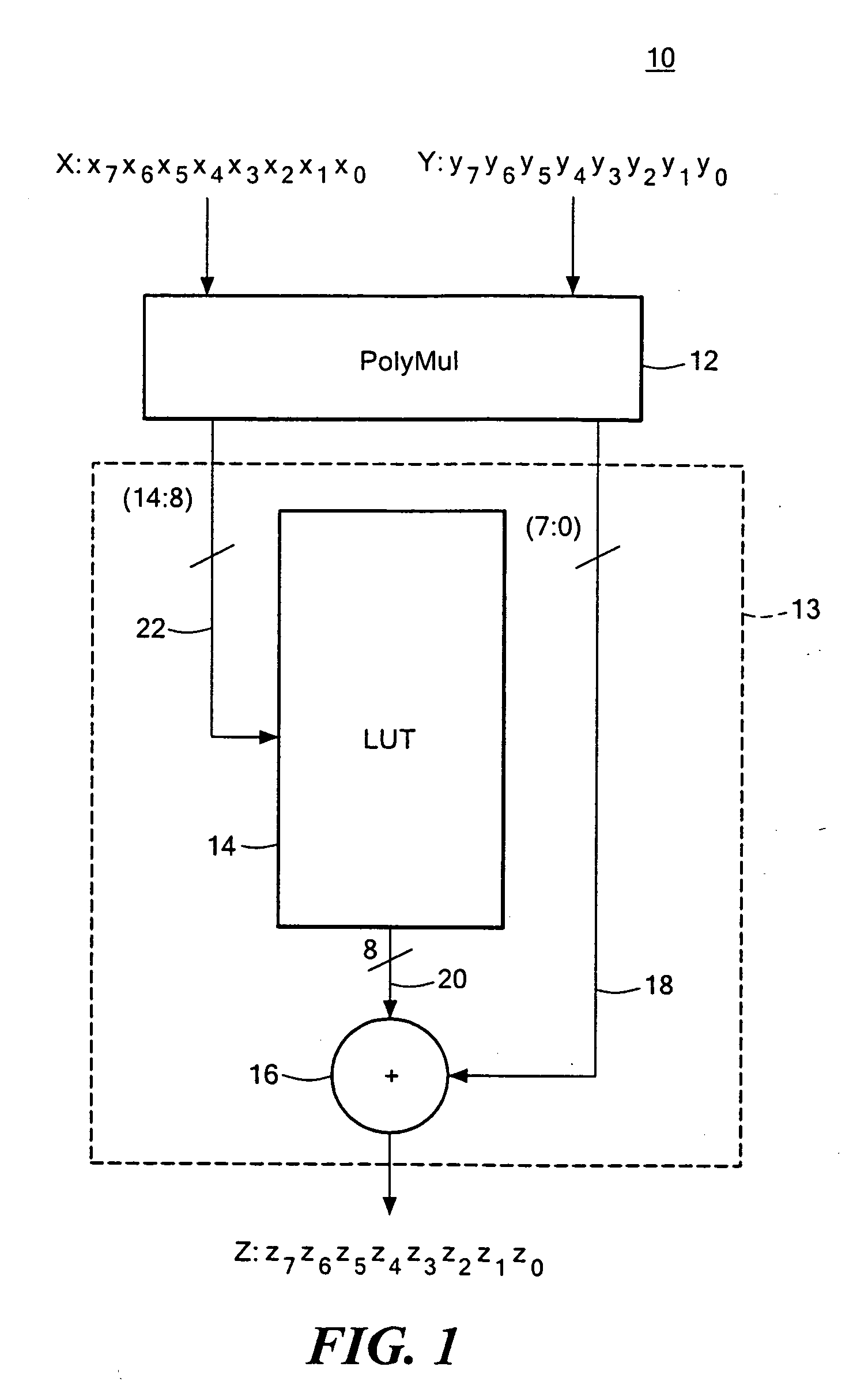
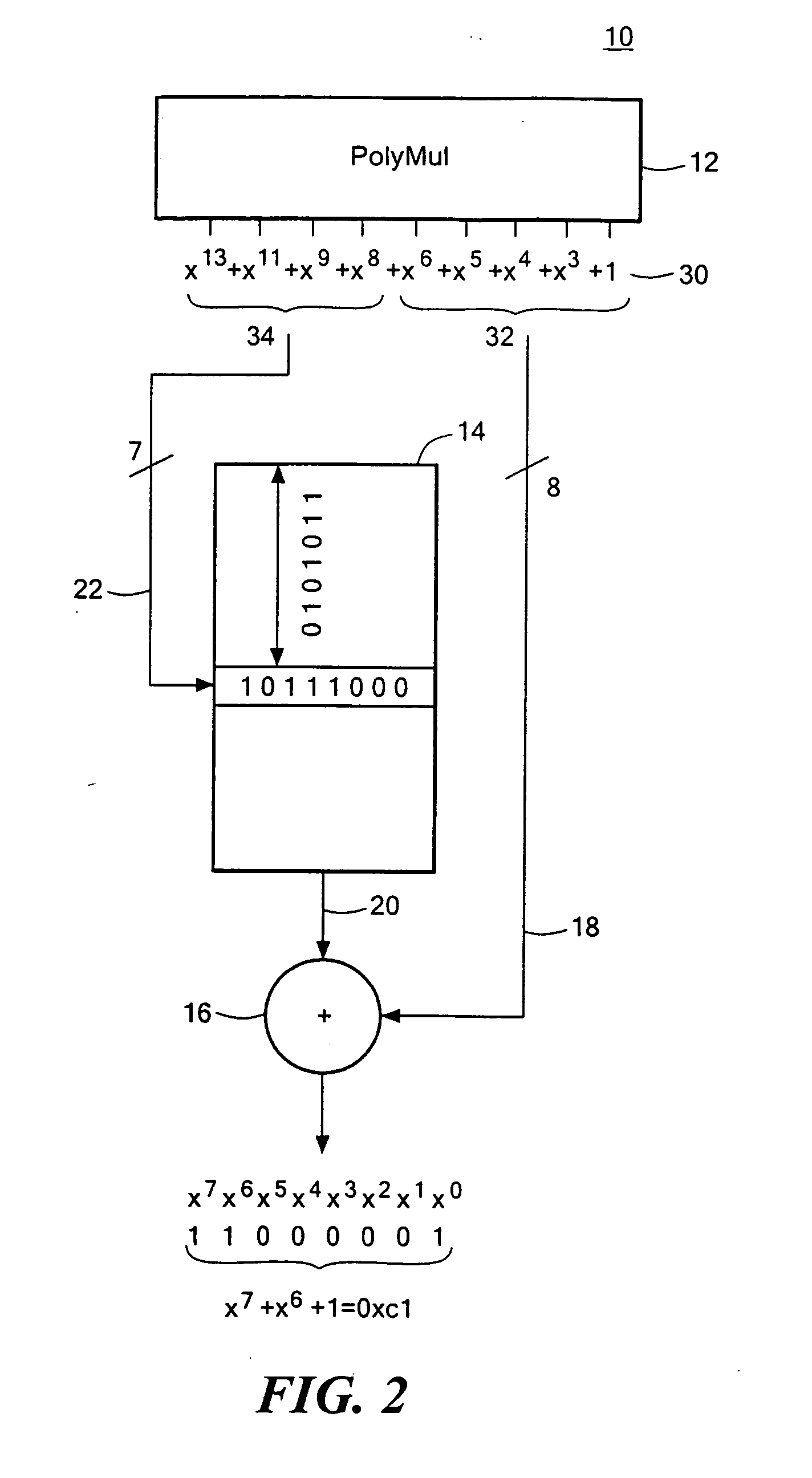
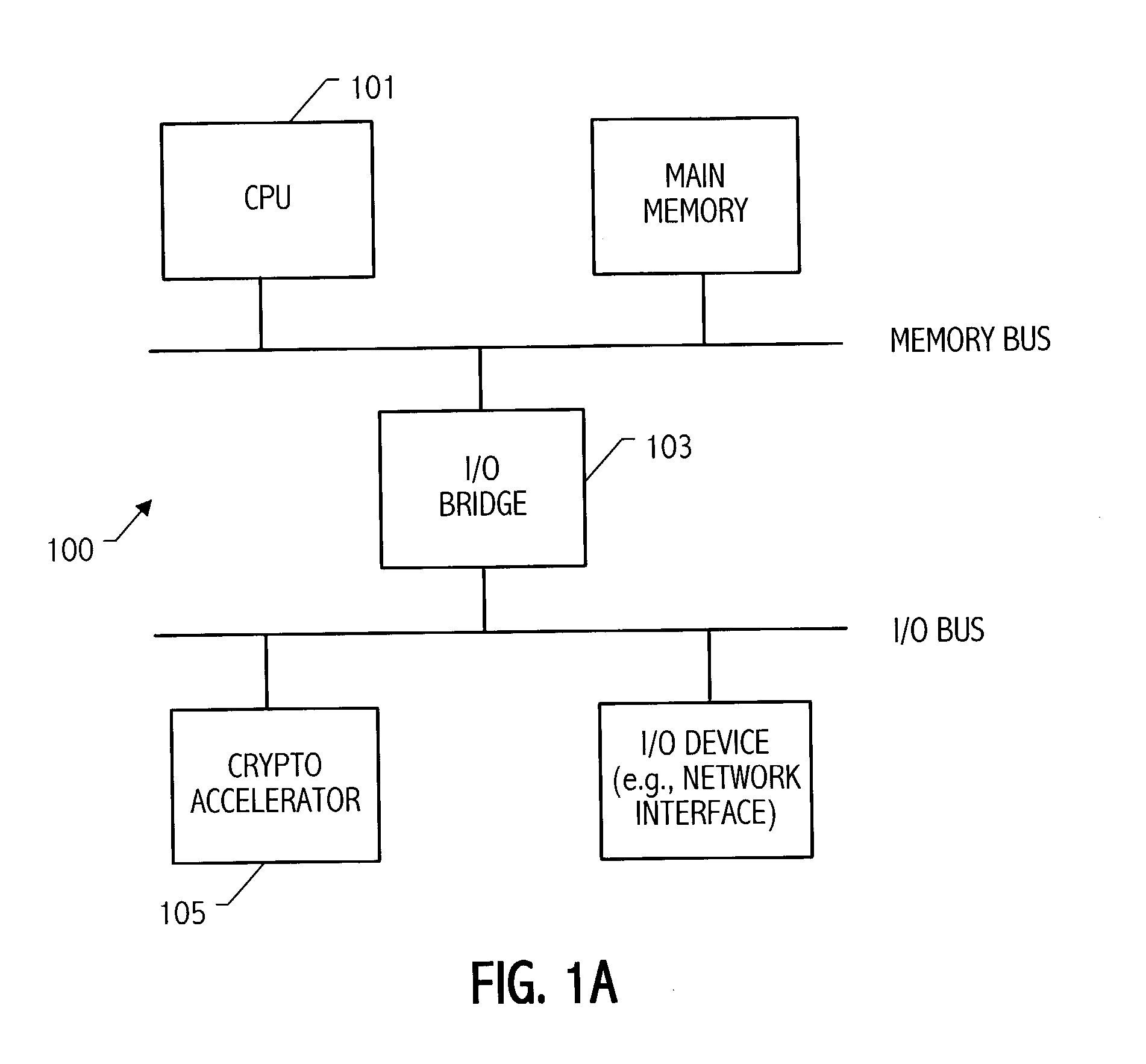
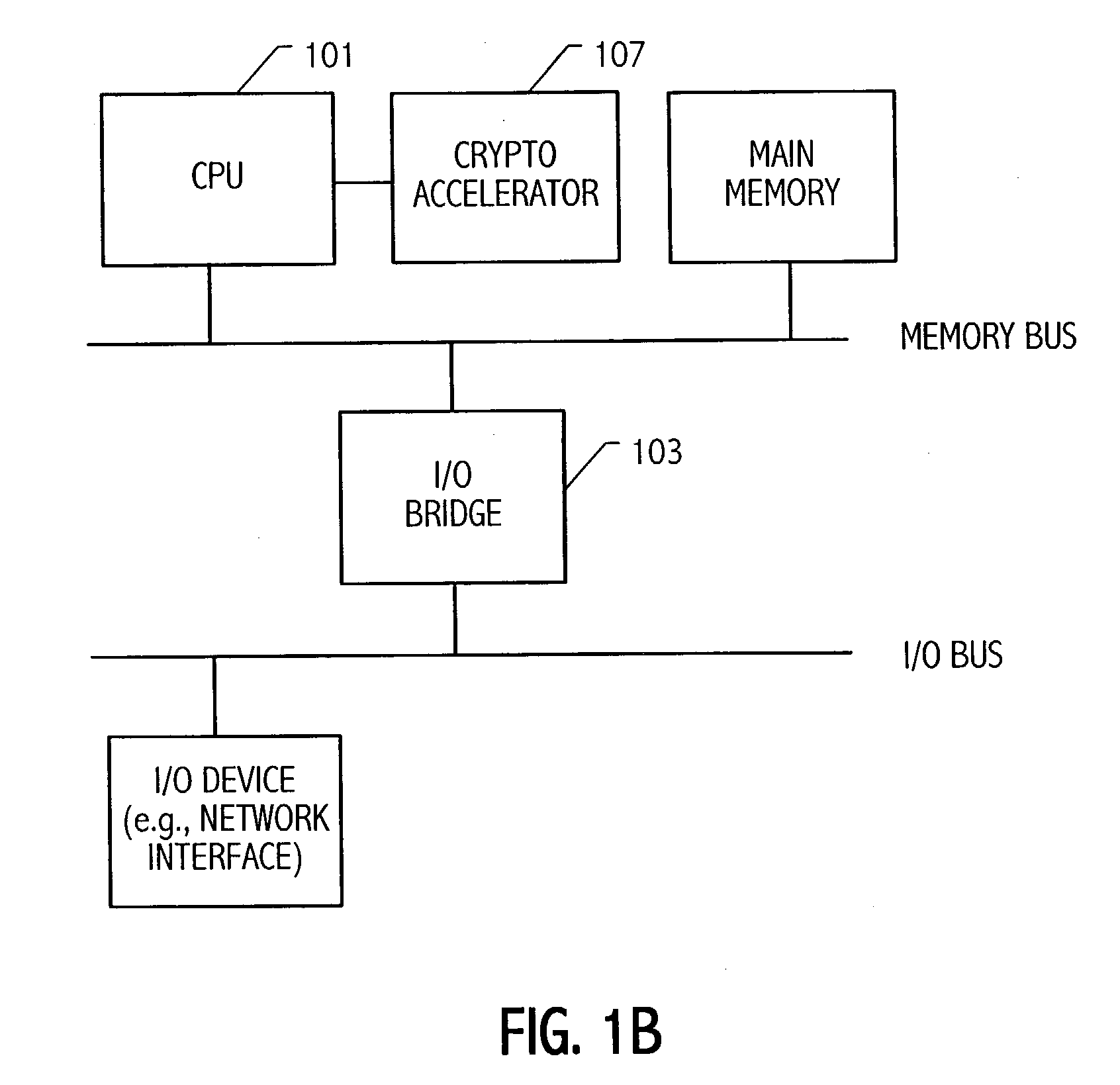
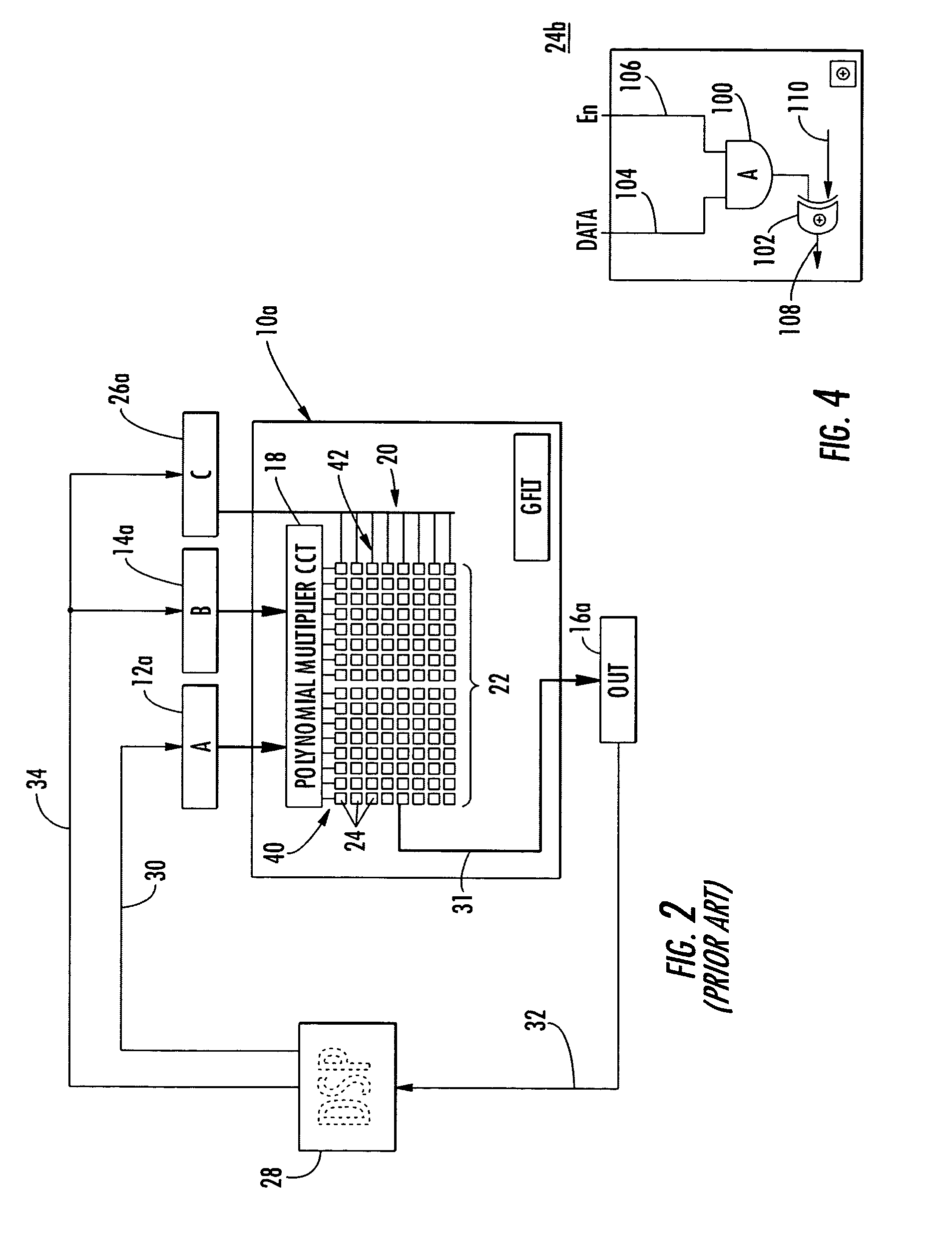
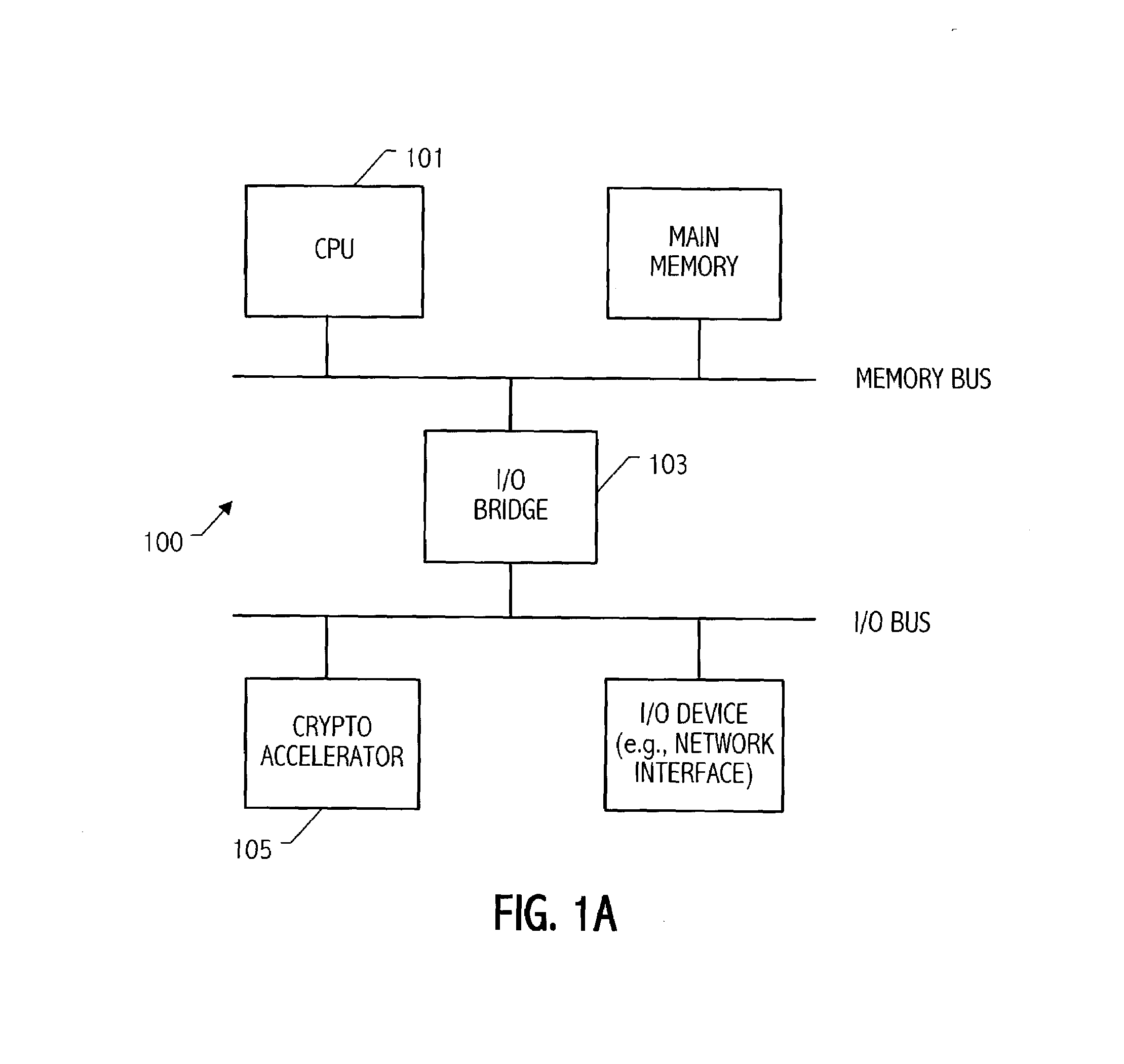
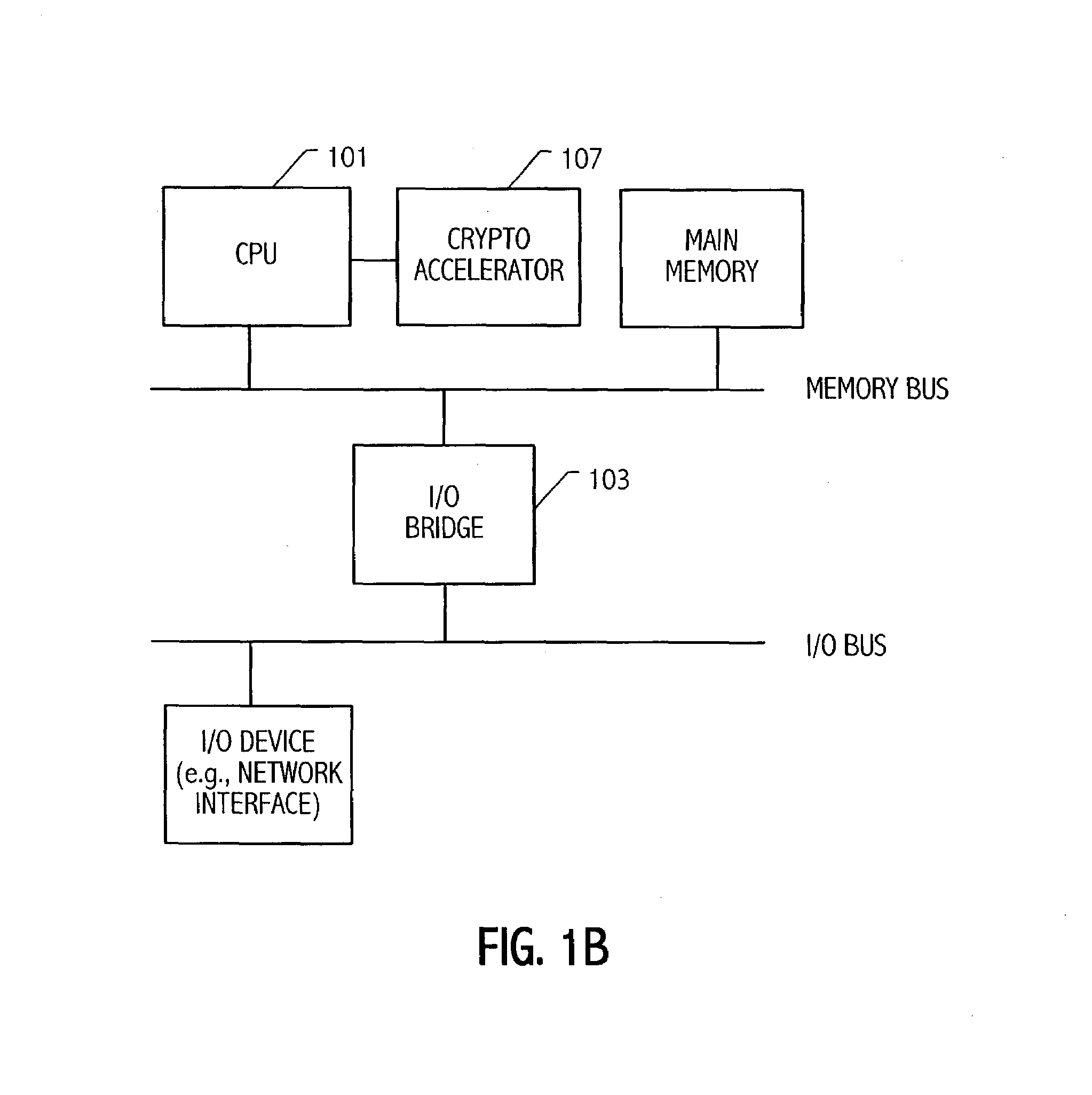
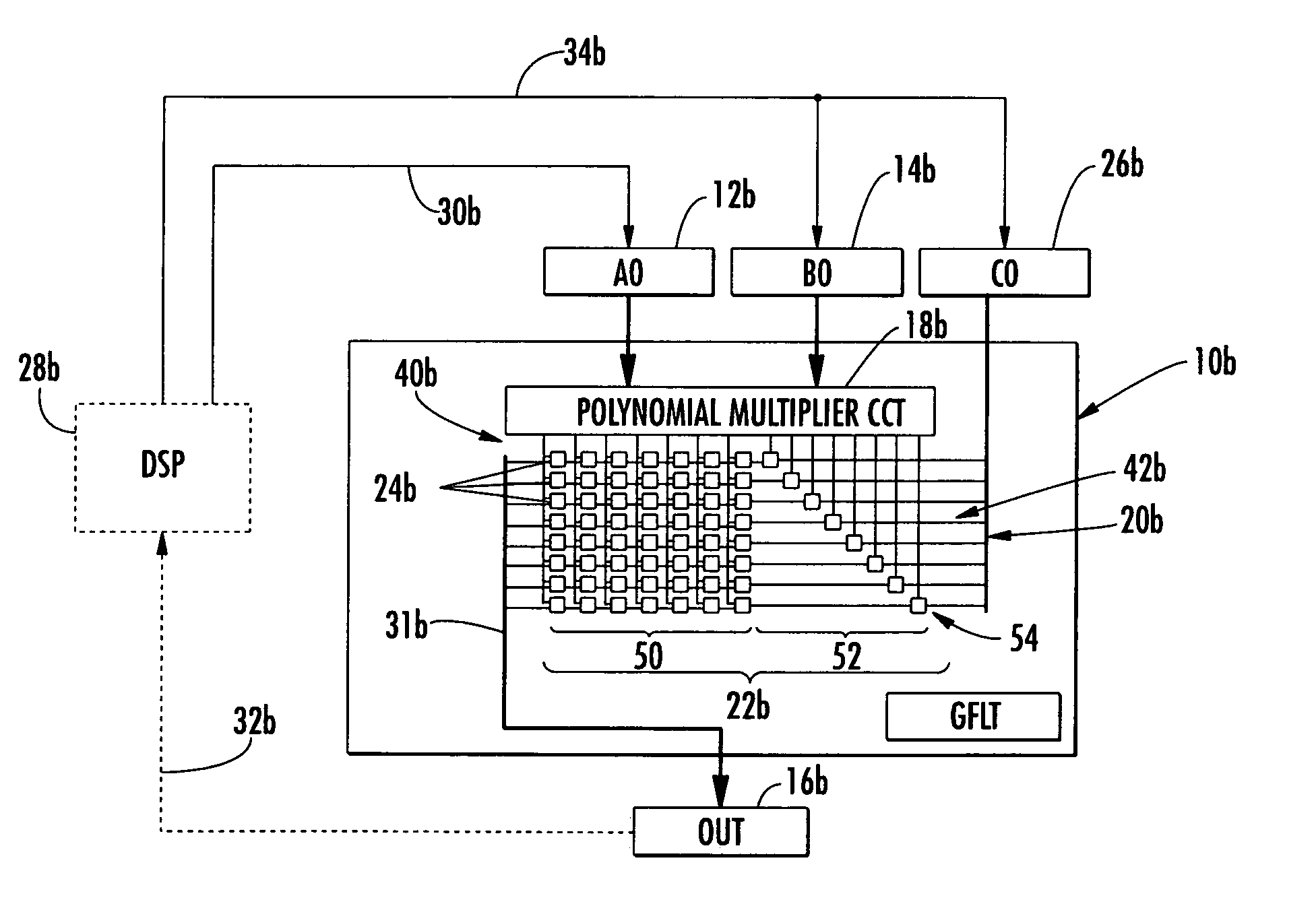
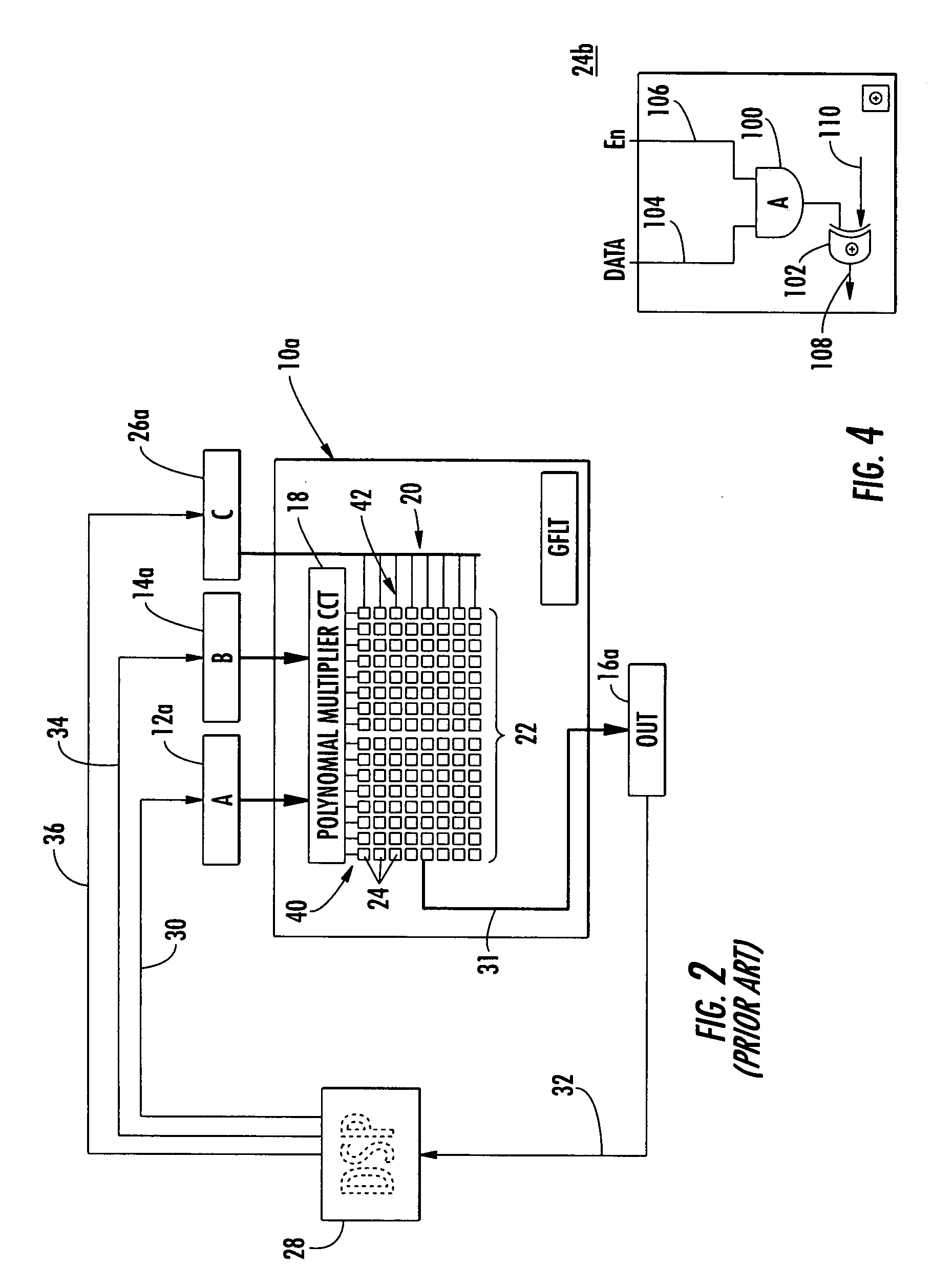
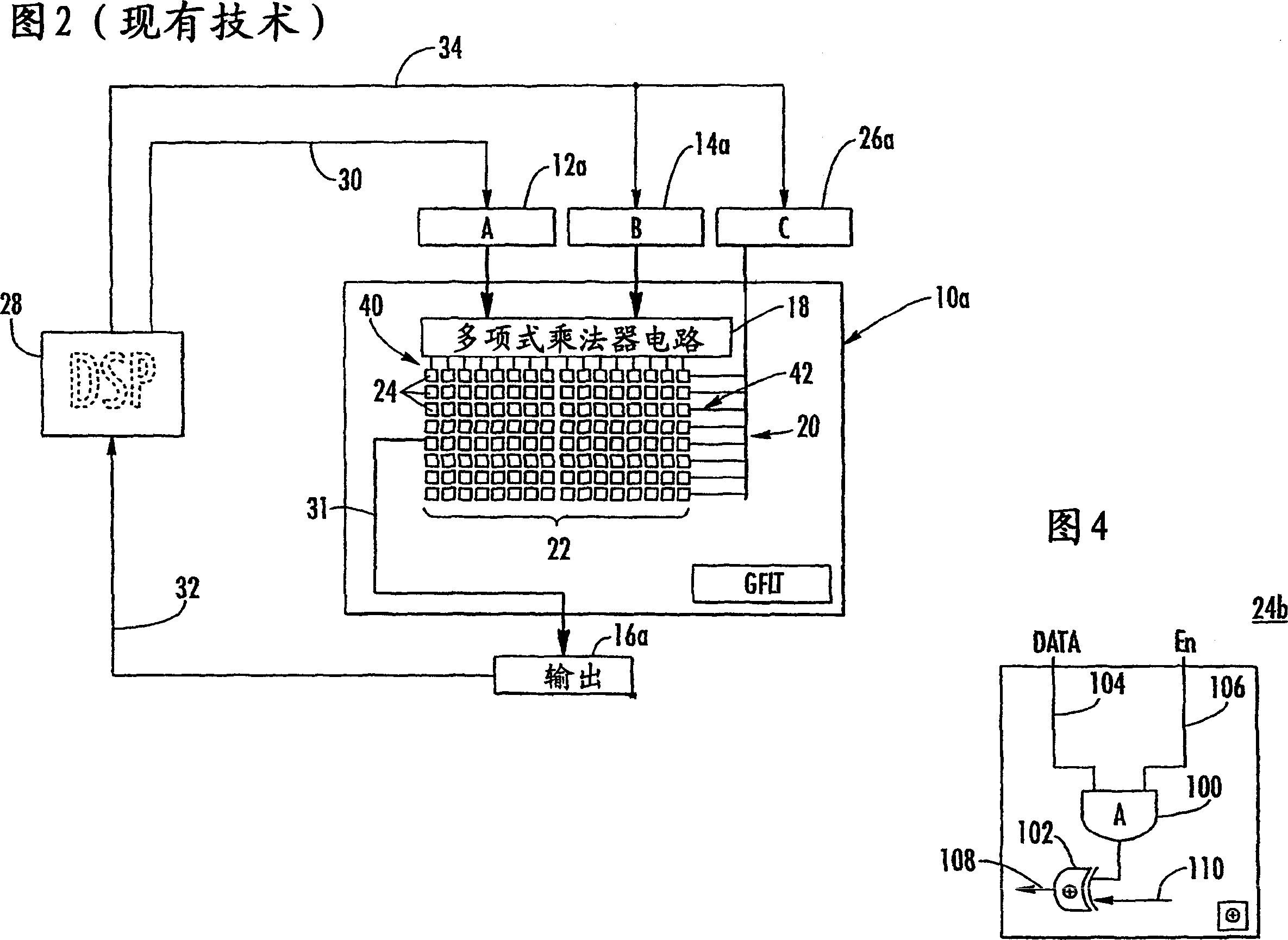
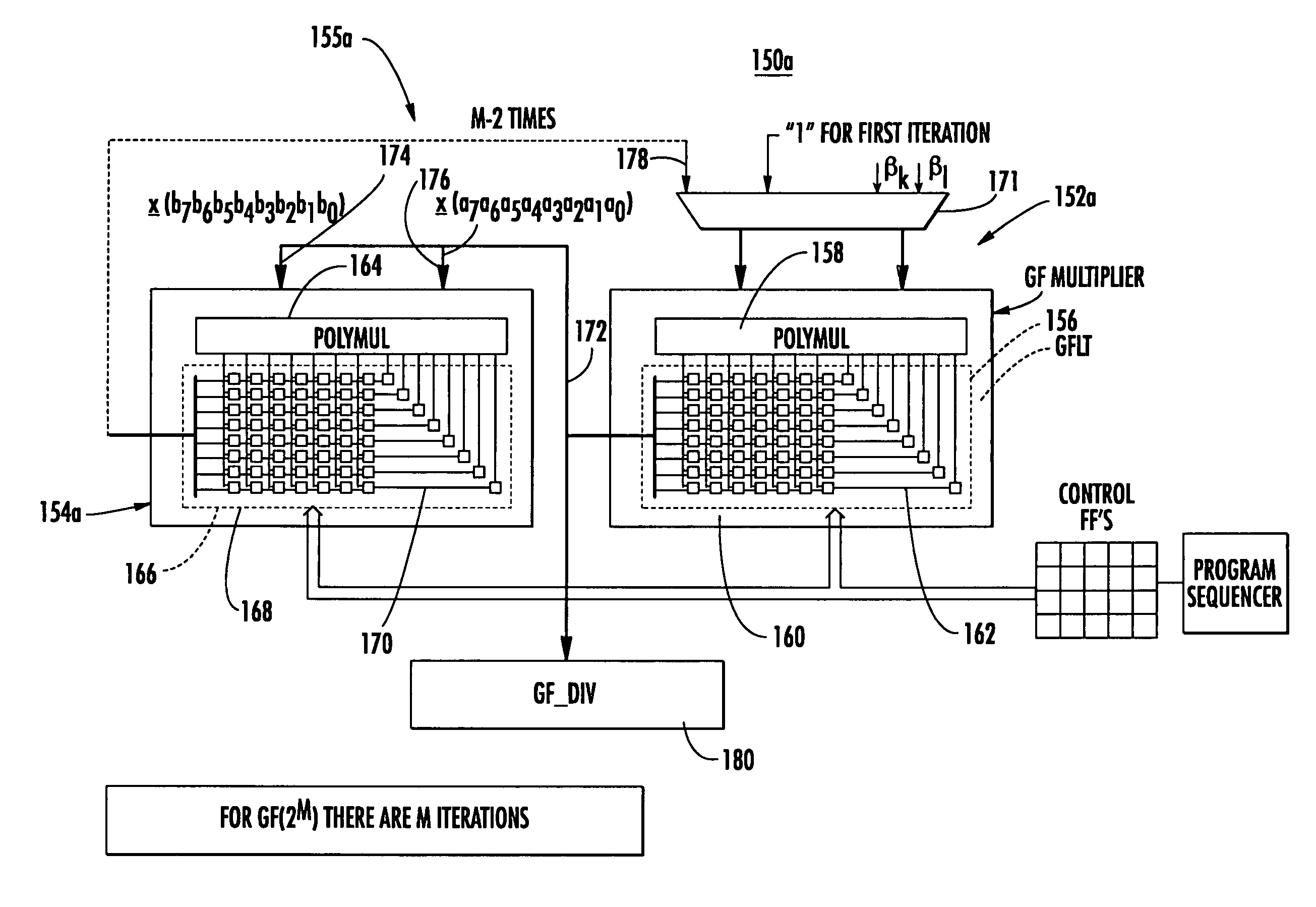
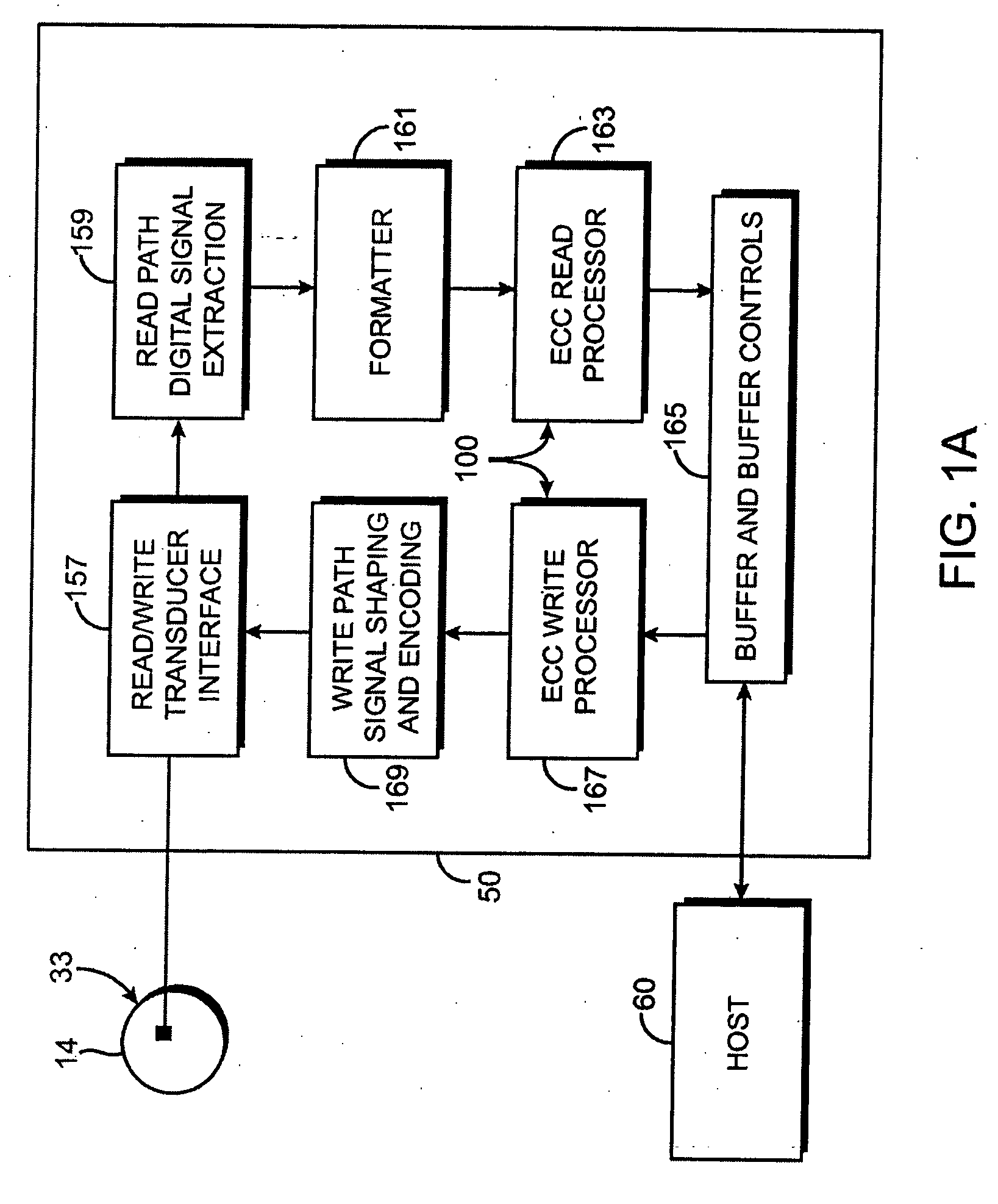
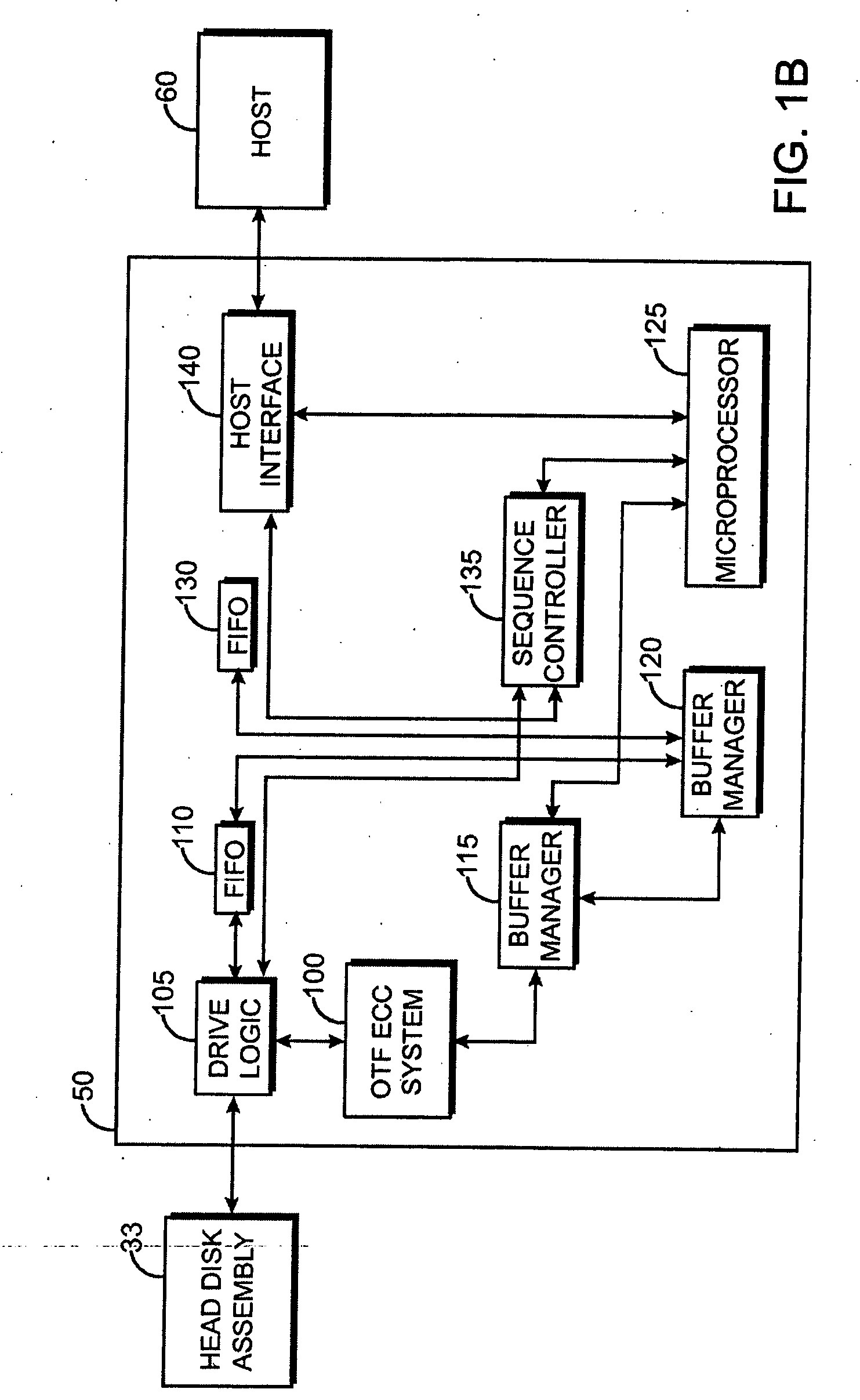
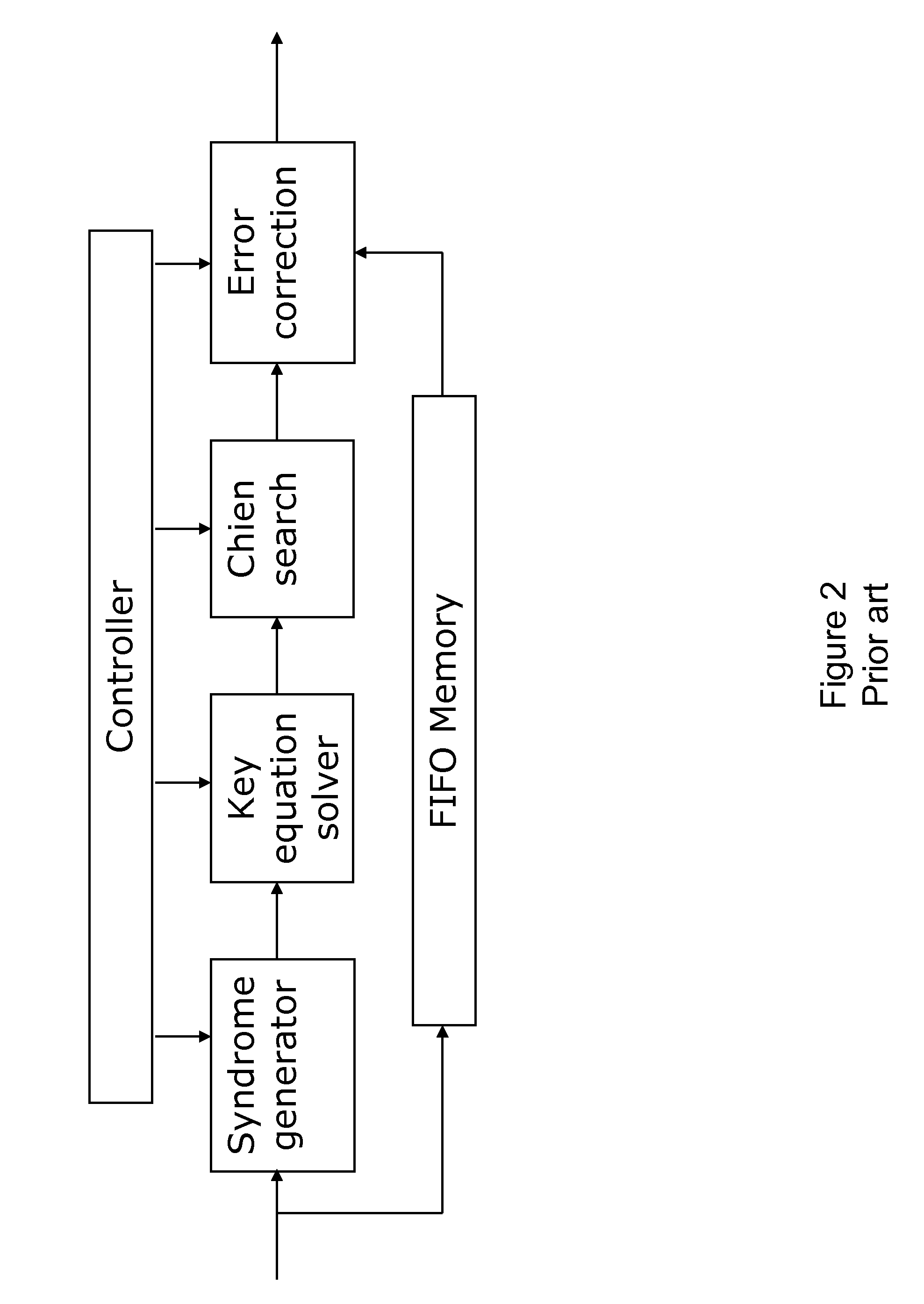
Condensed galois field computing system
InactiveUS20060123325A1Less powerReduce areaDigital data processing detailsDigital computer detailsTransformerEngineering
A condensed Galois field computing system including a multiplier circuit for multiplying first and second polynomials with coefficients over a Galois field to obtain their product; and a Galois field linear transformer circuit for applying an irreducible polynomial of power n to the product including a partial result generator responsive to terms of power n and greater in the product for providing a folded partial result and a Galois field adder for condensing the folded partial result and the terms less than power n in the product to obtain Galois field transformer of power n of the product.
Owner:ANALOG DEVICES INC
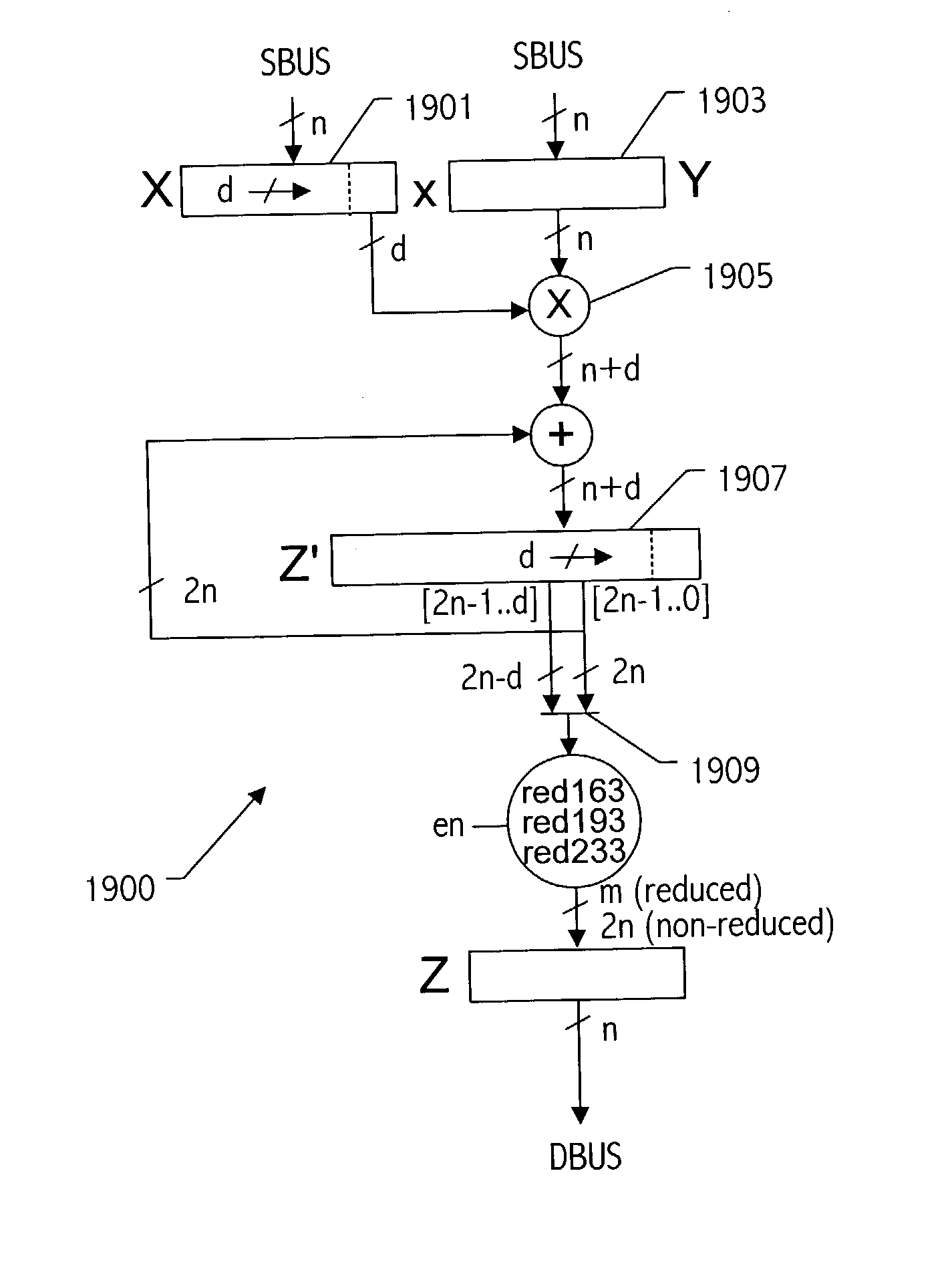
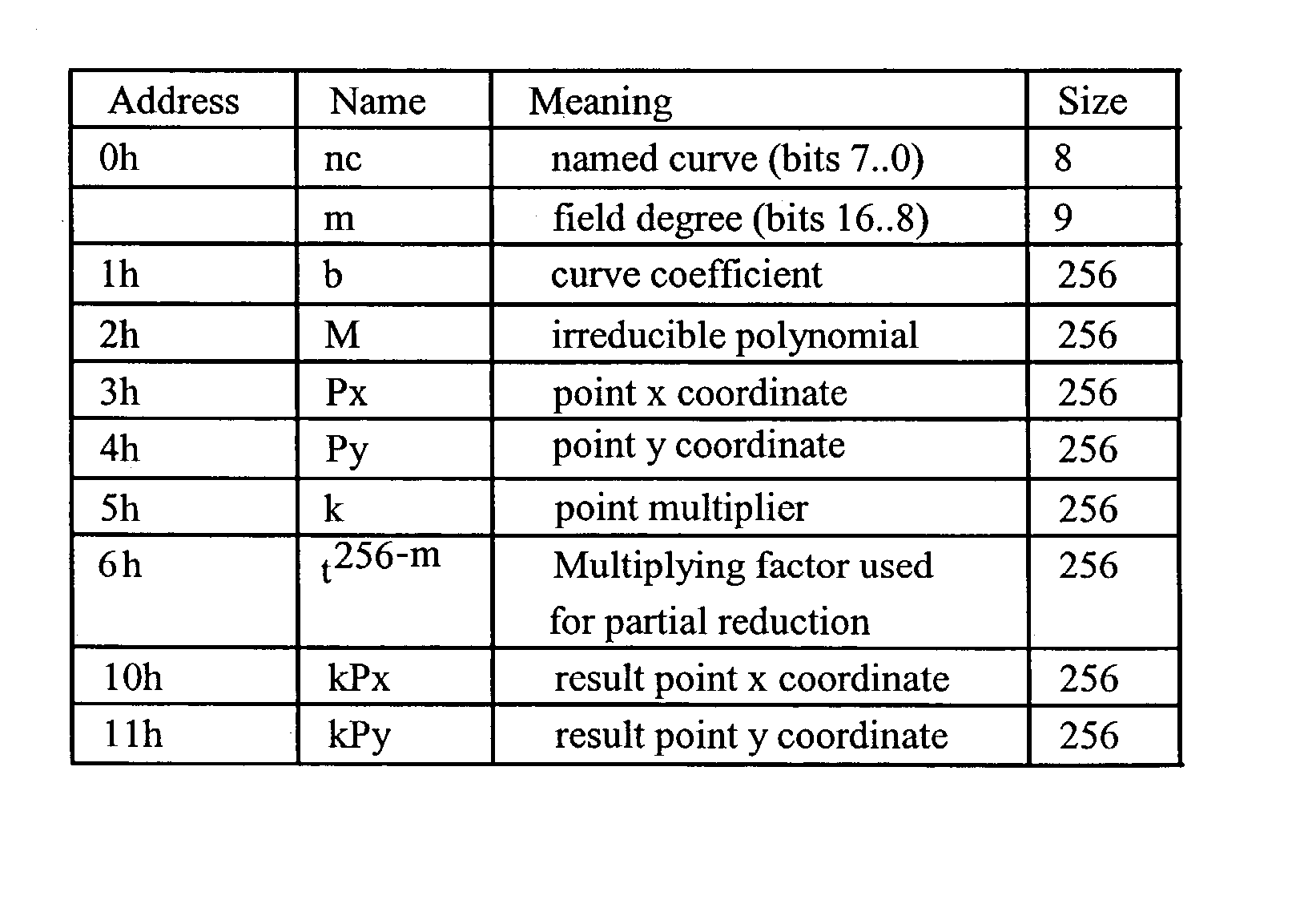
Generic implementations of ellipitic curve cryptography using partial reduction
ActiveUS20030208518A1Digital computer detailsComputations using residue arithmeticBinary multiplierOperand
A reduction operation is utilized in an arithmetic operation on two binary polynomials X(t) and Y(t) over GF(2), where an irreducible polynomial Mm(t)=t<m>+am-1t<m-1>+am-2t<m-2>+ . . . +a1t+a0, where the coefficients as are equal to either 1 or 0, and m is a field degree. The reduction operation includes partially reducing a result of the arithmetic operation on the two binary polynomials to produce a congruent polynomial of degree less than a chosen integer n, with m<=n. The partial reduction includes using a polynomial M'=(Mm(t)-t<m>)*t<n-m>, or a polynomial M''=Mm(t)*t<n-m >as part of reducing the result to the degree less than n and greater than or equal to m. The integer n can be the data path width of an arithmetic unit performing the arithmetic operation, a multiple of a digit size of a multiplier performing the arithmetic operation, a word size of a storage location, such as a register, or a maximum operand size of a functional unit in which the arithmetic operation is performed.
Owner:ORACLE INT CORP
Condensed Galois field computing system
InactiveUS7512647B2Less powerReduce areaDigital data processing detailsDigital computer detailsTransformerComputer science
A condensed Galois field computing system including a multiplier circuit for multiplying first and second polynomials with coefficients over a Galois field to obtain their product; and a Galois field linear transformer circuit for applying an irreducible polynomial of power n to the product including a partial result generator responsive to terms of power n and greater in the product for providing a folded partial result and a Galois field adder for condensing the folded partial result and the terms less than power n in the product to obtain Galois field transformer of power n of the product.
Owner:ANALOG DEVICES INC
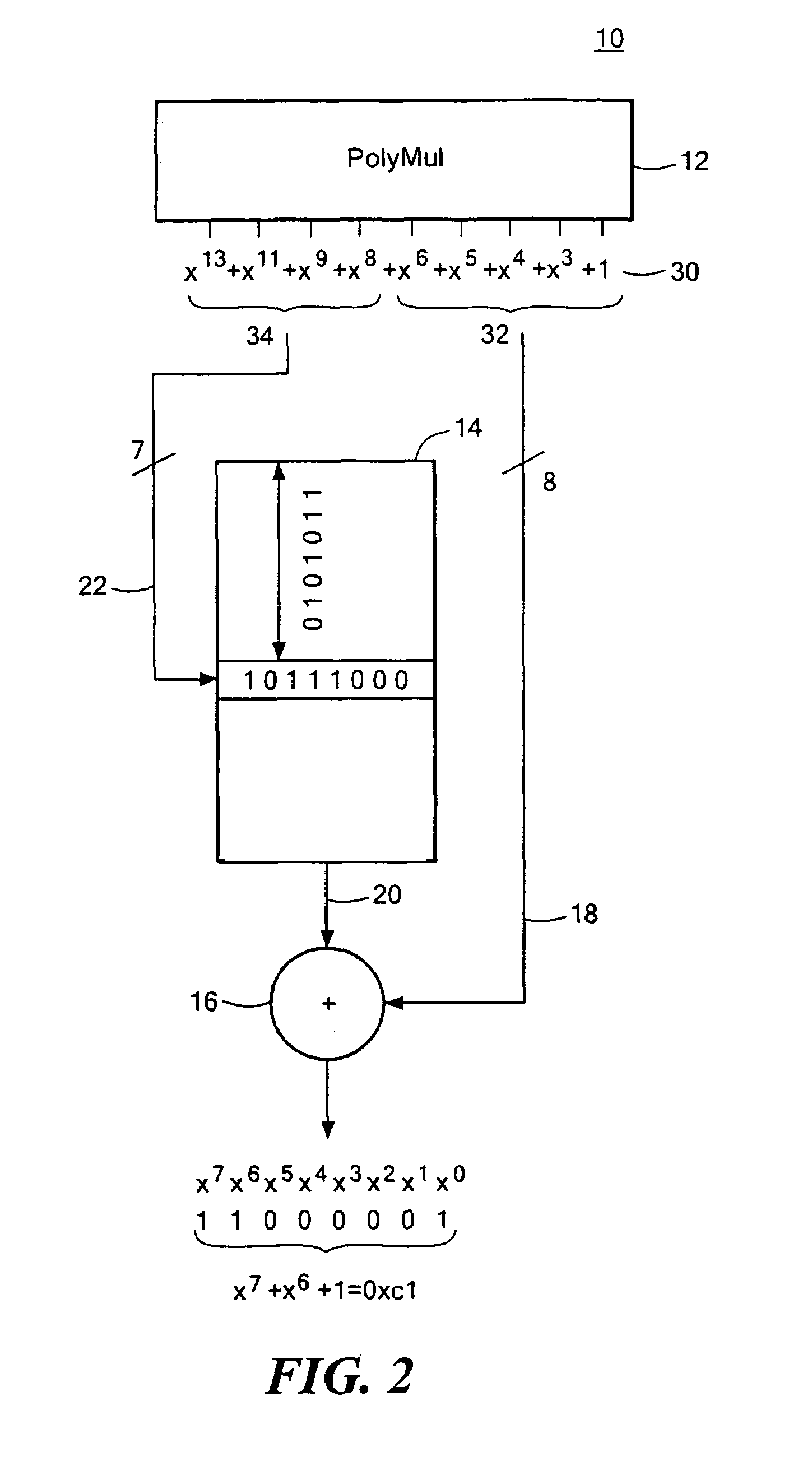
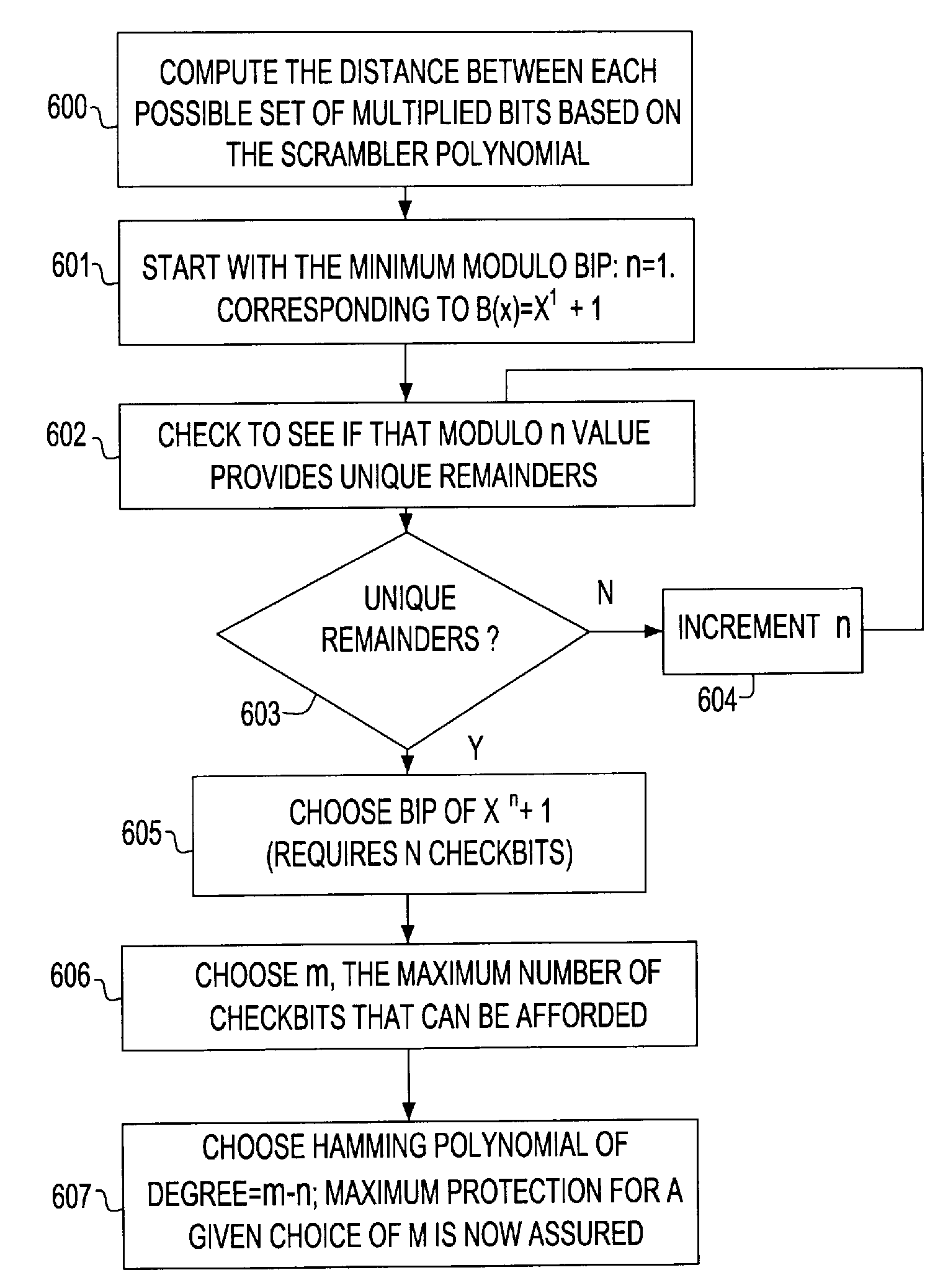
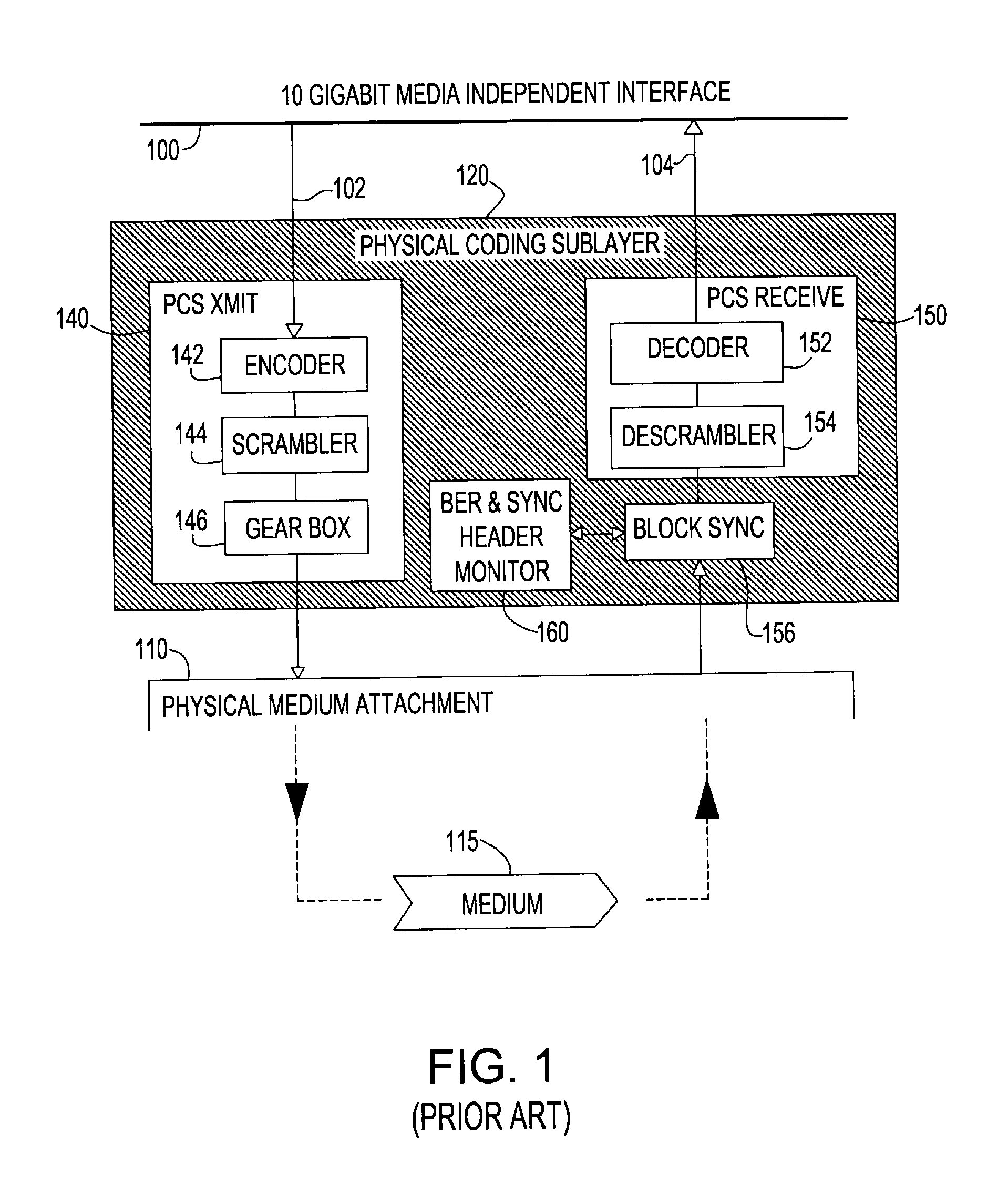
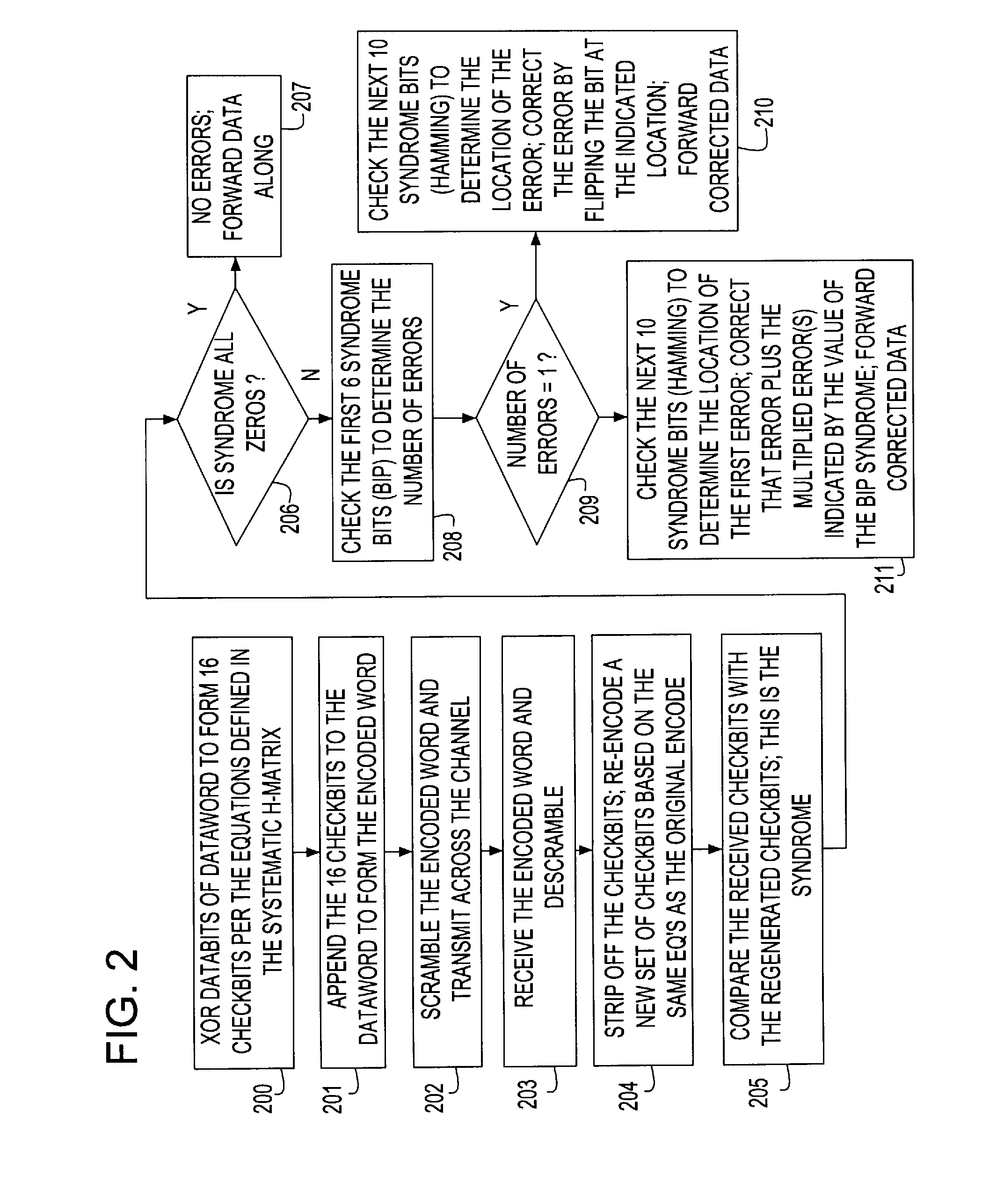
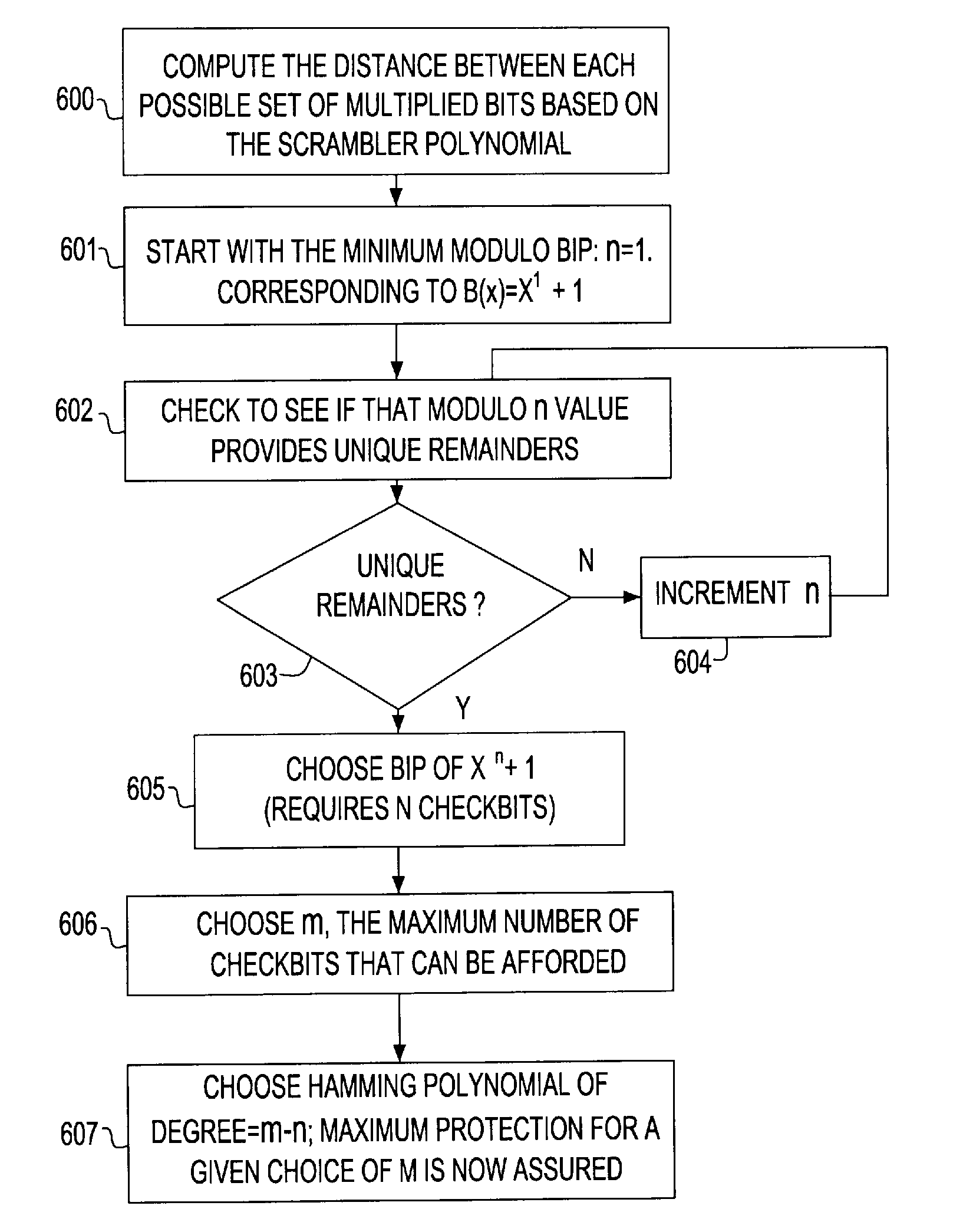
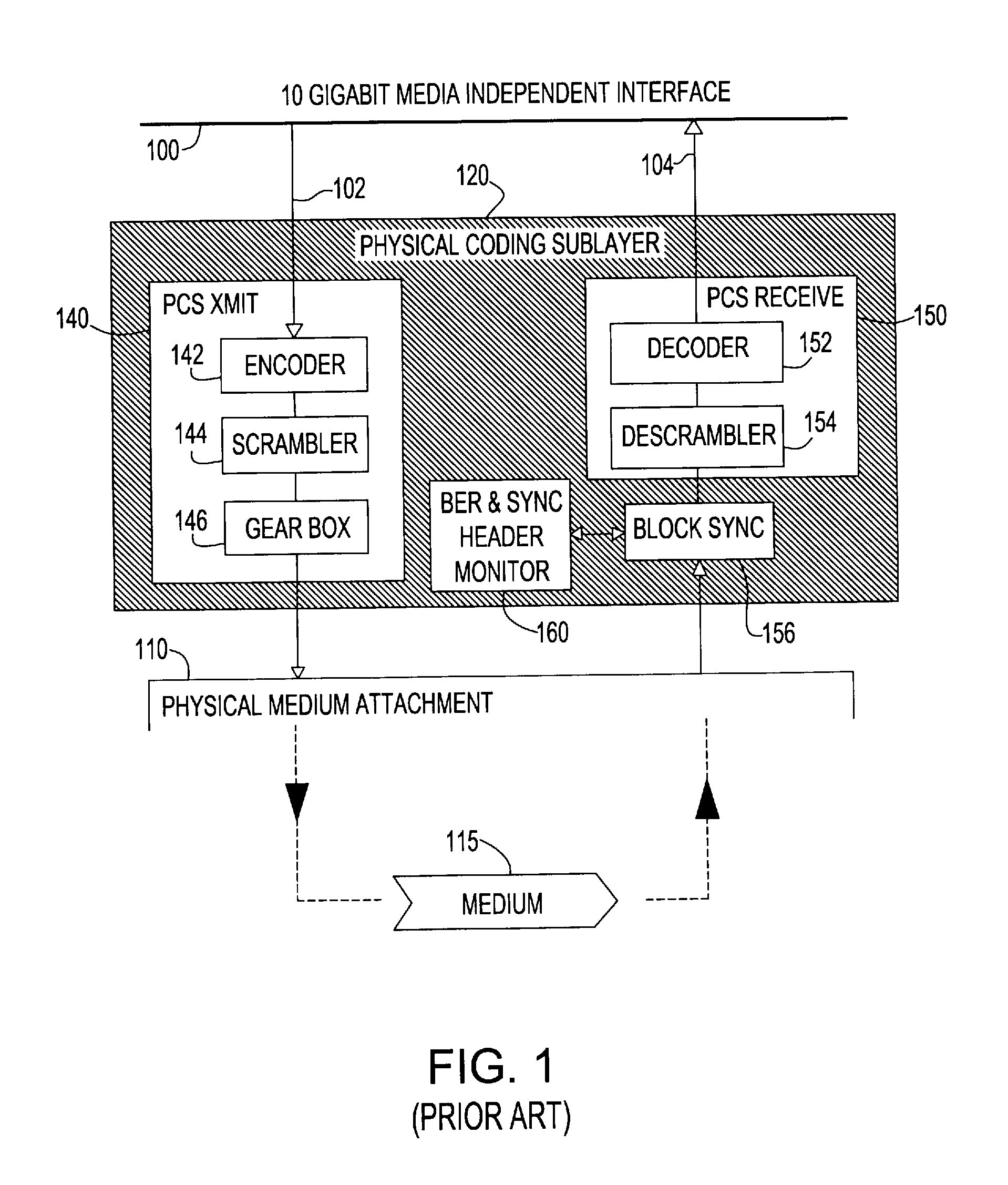
Forward error correction encoding for multiple link transmission capatible with 64b/66b scrambling
InactiveUS20080109707A1Reduce overheadCorrection errorError detection/correctionCode conversionHamming codeHigh bandwidth
Owner:IBM CORP
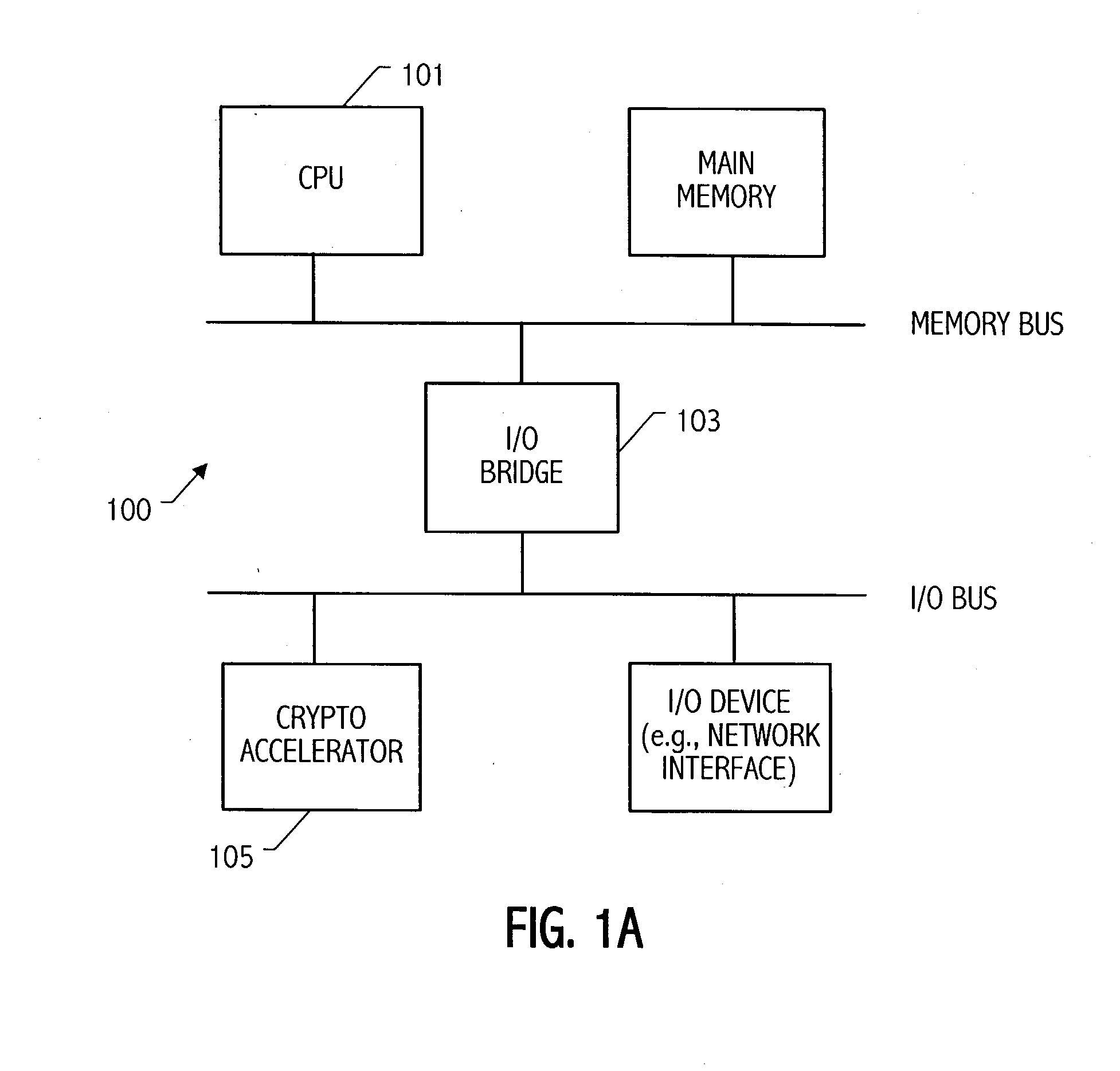
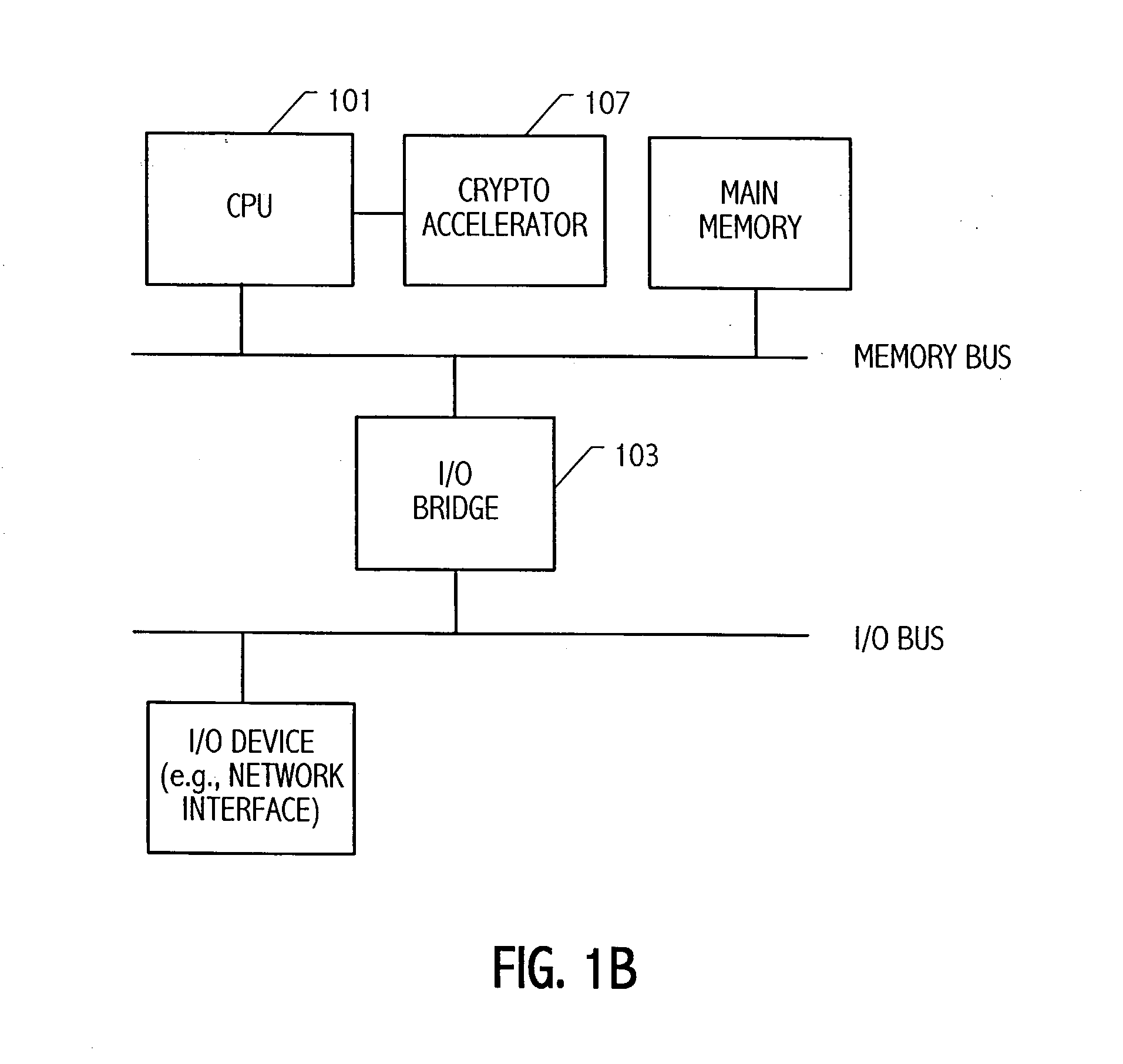
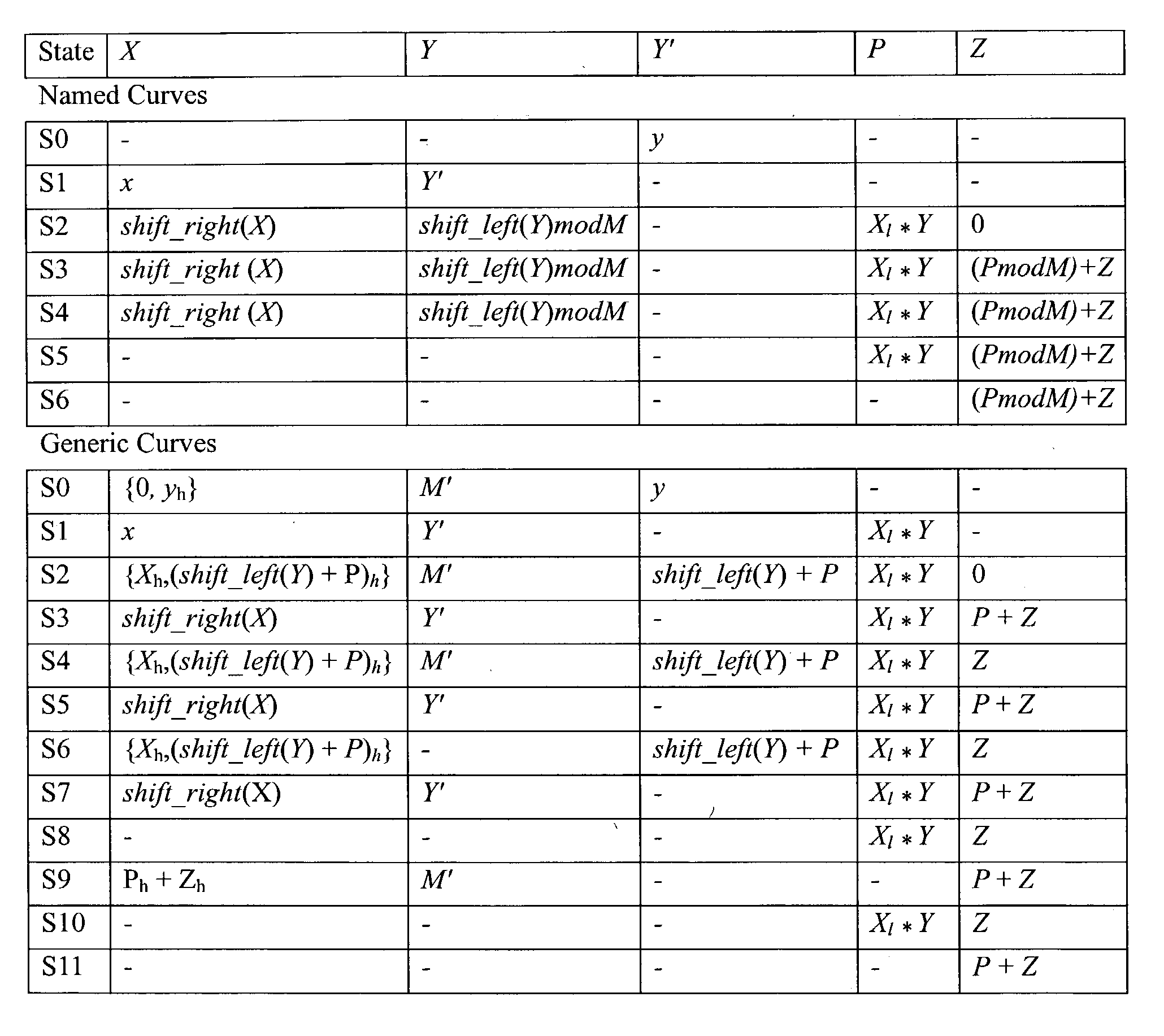
Hardware accelerator for elliptic curve cryptography
ActiveUS20030206629A1Public key for secure communicationDigital computer detailsEllipseElliptic curve cryptography
An elliptic curve processing apparatus that performs operations on elliptic curves specified over binary polynomial fields includes a functional unit that has a digit serial multiplier with a digit size of at least two bits. The elliptic curve processing apparatus performs reduction for respective generic curves using arbitrary irreducible polynomials, which correspond to respective ones of the generic curves. The elliptic curve processing apparatus may include hardwired reduction circuits in the functional unit for use with respective named curves. A storage location in the elliptic curve processing apparatus may be used to specify whether an operation is for one of the named curves or for one of the generic curves. The elliptic curve processing apparatus responds to an arithmetic instruction to utilize a respective one of the hardwired reduction circuits for reduction for respective named curves and a multiplier circuit for reduction for a plurality of generic curves, the multiplier coupled to perform reduction for respective generic curves using arbitrary irreducible polynomials, the arbitrary irreducible polynomials corresponding to respective ones of the generic curves. The elliptic curve processing apparatus operable on elliptic curves specified over binary polynomial fields performs a conditional branch according to whether a curve being processed is a generic curve or a named curve.
Owner:SUN MICROSYSTEMS INC
Forward error correction encoding for multiple link transmission compatible with 64B/66B scrambling
InactiveUS7996747B2Reduce overheadEasy to correctError detection/correctionCode conversionHamming codeHigh bandwidth
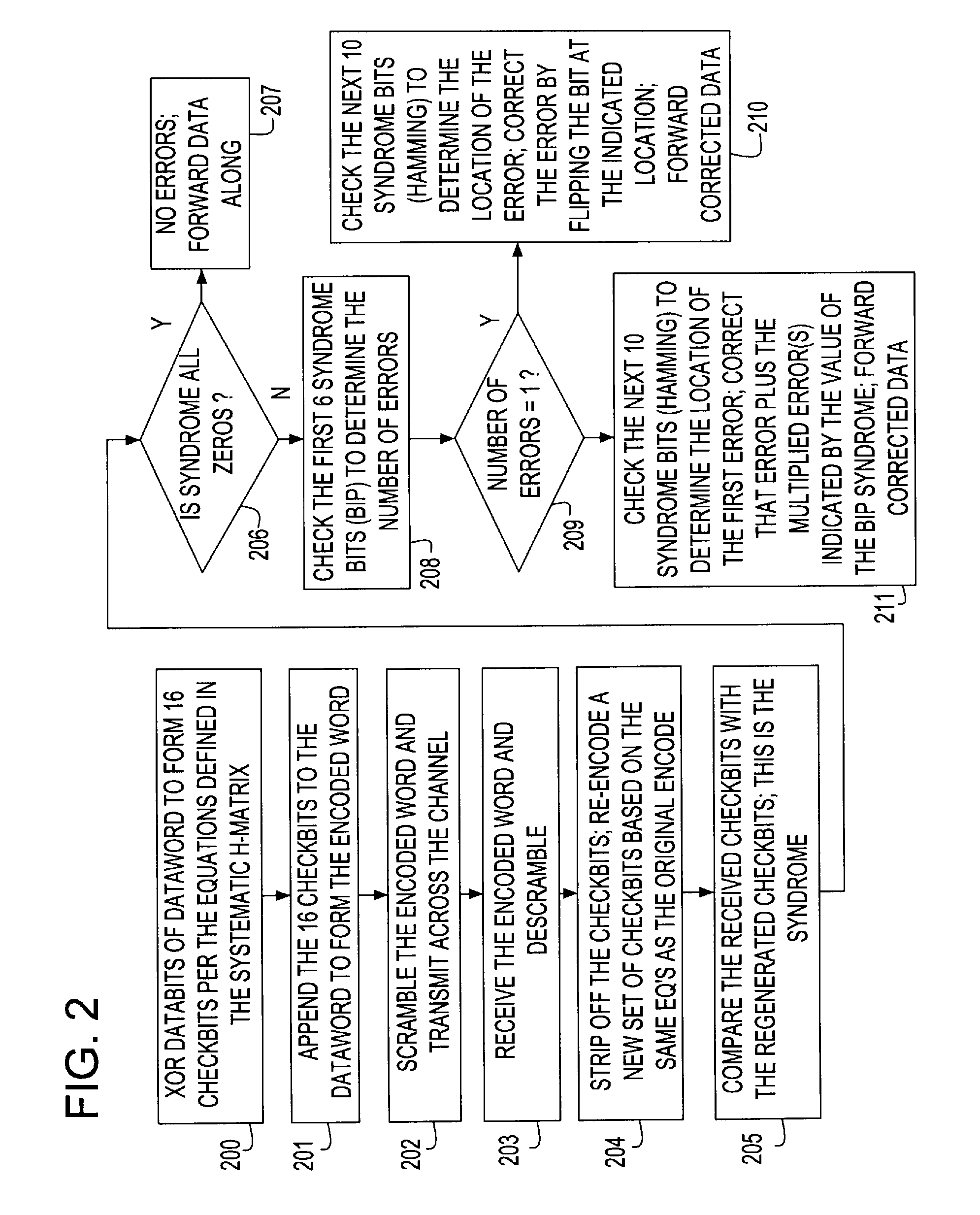
A Forward Error Correction (FEC) code compatible with the self-synchronized scrambler used by the 64B / 66B encoding standard for transmission on Serializer / Deserializer (SerDes) communications channel links. The FEC code allows encoding and decoding to occur before and after scrambling, respectively, so as to preserve the properties of the scrambling operation on the transmitted signal. The code allows the correction of any single transmission error in spite of the multiplication by three of all transmission errors due to the 64B / 66B scrambling process. A Hamming code is combined with a Bit Interleaved Parity code of degree n (BIP-n). These two codes provide for protection both for an error anywhere in the maximum length of the packet as well as for an error replicated two or three times by the descrambling process. All single bit errors, whether multiplied or not, have unique syndromes and are therefore easily correctable. In addition, the packet can be transported across multiple serial links for higher bandwidth applications without a degradation of the code efficiency. The Hamming code can be generated from any irreducible polynomial, such as H(x)=x10+x3+1. The BIP code is chosen to be of degree 6 to fit with 64B / 66B scrambling polynomial and is represented by B(x)=x6+1.
Owner:INT BUSINESS MASCH CORP
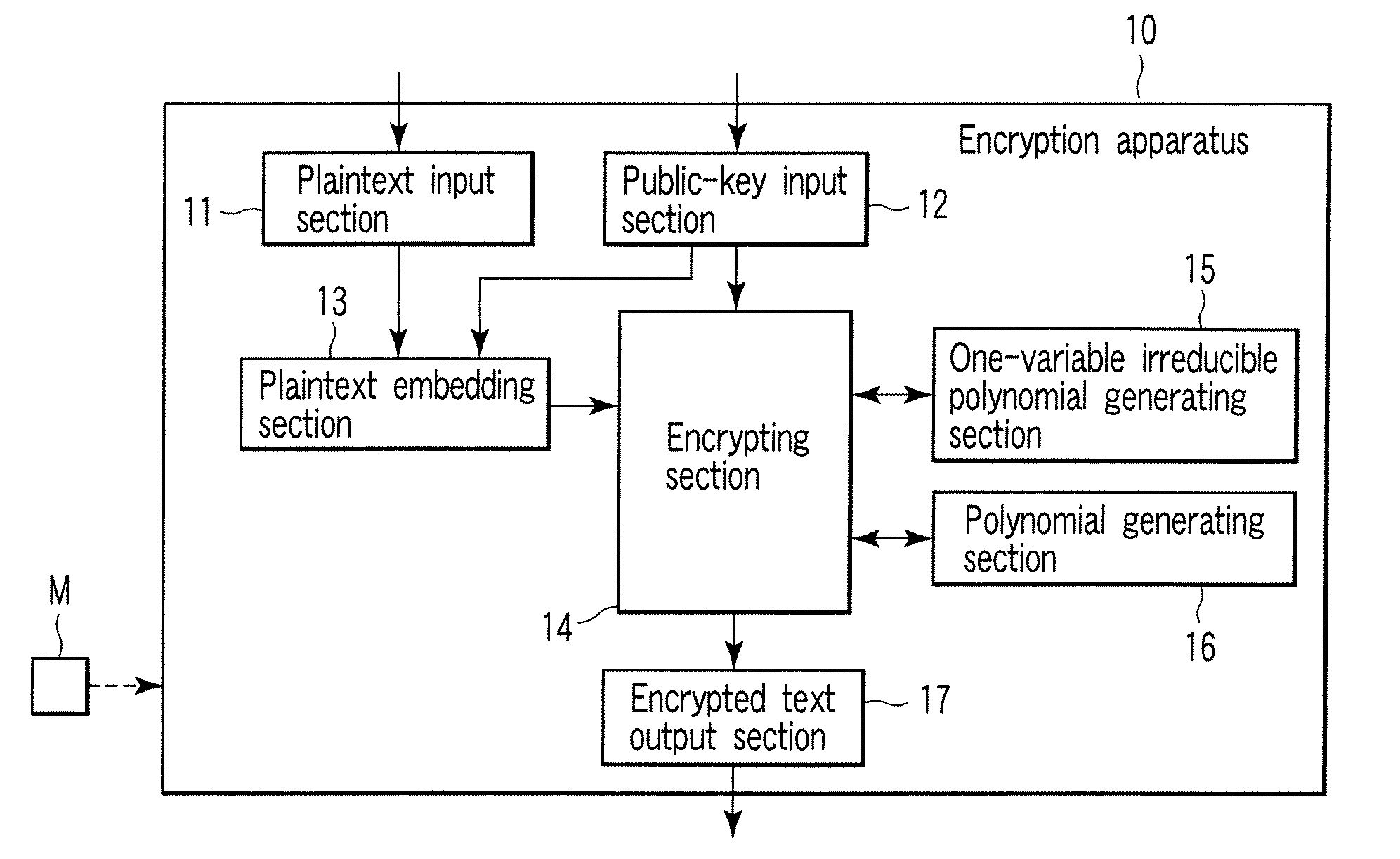
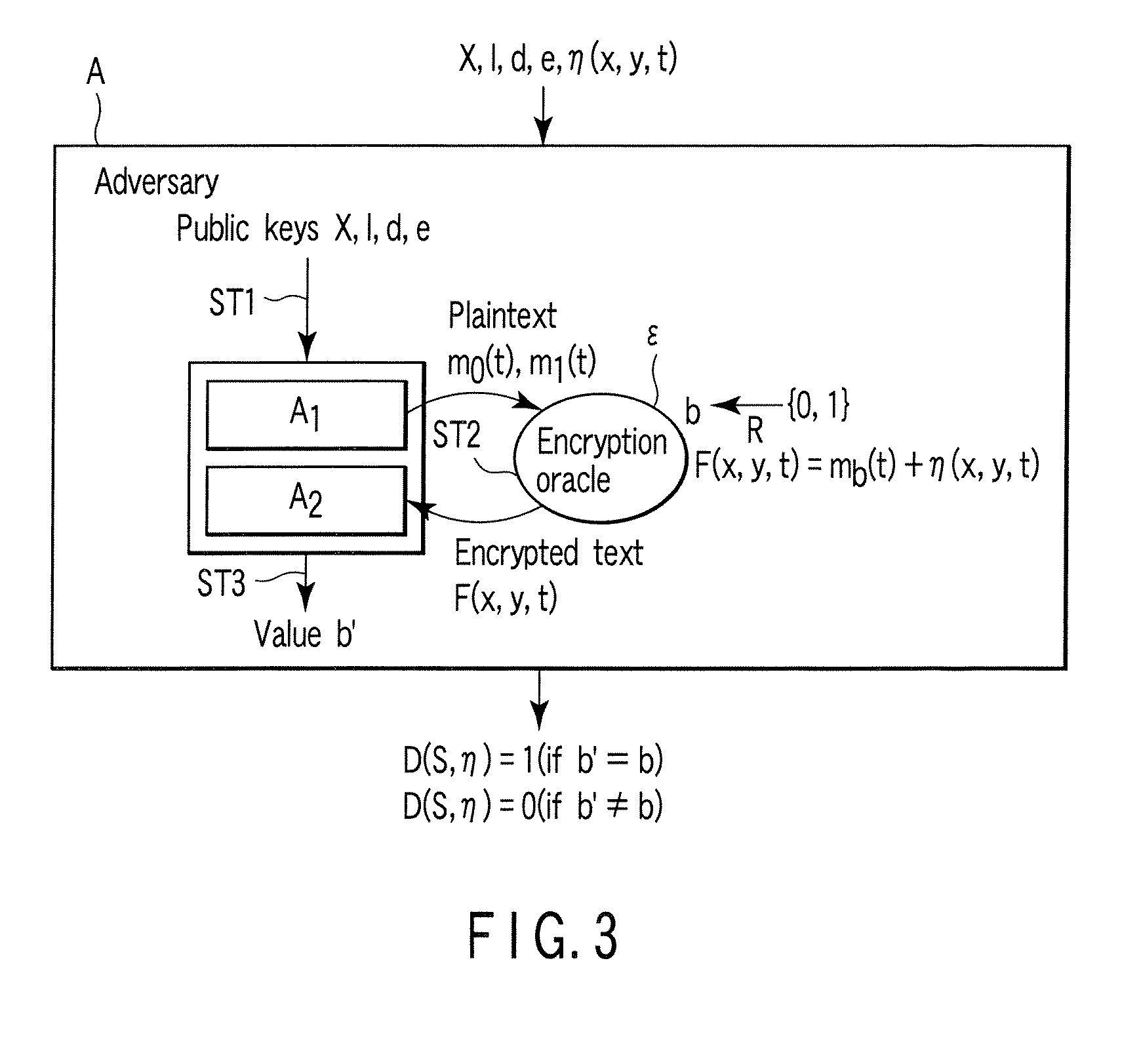
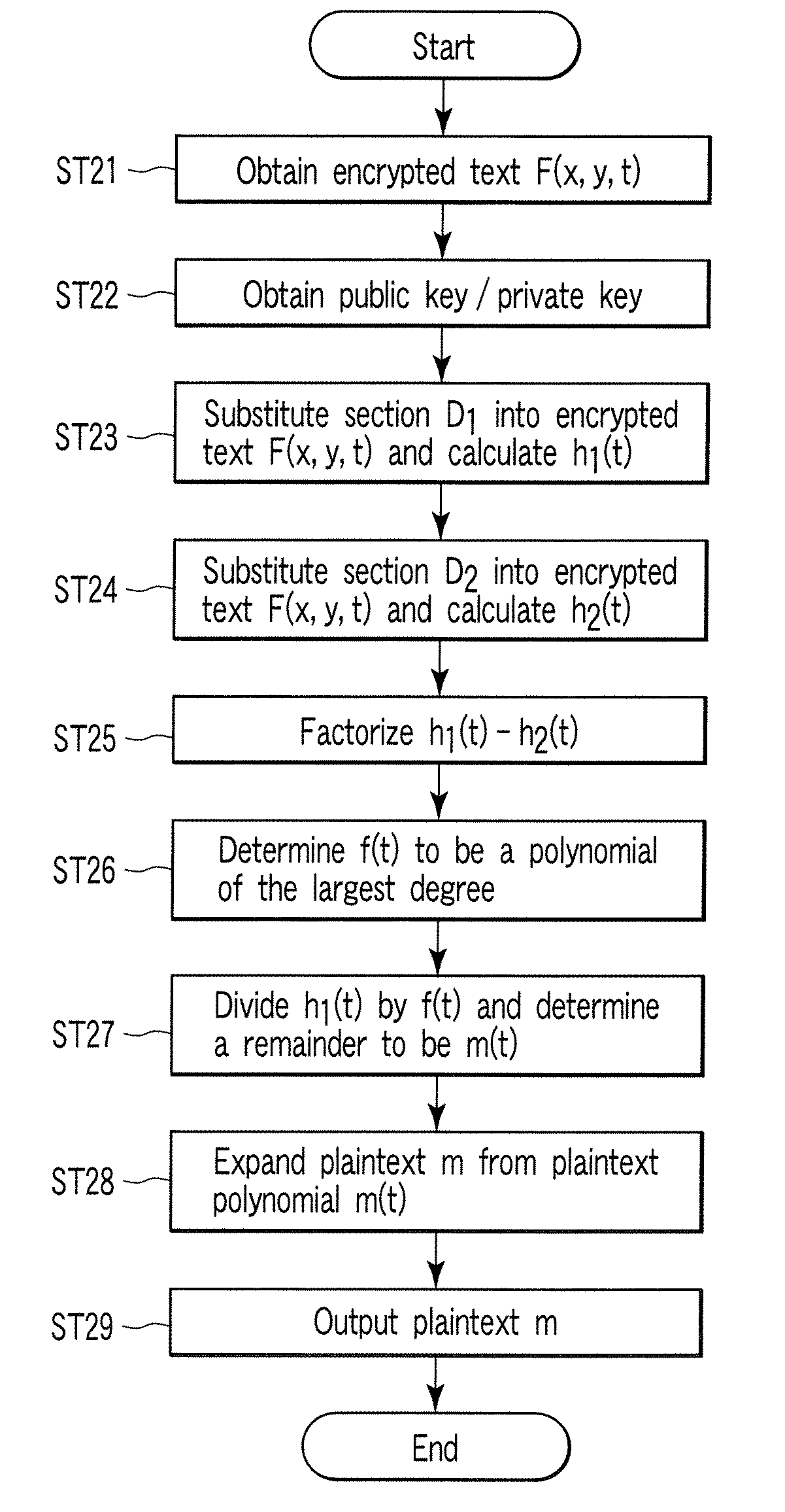
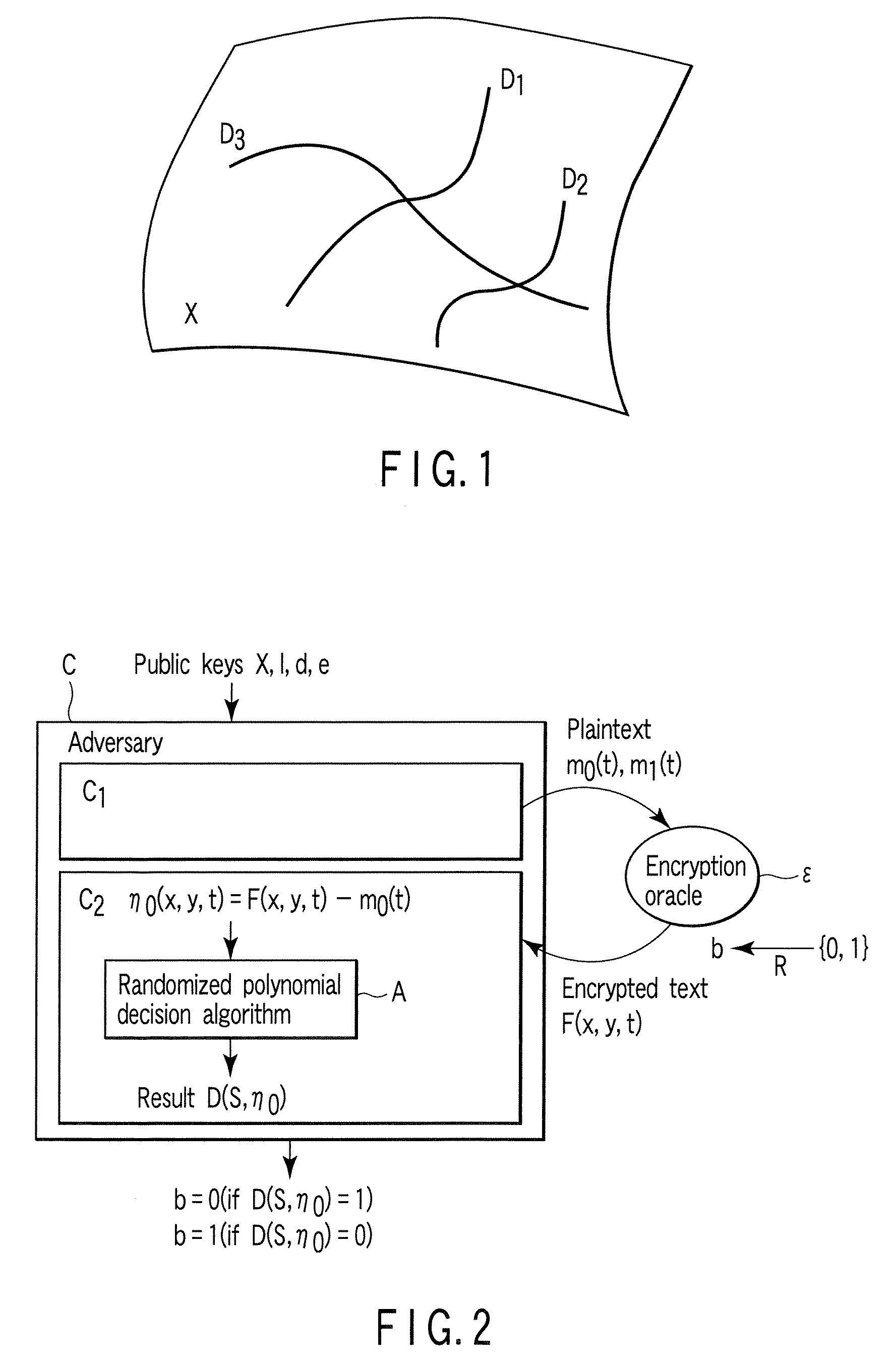
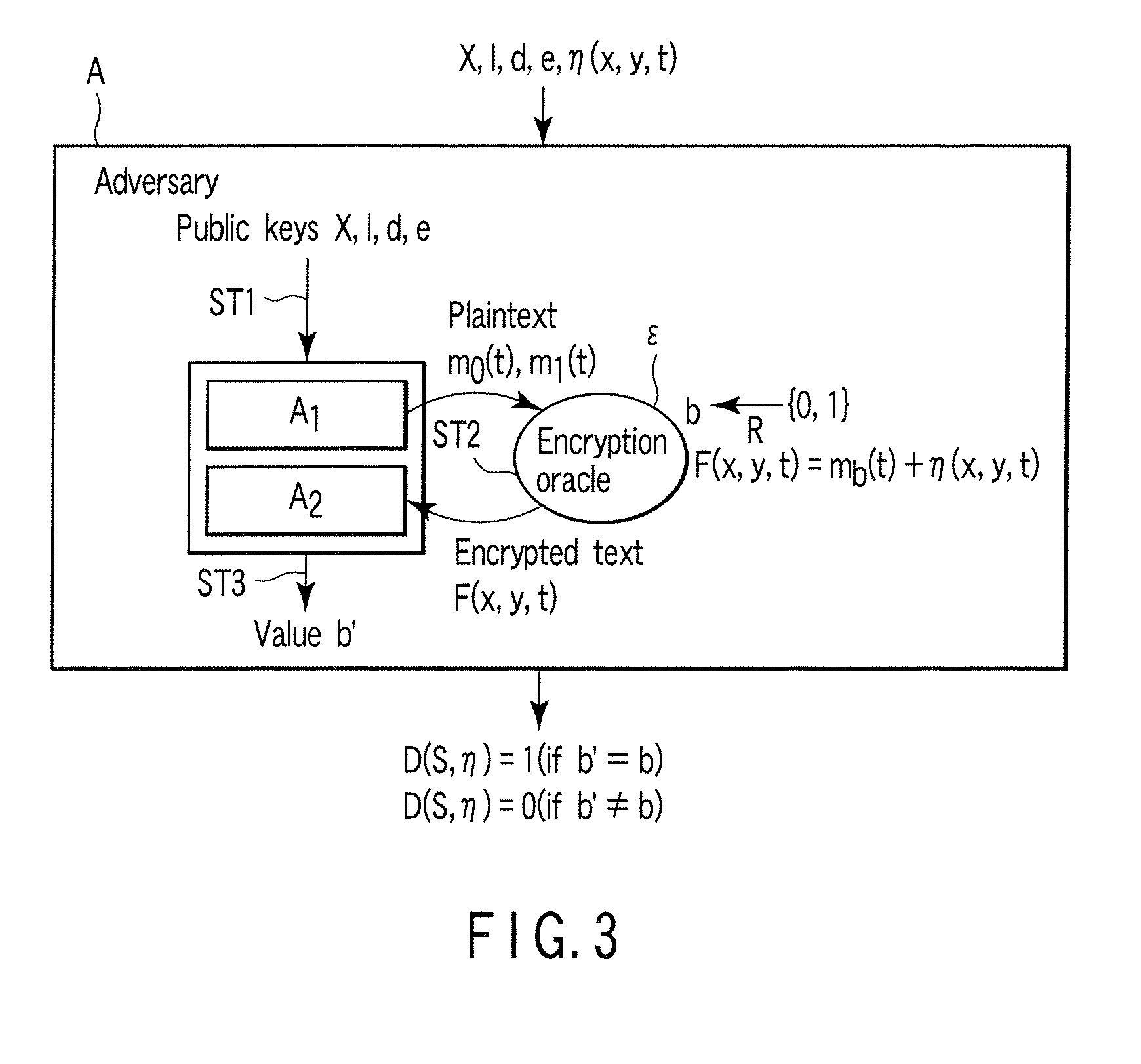
Encryption apparatus, decryption apparatus, and method
InactiveUS20070110232A1Public key for secure communicationUser identity/authority verificationPlaintextComputer hardware
A method whereby an encryption apparatus encrypts a message on the basis of a fibration X(x, y, t) serving as a public key when private keys are two or more sections corresponding to fibration X(x, y, t)=0 of an algebraic surface X, the method comprises embedding plaintext M obtained by concatenating the message to a random number as the coefficients of plaintext polynomial M(t) of degree l−1 or less, and generating encrypted text F=Epk(M, p, q, f, X) from the plaintext polynomial M(t) by an encrypting process of performing operations including at least one of addition, subtraction, and multiplication of random polynomials p(x, y, t), q(x, y, t), a random irreducible polynomial f(t) of degree l or more, and the fibration X(x, y, t) with respect to the plaintext polynomial M(t).
Owner:KK TOSHIBA
Generic modular multiplier using partial reduction
ActiveUS20030206628A1Public key for secure communicationDigital computer detailsBinary multiplierParallel computing
An apparatus multiplies a first and a second binary polynomial X(t) and Y(t) over GF(2), where an irreducible polynomial Mm(t)=t<m>+am-1t<m-1>+am-2t<m-2>t<m-2>+ . . . +a1t+a0, and where the coefficients ai are equal to either 1 or 0, and m is a field degree. The degree of X(t)<n, and the degree of Y(t)<n, and m<=n. The apparatus includes a digit serial modular multiplier circuit coupled to supply a multiplication result of degree >=m of a multiplication of the first and second binary polynomials. The digit serial modular multiplier circuit includes a first and second register, each being <=n bits. A partial product generator circuit multiplies a portion of digit size d of contents of the first register and contents of the second register. The partial product generator is also utilized as part of a reduction operation for at least one generic curve.
Owner:ORACLE INT CORP
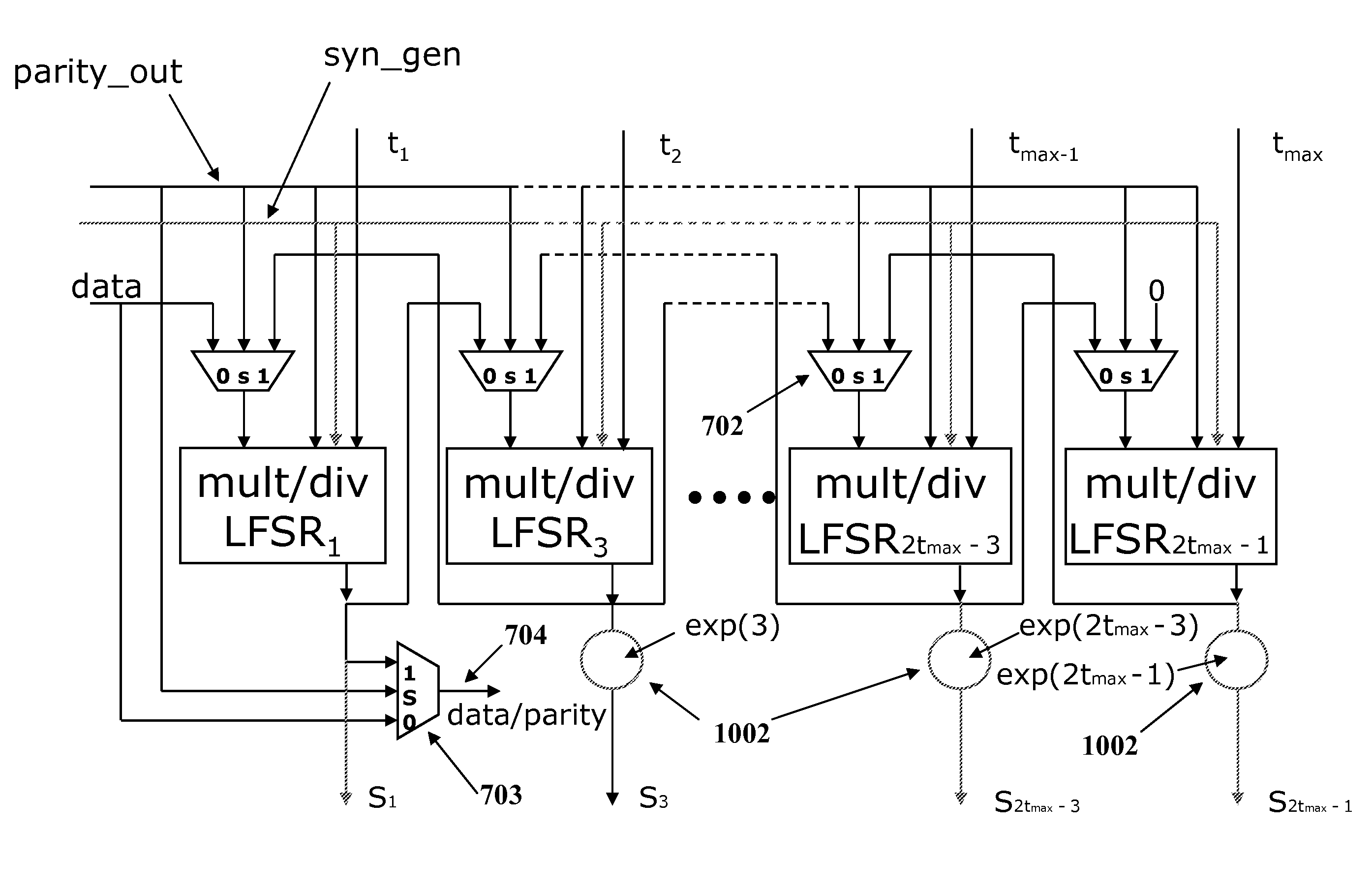
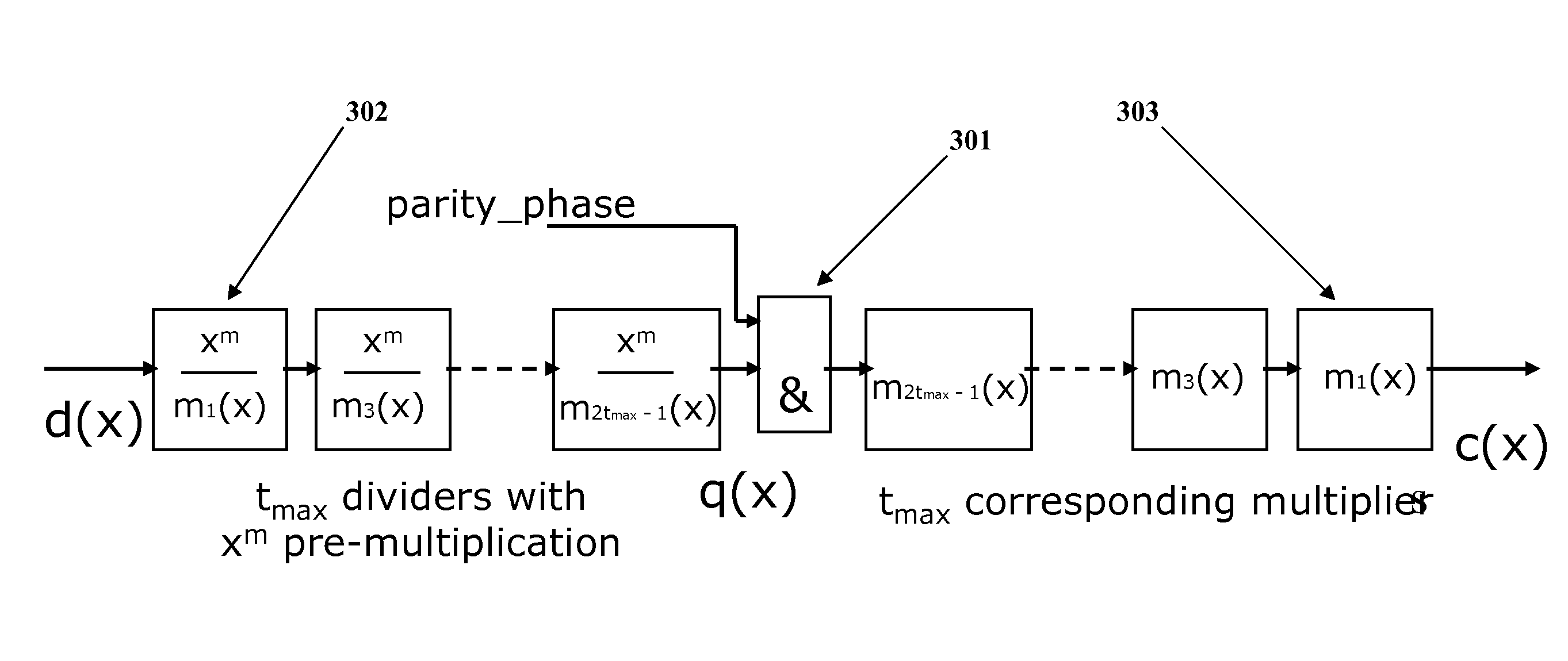
Programmable Error Correction Capability for BCH Codes
An embodiment of the invention relates to a BCH encoder formed with linear feedback shift registers (LFSRs) to form quotients and products of input polynomials with irreducible polynomials of a generator polynomial g(x) of the BCH encoder, with and without pre-multiplication by a factor xm. The BCH encoder includes multiplexers that couple LFSR inputs and outputs to other LFSRs depending on a data input or parity generation state. The BCH encoder can correct up to a selectable maximum number of errors in the input polynomials. The BCH encoder further includes LFSR output polynomial exponentiation processes to produce partial syndromes for the input data in a syndrome generation state. In the syndrome generation state the LFSRs perform polynomial division without pre-multiplication by the factor xm. The exponentiation processes produce partial syndromes from the resulting remainder polynomials of the input data block.
Owner:INFINEON TECH AG
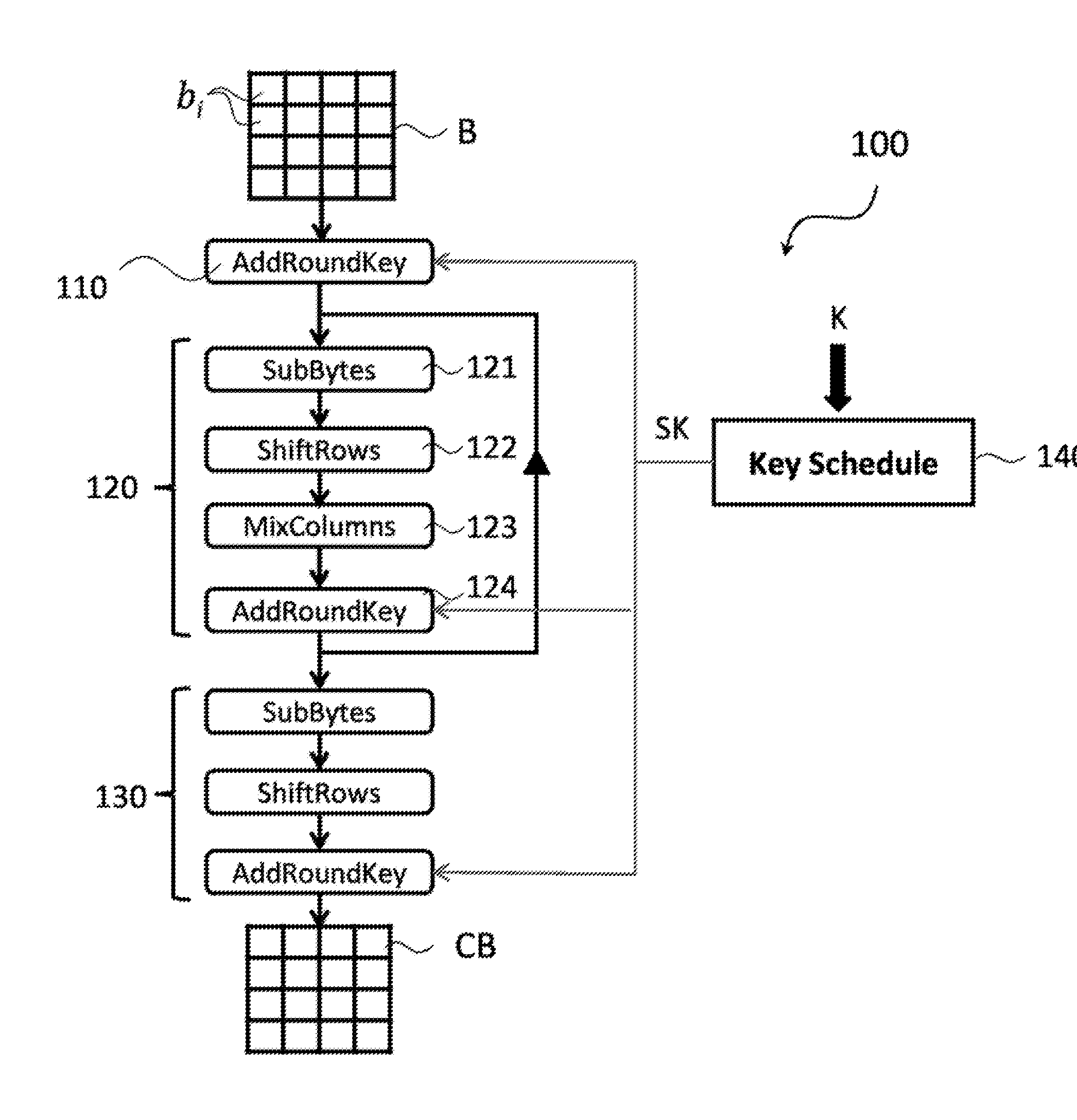
Method for performing an encryption of an aes type, and corresponding system and computer program product
ActiveUS20150270967A1Improve securityMultiple keys/algorithms usagePublic key for secure communicationChinese remainder theoremTheoretical computer science
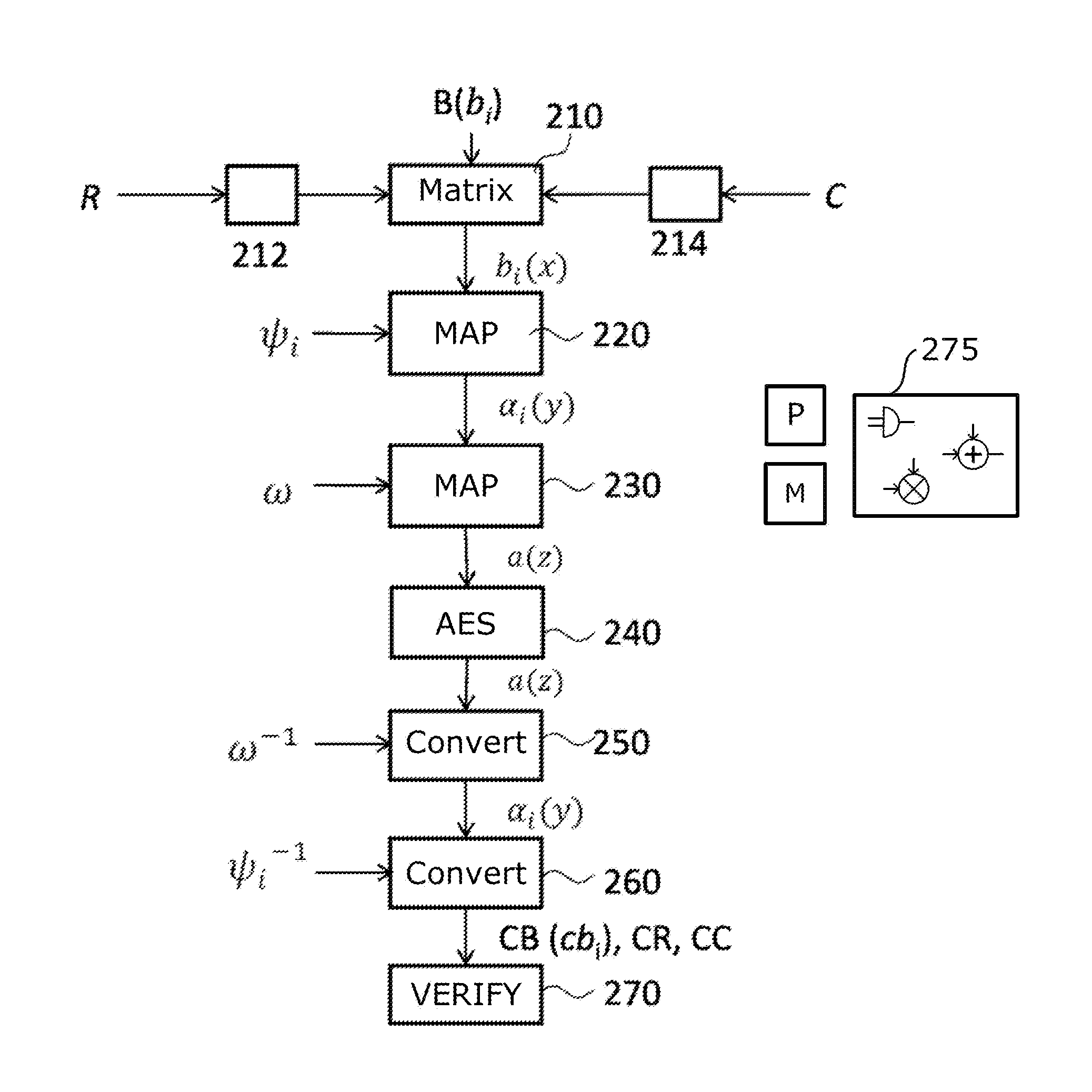
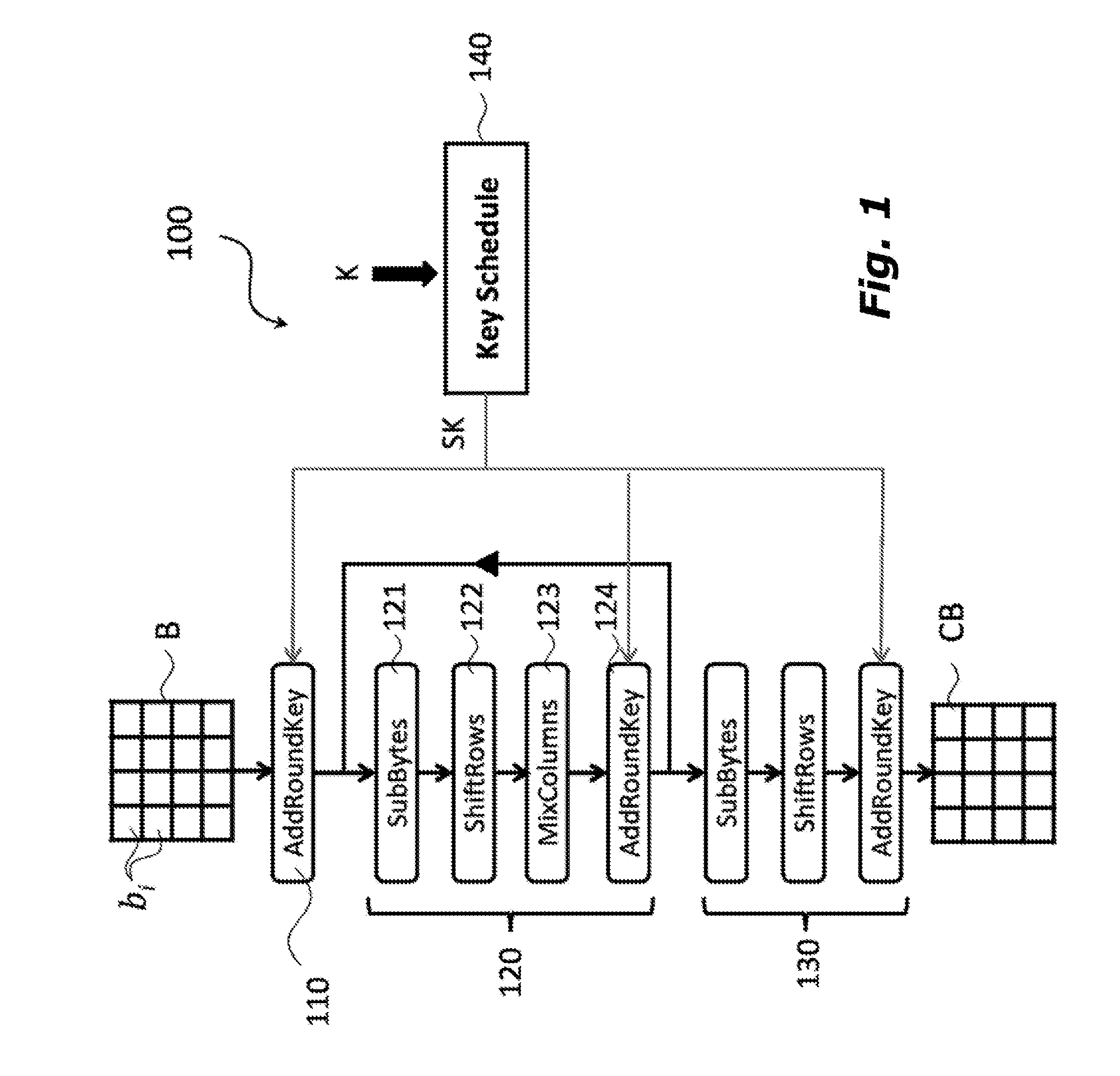
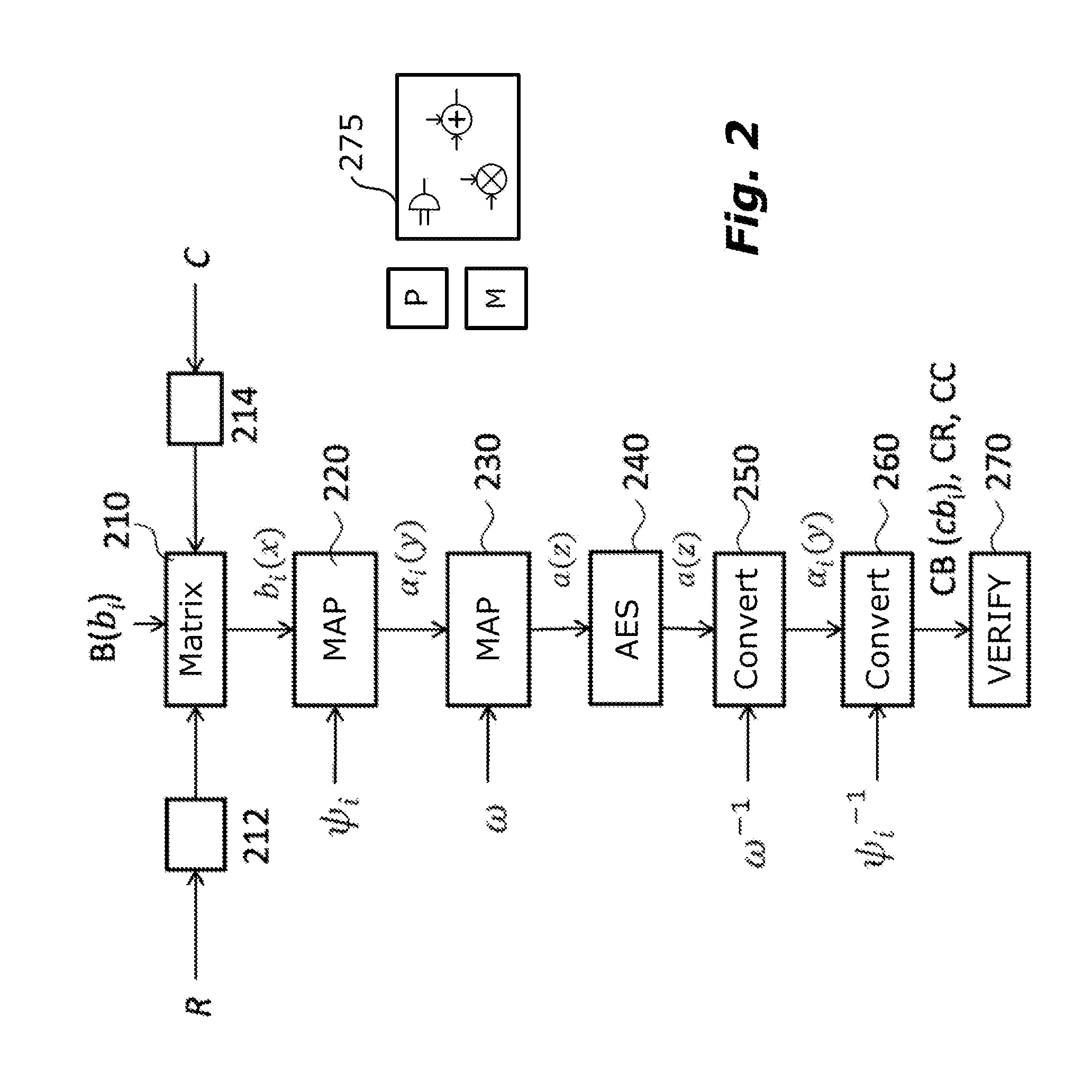
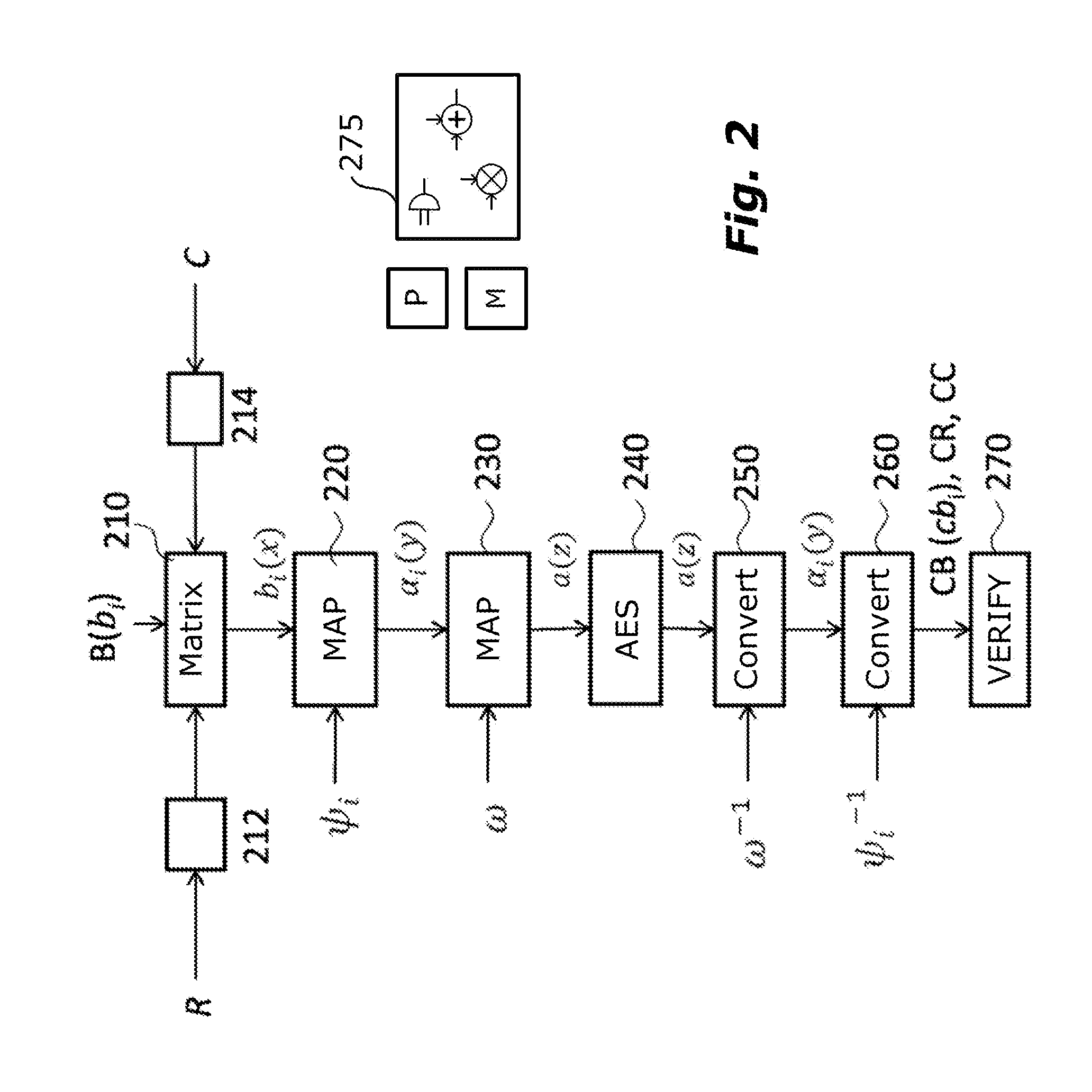
A polynomial representation (bi(x)) in an AES finite field(Z2[x](r(x)))of input bytes (bi) of a state matrix (B) is obtained. A plurality (1) of irreducible polynomials (fi(y)) and a moving map (ψi) are used to map each polynomial (bi(x)) of the polynomial representation into a respective field of polynomials(Z2[y](fi(y)))computed with respect to one of the irreducible polynomials (fi(y)), to obtain respective moved polynomials (αi(y)). The moved polynomials (αi(y)) are mapped into a polynomial (a(z)) of a polynomial ring(Z2[z](p(z))),obtained by applying an isomorphism (ω) between the fields of polynomials(Z2[y](fi(y)))and the polynomial ring(Z2[z](p(z)))based upon the Chinese remainder theorem (CRT). AES encryption is applied to the polynomial (a(z)). The polynomial (a(z)) is reconverted into the AES finite field(Z2[x](r(x)))to obtain an encrypted state matrix (CB).
Owner:STMICROELECTRONICS SRL
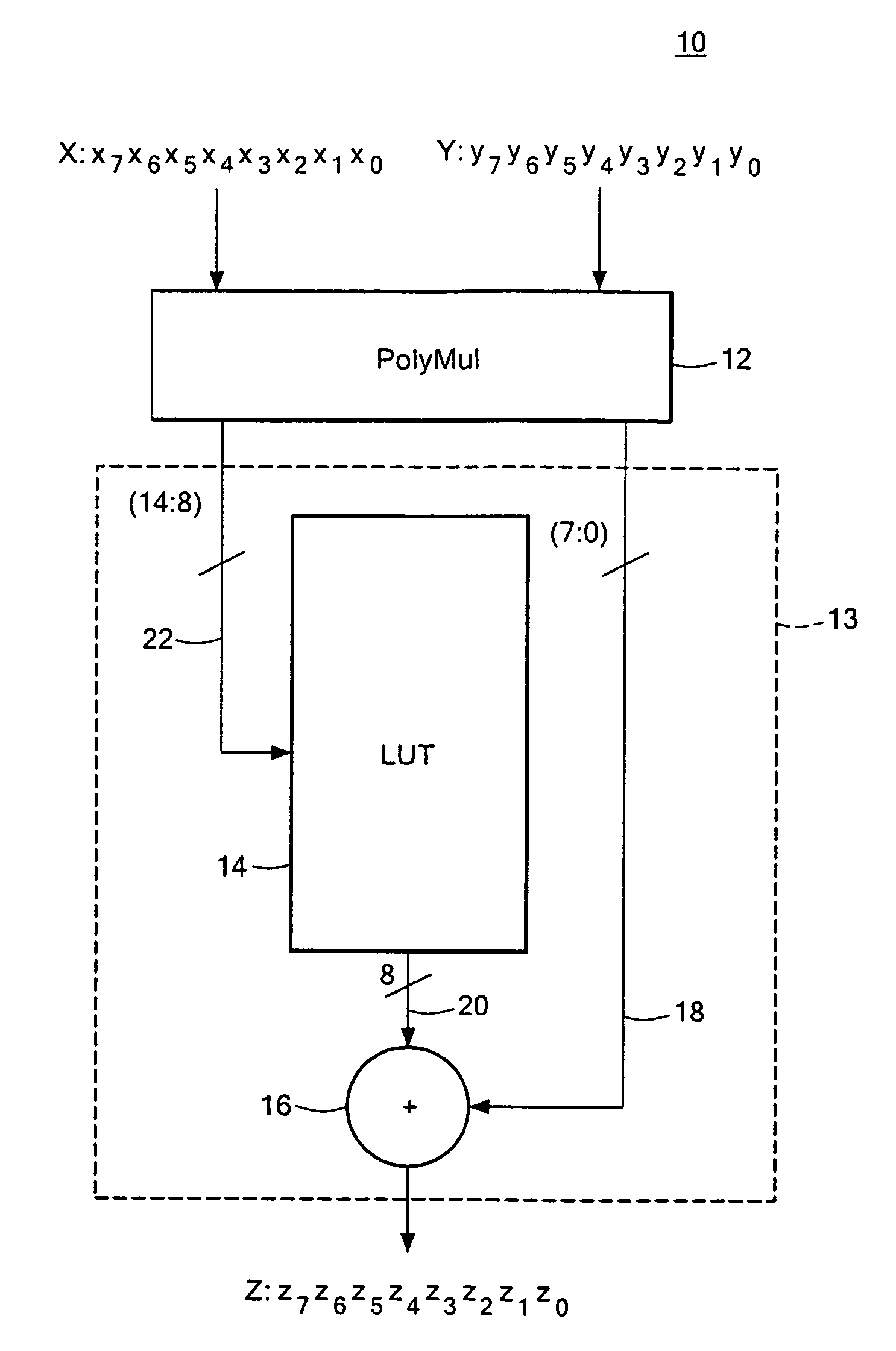
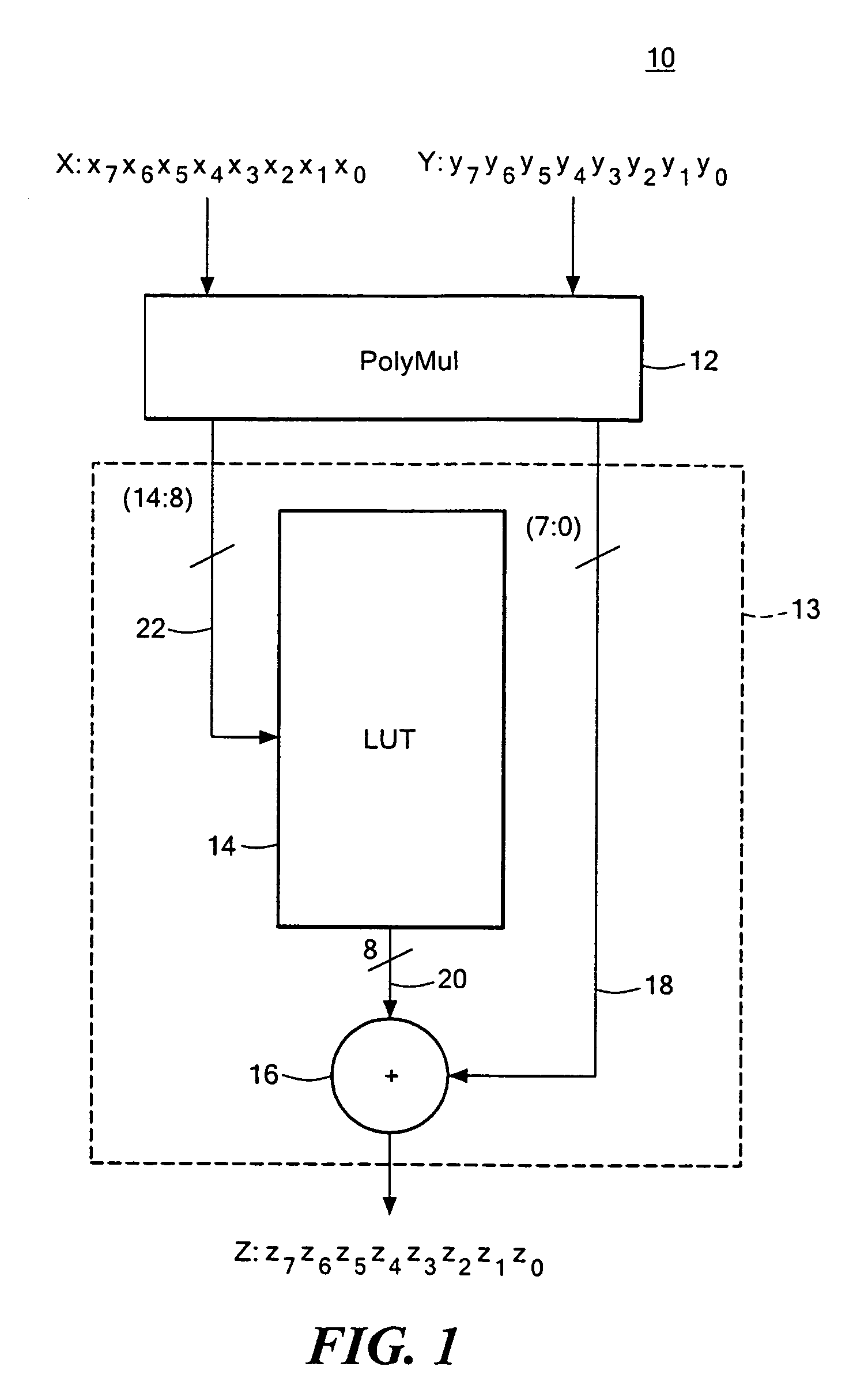
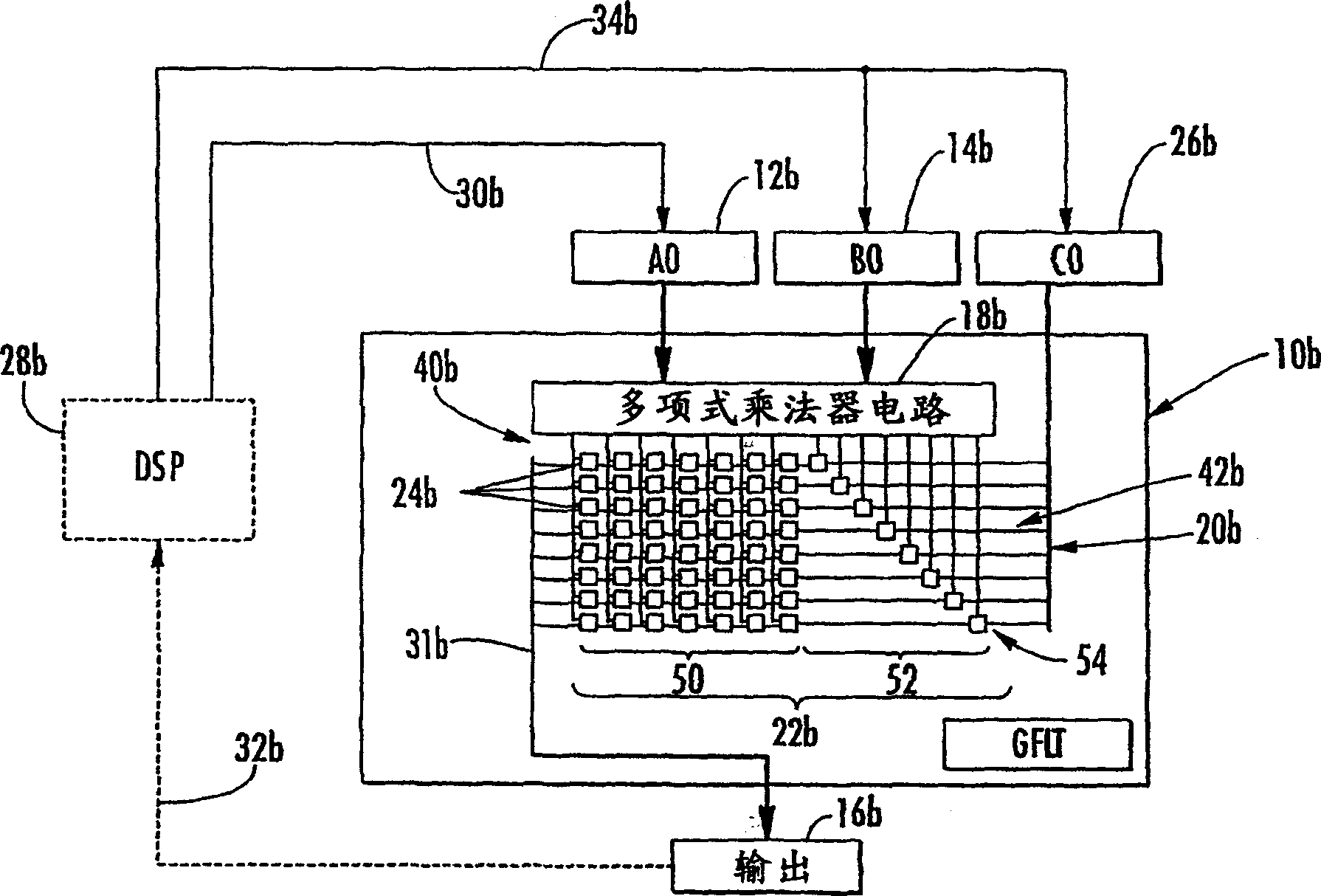
Compact Galois field multiplier engine
InactiveUS7177891B2Shorten the propagation pathSmall sizeComputation using non-contact making devicesDigital computer detailsBinary multiplierTransformer
A compact Galois field parallel multiplier engine includes a multiplier circuit for multiplying together two polynomials with coefficients over a Galois field to obtain their product; a Galois field linear transformer circuit has a multiply input from the multiplier circuit for predicting the modulo remainder of the polynomial product for an irreducible polynomial; first and second polynomial inputs; the Galois field linear transformer circuit may include a plurality of cells configured in a matrix section and a unity matrix section wherein the unity matrix section cells represent the prediction of the remainder when the output of the multiplier circuit is a polynomial with a power less than the power of the irreducible polynomial.
Owner:ANALOG DEVICES INC
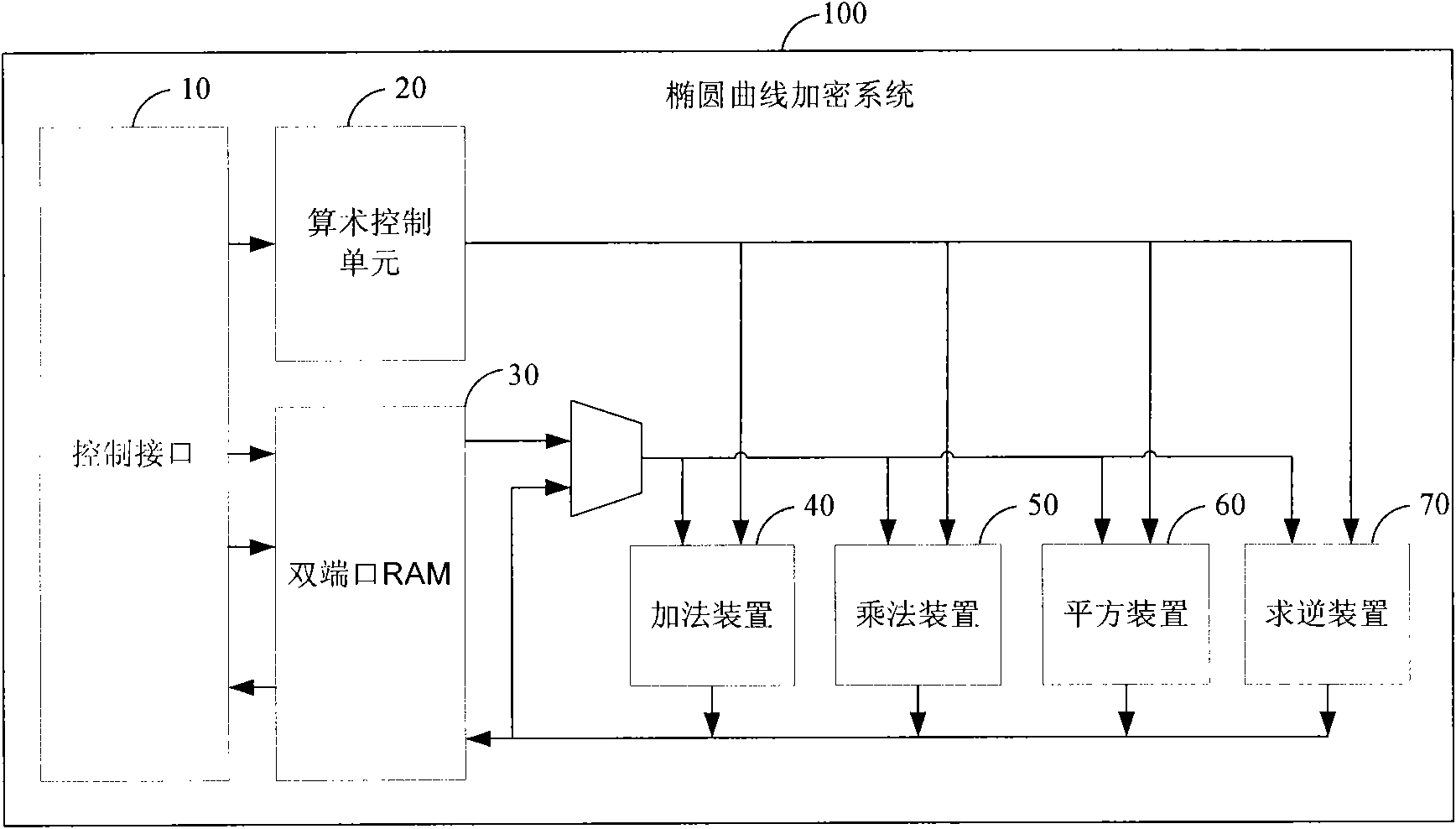
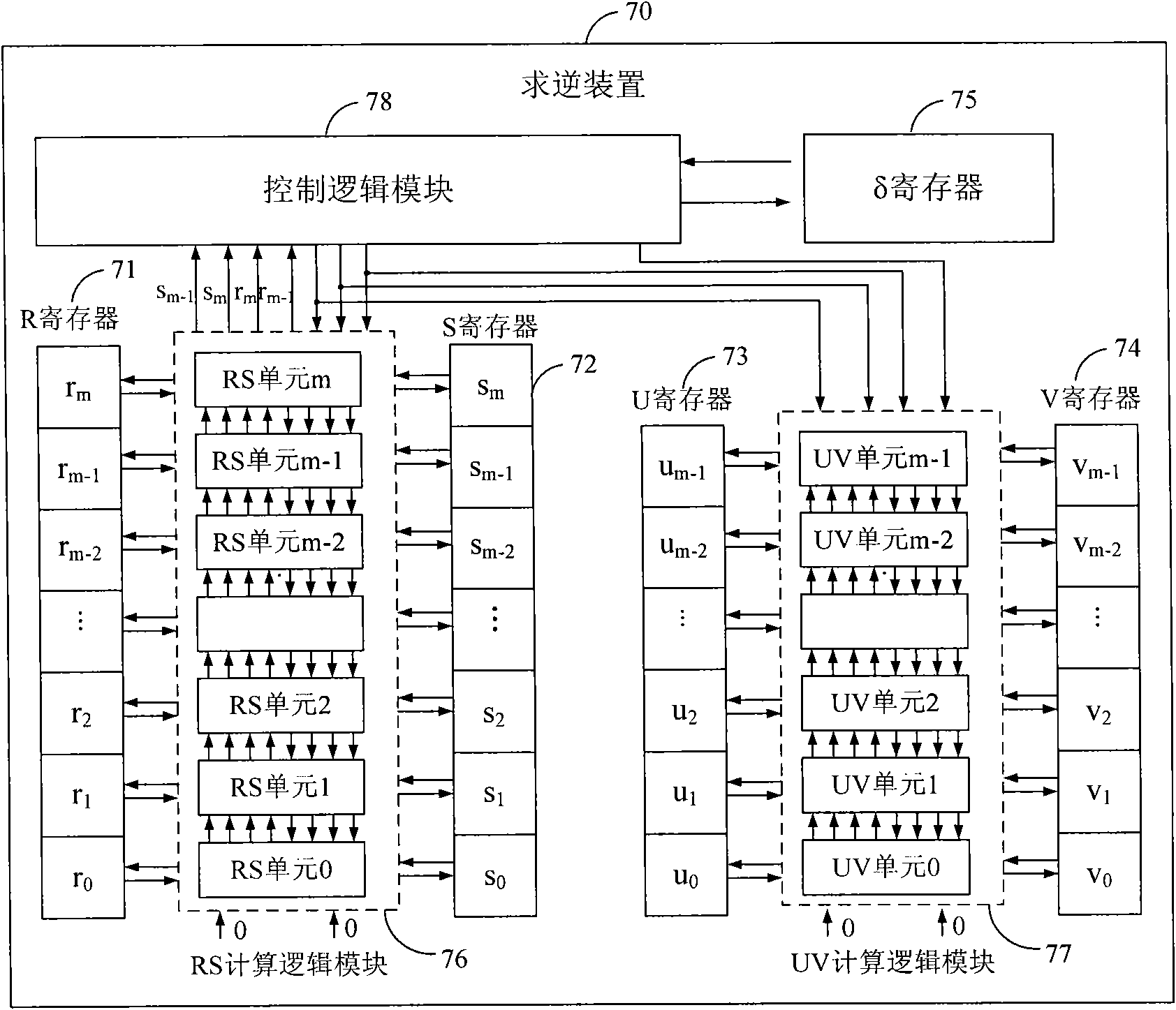
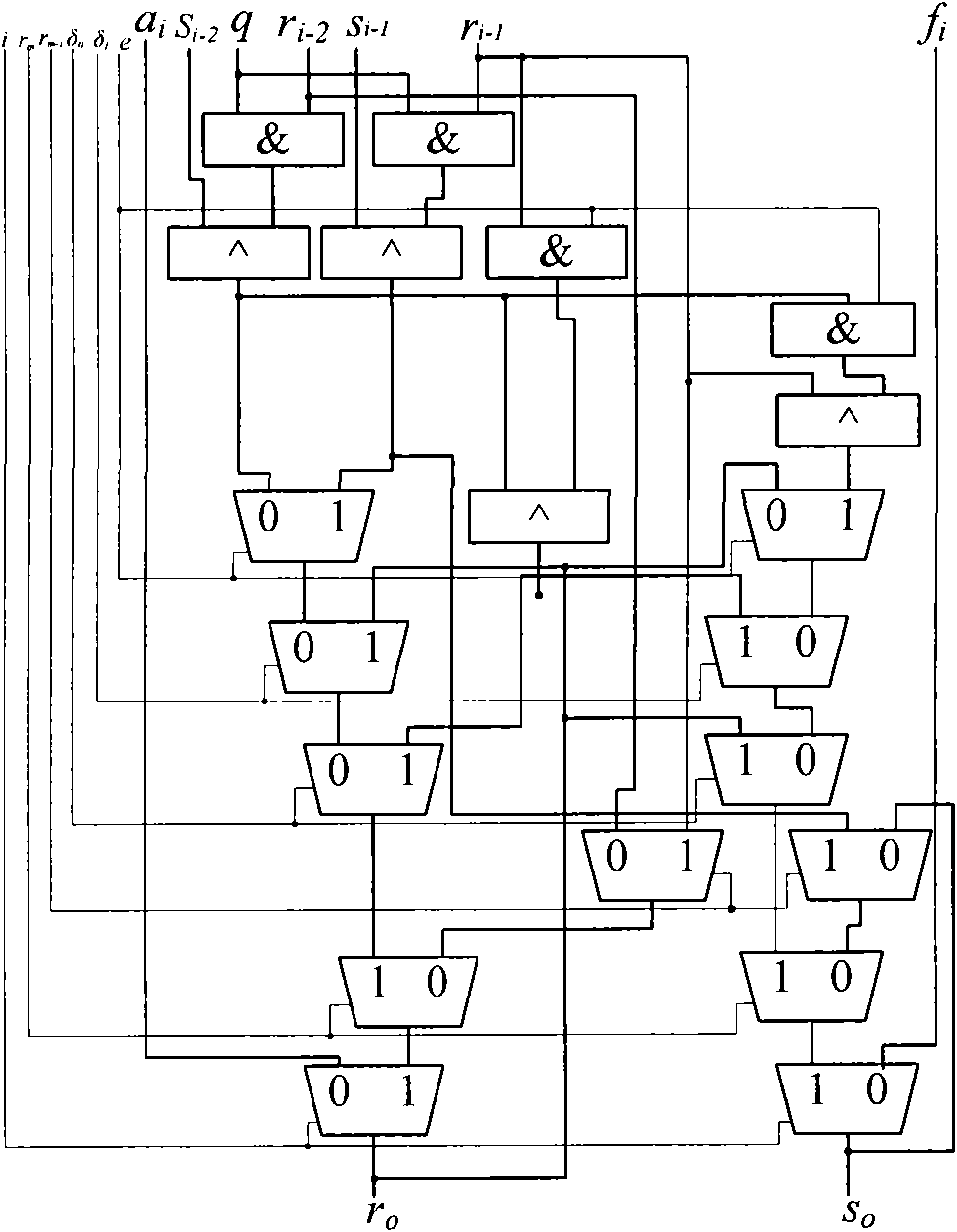
Finite field inversion method based on hardware design and device thereof
InactiveCN101572602ACalculation speedImprove the efficiency of inversion operationPublic key for secure communicationComputations using residue arithmeticResource utilizationComputer science
The invention discloses a finite field inversion method based on hardware design, which is applicable to an elliptical curve encrypt system. The method comprises the following steps: using a monadic polynomial in a finite field GF(p) as an input element a and defining an irreducible polynomial f(x), wherein a=am-1x+am-2x+to +a1x+a0, f(x)x=+fm-1xx+to +f(1)+f(0), ai and fi are respectively the coefficients of the input element a and the irreducible polynomial f(x); the input element a being repeatedly multiplied or divided by x and adding the results, and outputting the multiplicative inverse a of the input element a. Correspondingly, the invention further provides a finite field GF(2) inversion device based on the hardware design, therefore, the invention ensures rapider calculation speed, thereby greatly improving inversion operating efficiency. In addition, the working frequency of the inversion device is close to that of other operation devices in the encrypt system so as to fully improve the hardware source utilization rate of the inversion device.
Owner:陈婧 +3
Generic implementations of elliptic curve cryptography using partial reduction
ActiveUS7240084B2Digital computer detailsComputations using residue arithmeticDatapathComputer science
A reduction operation is utilized in an arithmetic operation on two binary polynomials X(t) and Y(t) over GF(2), where an irreducible polynomial Mm(t)=tm+am−1tm−1+am−2tm−2+ . . . +a1t+a0, where the coefficients ai are equal to either 1 or 0, and m is a field degree. The reduction operation includes partially reducing a result of the arithmetic operation on the two binary polynomials to produce a congruent polynomial of degree less than a chosen integer n, with m≦n. The partial reduction includes using a polynomial M′=(Mm(t)−tm)*tn−m, or a polynomial M″=Mm(t)*tn−m as part of reducing the result to the degree less than n and greater than or equal to m. The integer n can be the data path width of an arithmetic unit performing the arithmetic operation, a multiple of a digit size of a multiplier performing the arithmetic operation, a word size of a storage location, such as a register, or a maximum operand size of a functional unit in which the arithmetic operation is performed.
Owner:ORACLE INT CORP
Public key code hopping safety system and method
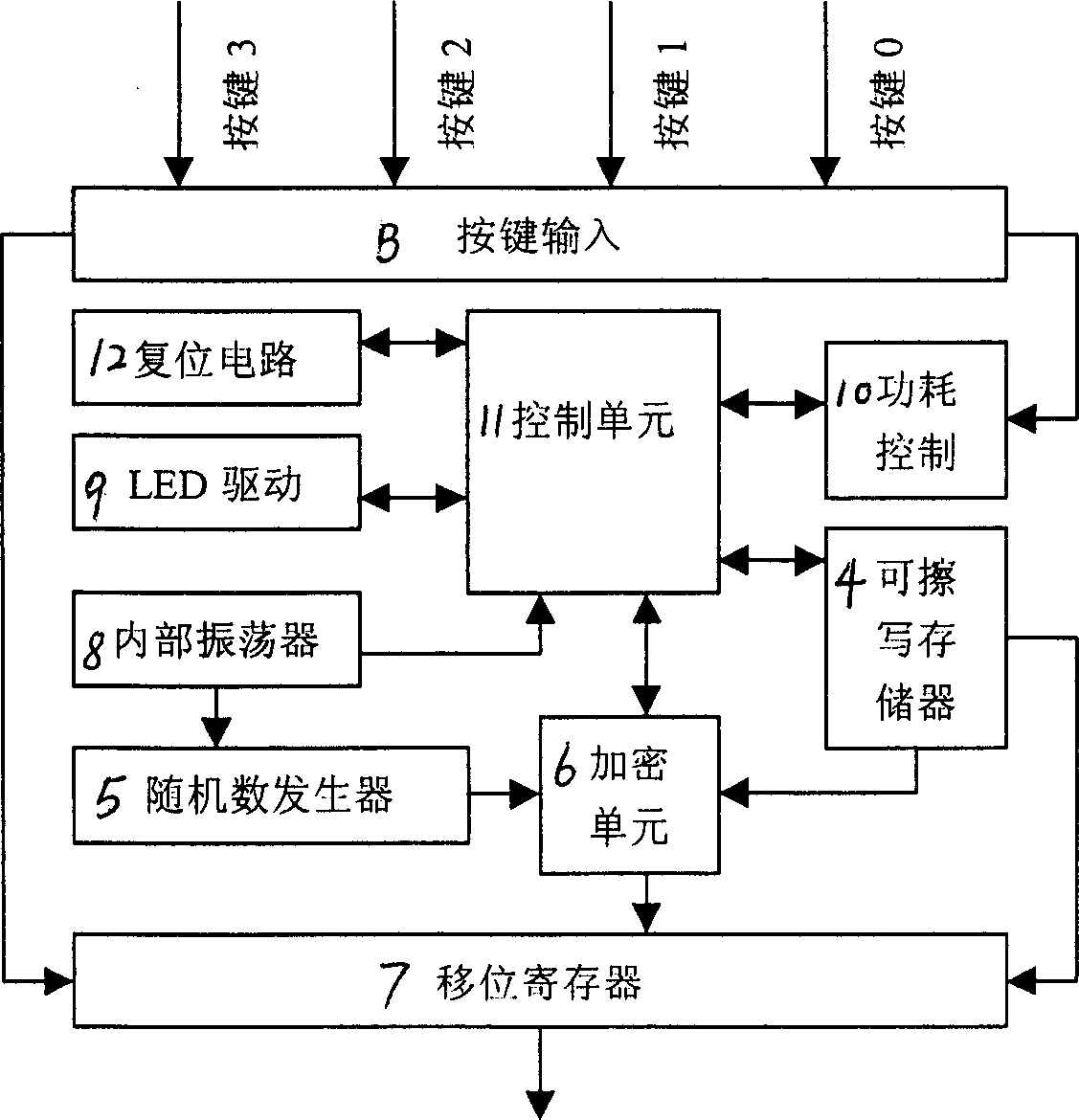
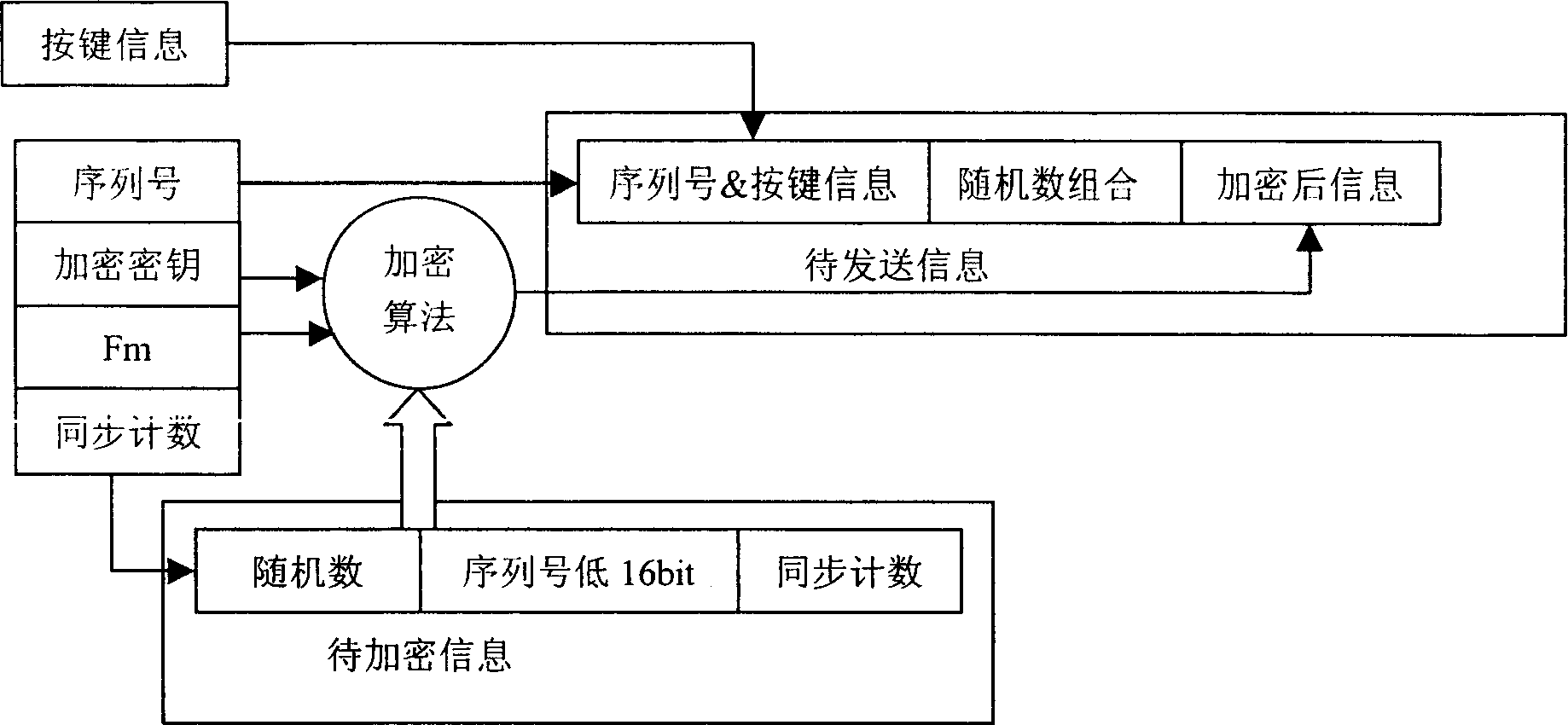
A public key code hopping safety system and method mainly includes electronic unlocking key transmitting end and receiving end. It features transmitting end received touch-tone signal controlling program to execute ciphering transmit operation, reading out product serial number, encryption key, synchronous counter value, and irreducible polynomial Fm value from memory, then loading these data into ciphering unit, after complete ciphering and loading to shift register to transmit, after receiving end received signal, controlling procedure reading in serial number, deciphering encryption key, irreducible polynomial, synchronizing enumeration data from memory, to make deciphering and verifying, writing back new synchronizing count value to memory, in executing training pattern, writing back new serial number and deciphering encryption key to memory, when serial number is effective but deciphering invalidation, effectively deciphering outputting alarm signal, successfully learning, writing in new serial number, synchronous counter value, and deciphering encryption key for refreshing memory. Said invention has advantage of high system safety and low cost.
Owner:贾松仁
Compound galois field engine and galois field divider and square root engine and method
InactiveUS20070271323A1Easy to reconfigureLess powerComputations using contact-making devicesDigital computer detailsEngineeringField element
A Galois field divider engine and method inputs a 1 and a first Galois field element to a Galois field reciprocal generator to obtain an output, multiplies in a Galois field reciprocal generator a first Galois field element by a first element of the Galois field reciprocal generator for predicting the modulo remainder of the square of the polynomial product of an irreducible polynomial m−2 times where m is the degree of the Galois field to obtain the reciprocal of the first Galois field element, and multiplying in the Galois field reciprocal engine the reciprocal of the first Galois field element by a second Galois field element for predicting the modulo remainder of the polynomial product for an irreducible polynomial to obtain the quotient of the two Galois field elements in m cycles; in a broader sense the invention includes a compound Galois field engine for performing a succession of Galois field linear transforms on a succession of polynomial inputs to obtain an ultimate output where each input except the first is the output of the previous Galois field linear transform; Galois field square root is achieved by inputting a Galois field element to a Galois field square root generator to obtain an output which is squared in the Galois field square root generator to predict the modulo remainder of the square of the polynomial product of an irreducible polynomial m−1 times where m is the degree of the Galois field to obtain the square root of the Galois field to obtain the square root of the Galois field element in (m−1) cycles.
Owner:ANALOG DEVICES INC
Encryption apparatus, decryption apparatus, and method
InactiveUS7773747B2Multiple keys/algorithms usagePublic key for secure communicationComputer hardwarePlaintext
A method whereby an encryption apparatus encrypts a message on the basis of a fibration X(x, y, t) serving as a public key when private keys are two or more sections corresponding to fibration X(x, y, t)=0 of an algebraic surface X, the method comprises embedding plaintext M obtained by concatenating the message to a random number as the coefficients of plaintext polynomial M(t) of degree l−1 or less, and generating encrypted text F=Epk(M, p, q, f, X) from the plaintext polynomial M(t) by an encrypting process of performing operations including at least one of addition, subtraction, and multiplication of random polynomials p(x, y, t), q(x, y, t), a random irreducible polynomial f(t) of degree l or more, and the fibration X(x, y, t) with respect to the plaintext polynomial M(t).
Owner:KK TOSHIBA
Generating cryptographic checksums
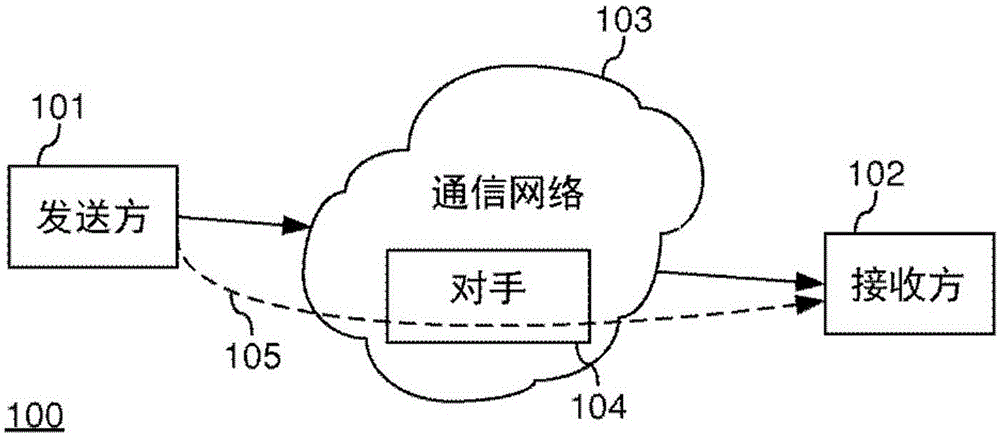
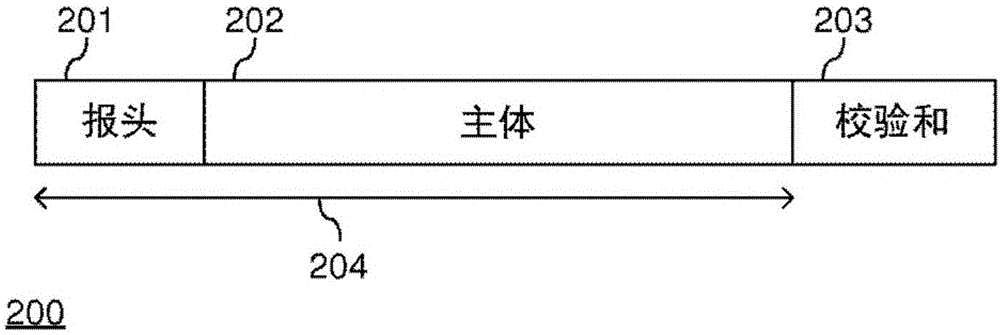
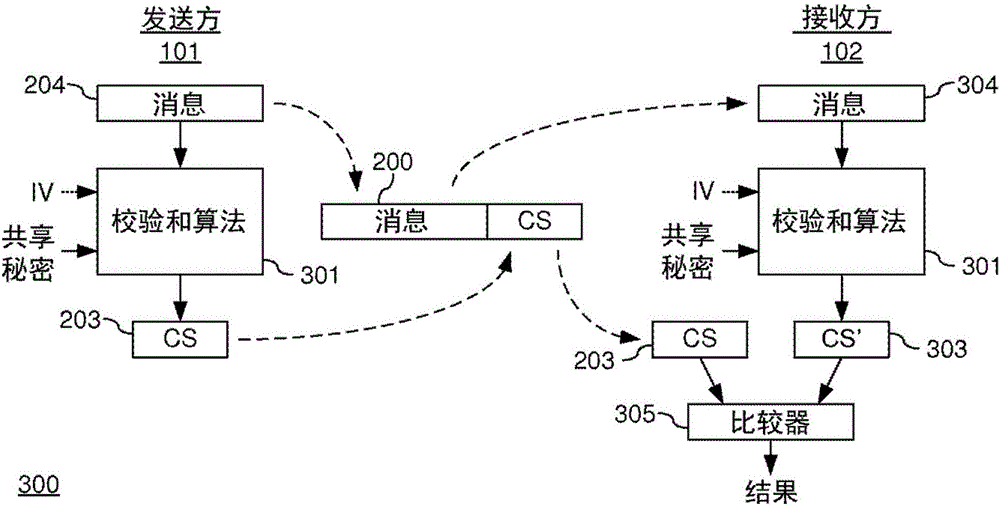
ActiveCN106688204ASave resourcesError preventionEncryption apparatus with shift registers/memoriesChecksumCryptographic nonce
A method (500) of generating a cryptographic checksum for a message M(x) is provided. The method comprises pseudo-randomly selecting (502) at least two irreducible polynomials p i (x). Each irreducible polynomial p i (x) is selected based on a first cryptographic key from the set of irreducible polynomials of degree ni over a Galois Field. The method further comprises calculating (503) a generator polynomial p(x) of degree n = formula (I) as a product of the N irreducible polynomials formula (II), and calculating (505) the cryptographic checksum as a first function g of a division of a second function of M(x), (M(x)), modulo p(x), i.e., g( (M(x)) mod p(x)). By replacing a standard checksum, such as a Cyclic Redundancy Check (CRC), with a cryptographic checksum, an efficient message authentication is provided. The proposed cryptographic checksum may be used for providing integrity assurance on the message, i.e., for detecting random and intentional message changes, with a known level of security. Further, a corresponding computer program, a corresponding computer program product, and a checksum generator for generating a cryptographic checksum, are provided.
Owner:TELEFON AB LM ERICSSON (PUBL)
Construction method of two-dimensional optical address codes suitable for visible light OCDMA (Optical Code Division Multiple Access) communication
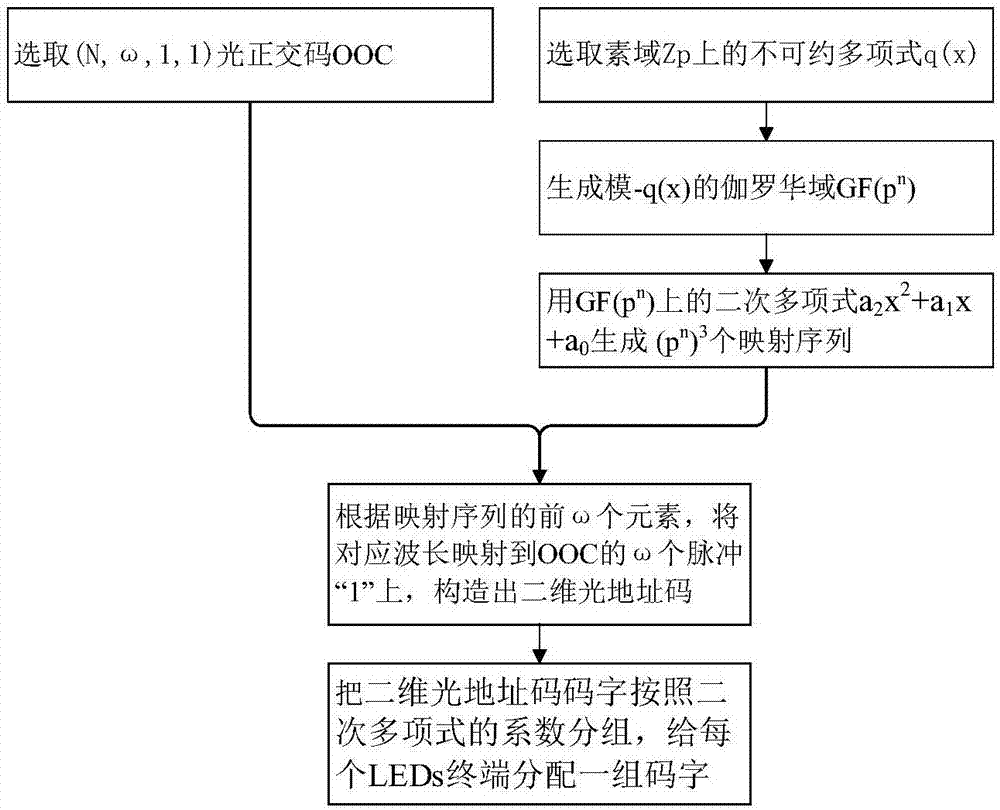
ActiveCN106911384AIncrease freedomChoice does not affectWavelength-division multiplex systemsClose-range type systemsMulti user interferenceLength wave
The invention provides a construction method of two-dimensional optical address codes suitable for visible light OCDMA (Optical Code Division Multiple Access) communication, and aims to solve the technical problems of limitation on wave number selection and difficulty in gaining both a large code set and a low cross-correlation value in the prior art. The method comprises the following implementation steps: generating a galois field according to an irreducible polynomial on a prime field; generating a mapping sequence according to a quadratic polynomial on the galois field; mapping a corresponding wavelength onto pulses of one-dimensional optical address codes according to the mapping sequence to obtain two-dimensional optical address codes; and grouping the two-dimensional optical address codes, and allocating a group of code words to each LEDs (Light Emitting Diodes) communication terminal in the visible light communication. In the construction method, the mapping sequence is generated through the quadratic polynomial on the galois field, so that selection of a two-dimensional optical address code wave number is more flexible. Moreover, the two-dimensional optical address codes are grouped, so that a visible light communication network can accommodate more users, and multi-user interference under the coverage of the same LEDs illuminating communication terminal is restrained.
Owner:XIDIAN UNIV
Quantum digital signature and quantum digital signcryption method
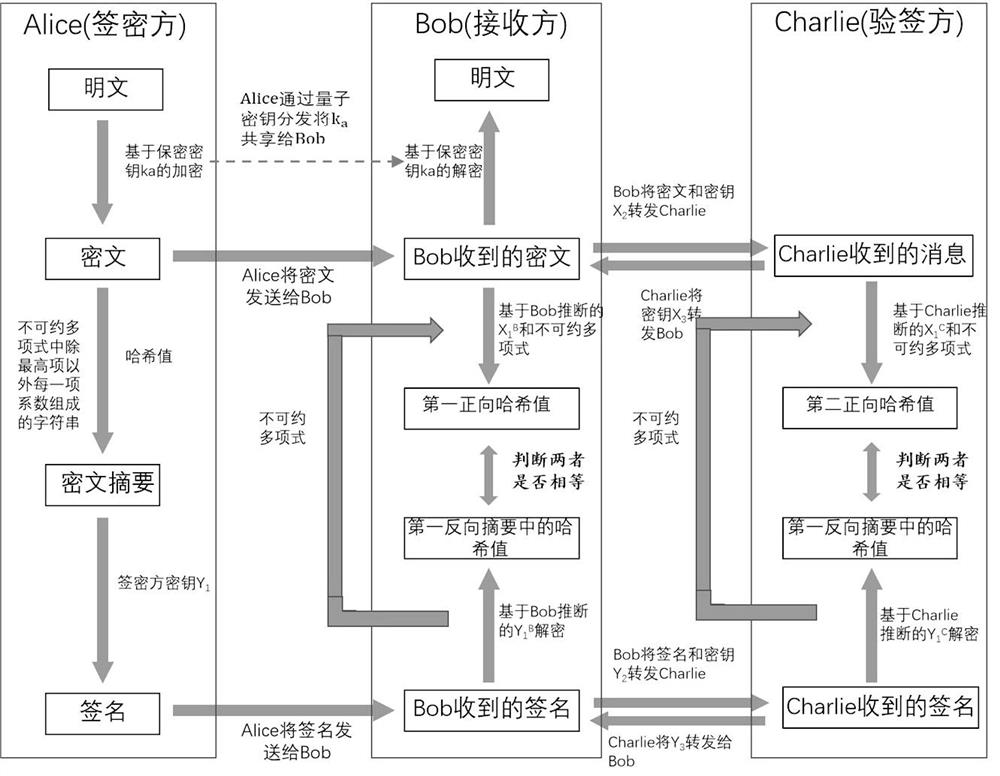
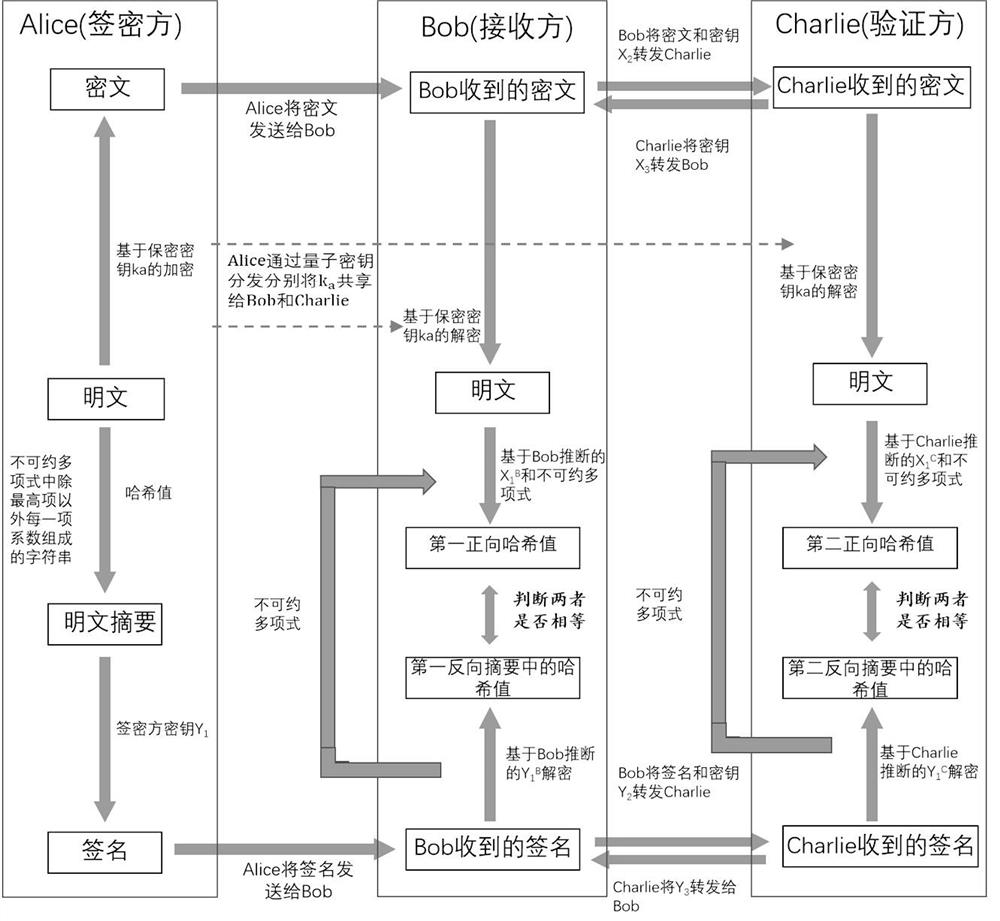
ActiveCN113779645AUnconditionally Secure SigncryptionSecure signcryptionQuantum computersDigital data protectionHash functionAlgorithm
The invention discloses a quantum digital signature and a quantum digital signcryption method. The quantum digital signature comprises the following steps: generating a secret key; generating a digital signature; and verifying the digital signature. The security of the hash function used in the signcryption or signature process is ensured by the irreducible polynomial and the hash function key serving as the input random number, and the irreducible polynomial depends on the local random number and cannot be known by a receiver and a signature verification party in advance before the signcryption or signature process; in other words, the unconditionally secure hash function is used so that the security of the whole signcryption or signature process is ensured, and the security risk caused by leakage of a fixed irreducible polynomial in other signatures is directly avoided; and moreover, the length of the message is not limited when the hash value is generated, the message with any length can be signed or signcrypted in each round of signature or signcryption, and the signature or signcryption efficiency is very high.
Owner:NANJING UNIV +1
Compact galois field multiplier enginer
InactiveCN1717671AComputation using non-contact making devicesDigital computer detailsTransformerIrreducible polynomial
A compact Galois field parallel multiplier engine includes a multiplier circuit for multiplying together two polynomials with coefficients over a Galois field to obtain their product; a Galois field linear transformer circuit has a multiply input from the multiplier circuit for predicting the modulo remainder of the polynomial product for an irreducible polynomial; first and second polynomial inputs; the Galois field linear transformer circuit may include a plurality of cells configured in a matrix section and a unity matrix section wherein the unity matrix section cells represent the prediction of the remainder when the output of the multiplier circuit is a polynomial with a power less than the power of the irreducible polynomial.
Owner:ANALOG DEVICES INC
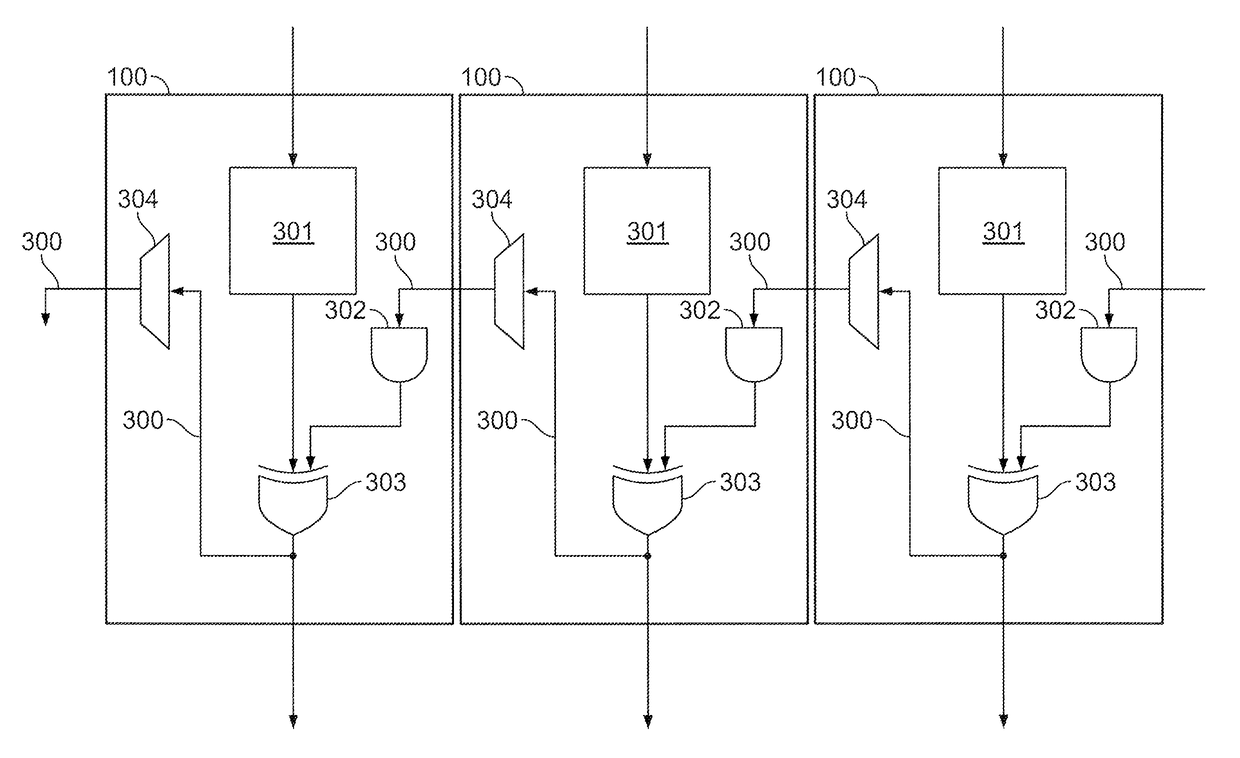
Circuitry and methods for implementing Galois-field reduction
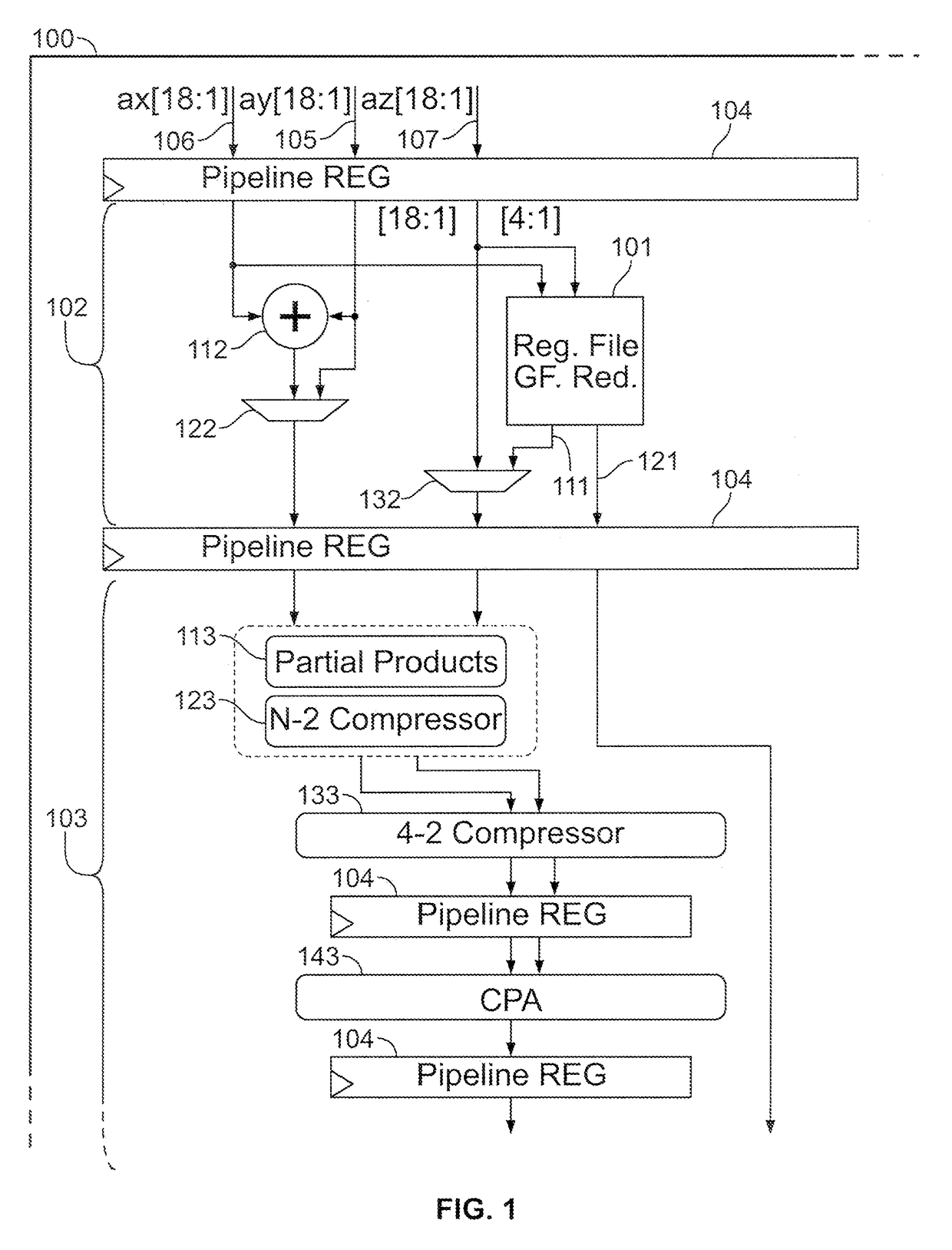
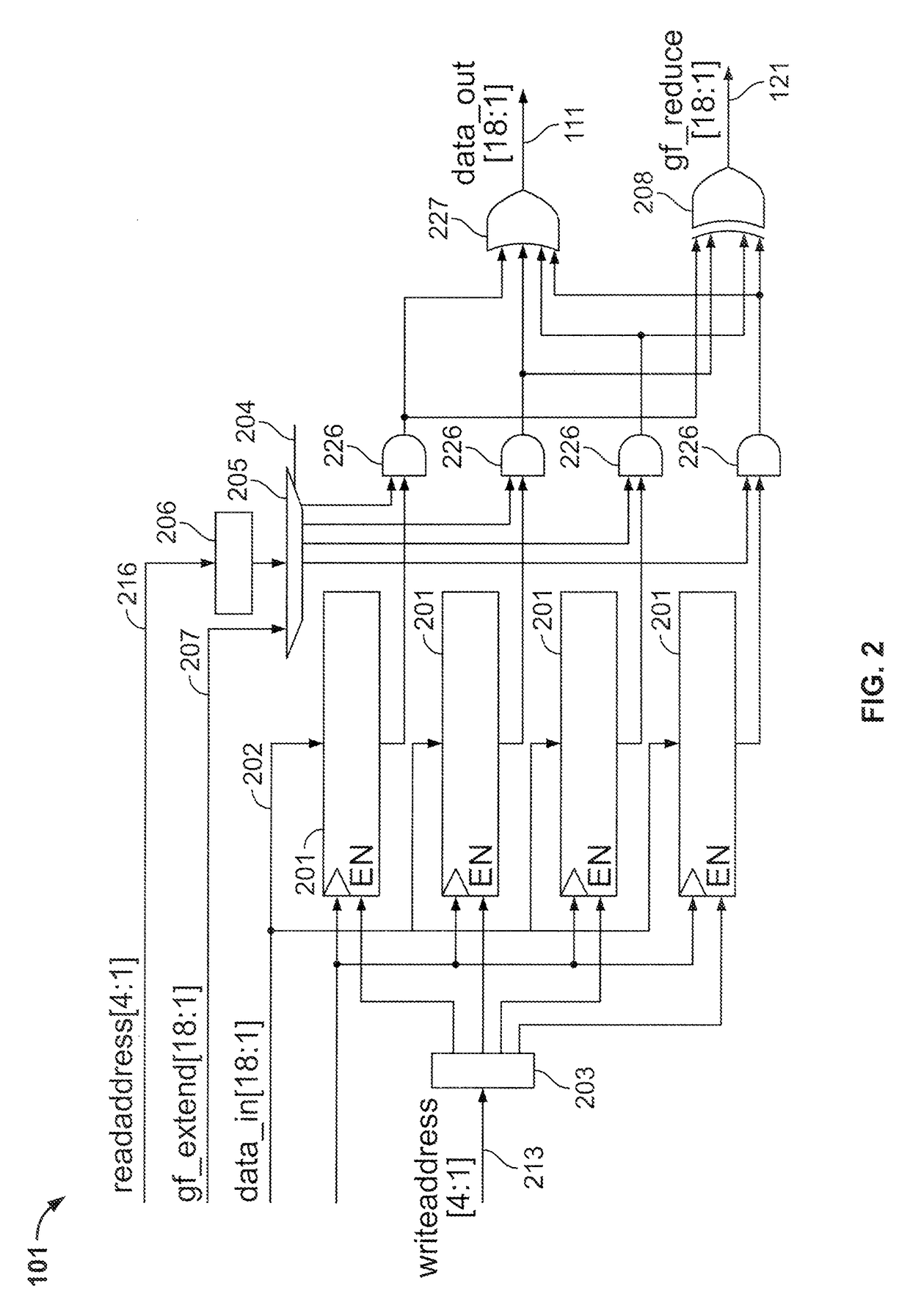
ActiveUS9619207B1Facilitate Galois-field reduction operationReduce stepsComputations using residue arithmeticBinary multiplierComputer architecture
Galois-field reduction circuitry for reducing a Galois-field expansion value using an irreducible polynomial includes a plurality of memories, each for storing a respective value derived from the irreducible polynomial and a respective expansion bit position. Gates select ones of said the plurality of memories corresponding to ones of the respective expansion bit positions that contain ‘1’, and an exclusive-OR gate combines outputs of the gates that select. A specialized processing block includes a multiplier stage, and an input stage upstream of the multiplier stage, with such Galois-field reduction circuitry in the input stage with its output selectably connectable to the multiplier stage and selectably connectable to an output of the specialized processing block. A programmable integrated circuit device includes a plurality of such specialized processing blocks, and additional multiplier and additional exclusive OR gates for concatenating a plurality of specialized processing blocks.
Owner:ALTERA CORP
Serial finite field multiplier
ActiveUS6917218B2Computation using non-contact making devicesDigital computer detailsArray data structureTheoretical computer science
The present invention relates to a finite field multiplier used for implementing an encrypting algorithm circuit, thereby minimizing power consumption and circuit area in implementing the finite field multiplier with a LFSR (Linear Feedback Shift Register) structure. The Finite field multiplier of the present invention is an operator performing a modular operation on the multiplication result of two data represented on a polynomial basis in a Galois Field into an irreducible polynomial. The LFSR structure is a serial finite field multiplication structure, and has a merit over an array structure and a hybrid structure in application to systems that are limited in size and power due to its simplicity of circuits and also its capability of being implemented in a small size.
Owner:ELECTRONICS & TELECOMM RES INST
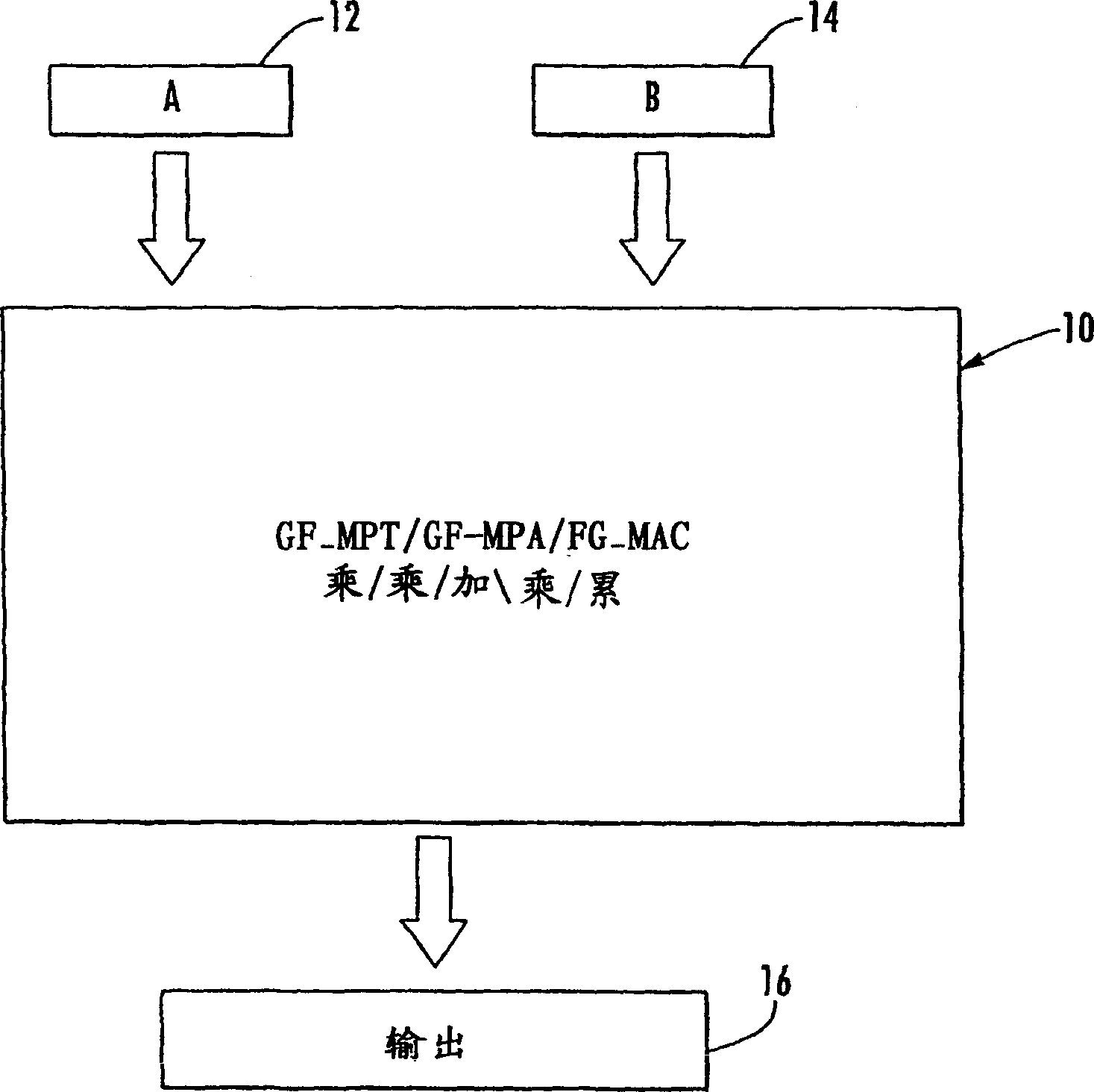
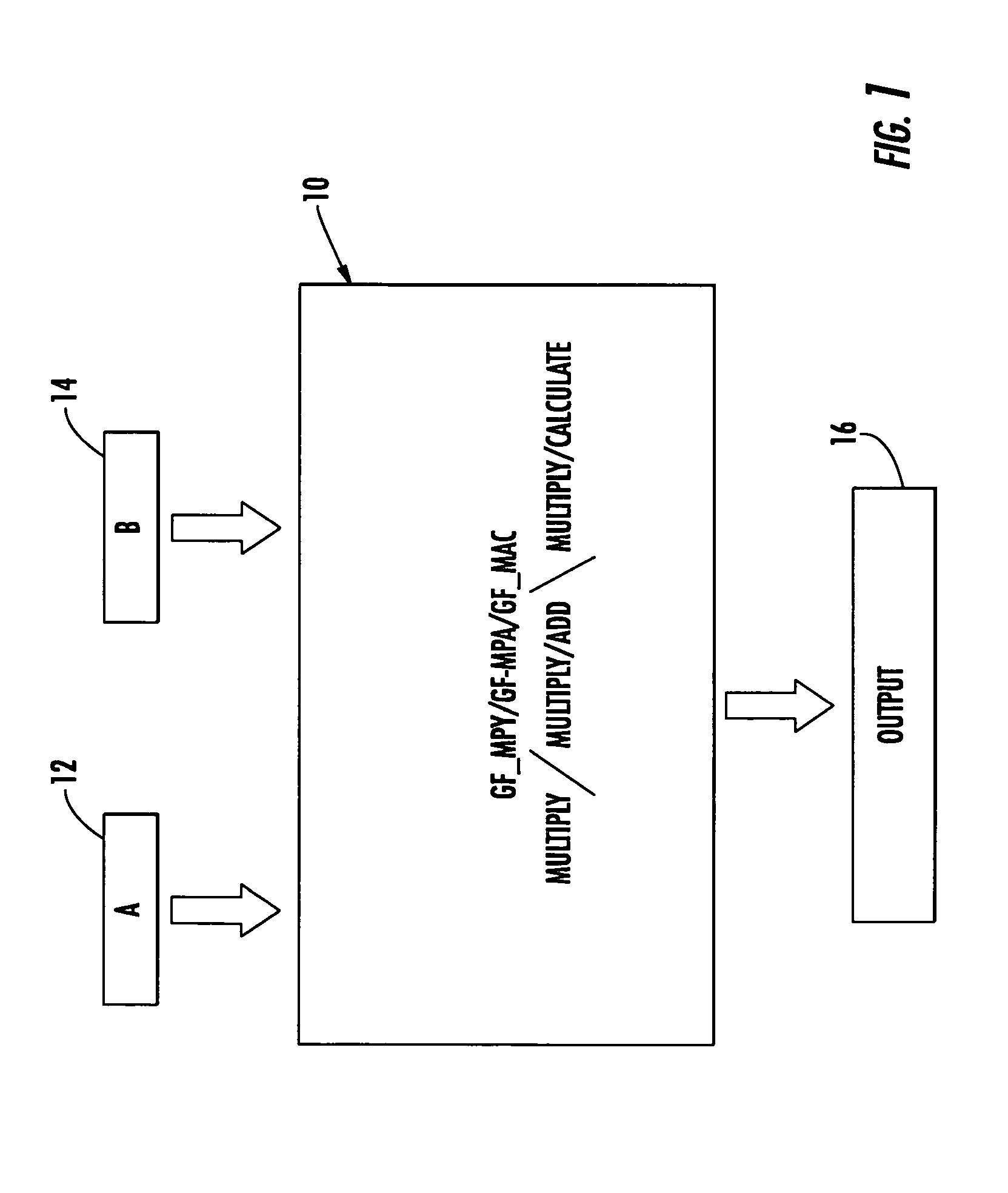
Galois field multiply/ multiply-add/multiply accumulate
InactiveCN1608244AImprove performanceCodes simulation/testingComputations using residue arithmeticBinary multiplierTransformer
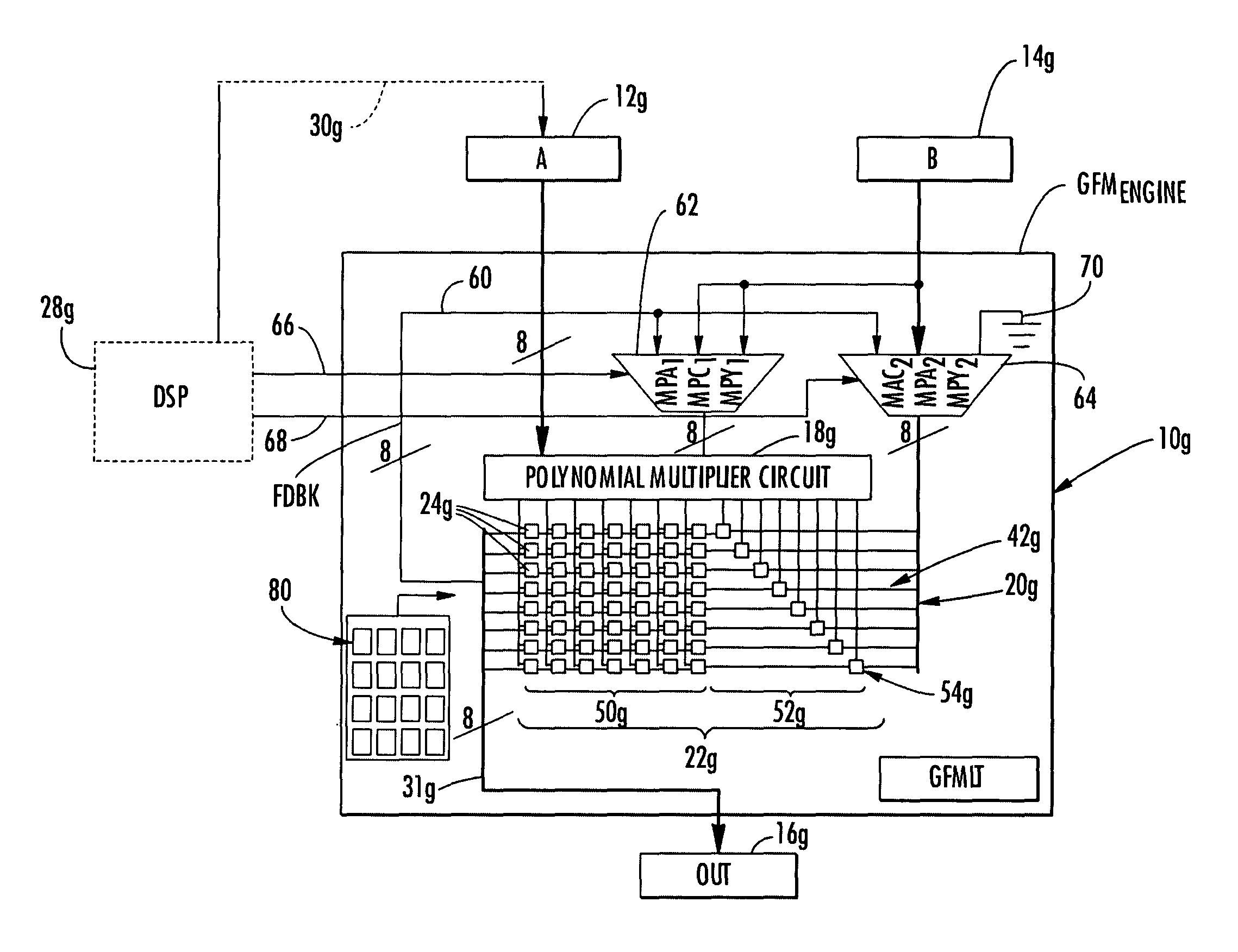
A Galois field multiply / multiply-add / multiply-accumulate system includes a multiplier circuit for multiplying two polynomials with coefficients over a Galois field to obtain their product; a Galois field linear transformer circuit responsive to the multiplier circuit for predicting the modulo remainder of the polynomial product for an irreducible polynomial; a storage circuit for supplying to the Galois field linear transformer circuit a set of coefficient for predicting the modulo remainder for a predetermined irreducible polynomial; and a Galois field adder circuit for adding the product of the multiplier circuit with a third polynomial with coefficients over a Galois field for performing the multiplication and add operations in a single cycle.
Owner:ANALOG DEVICES INC
Compound Galois field engine and Galois field divider and square root engine and method
InactiveUS7895253B2Easy to reconfigureReduce areaComputations using contact-making devicesDigital computer detailsEngineeringField element
A Galois field divider engine and method inputs a 1 and a first Galois field element to a Galois field reciprocal generator to obtain an output, multiplies in the Galois field reciprocal generator the first Galois field element by the output of the Galois field reciprocal generator for predicting the modulo remainder of the square of the polynomial product of an irreducible polynomial m−2 times to obtain the reciprocal of the first Galois field element, and multiplies the reciprocal element by a second Galois field element for predicting the quotient of the two Galois field elements in m cycles; in a broader sense the invention includes a compound Galois field engine for performing a succession of Galois field linear transforms on a succession of polynomial inputs to obtain an ultimate output where each input except the first is the output of the previous Galois field linear transform.
Owner:ANALOG DEVICES INC
Techniques for performing reduced complexity galois field arithmetic for correcting errors
Techniques are provided for performing Galois field arithmetic to detect errors in digital data stored on disks. Two 12-bit numbers or two 10-bit numbers are multiplied together in Galois field using tower arithmetic. In the 12-bit embodiment, a base field GF(2) is first extended to GF(23), GF(23) is extended to a first quadratic extension GF(26), and GF(26) is extended to a second quadratic extension GF(212). In the 10-bit embodiment, the base field GF(2) is first extended to GF(25), and GF(25) is extended to a quadratic extension GF(210). Each of the extensions for the 10-bit and 12-bit embodiments is performed using an irreducible polynomial. All of the polynomials used to generate the first and the second quadratic extensions of the Galois field are in the form x2+x+K, where K is an element of the ground field whose absolute trace equals 1.
Owner:WESTERN DIGITAL TECH INC
Programmable error correction capability for BCH codes
An embodiment of the invention relates to a BCH encoder formed with linear feedback shift registers (LFSRs) to form quotients and products of input polynomials with irreducible polynomials of a generator polynomial g(x) of the BCH encoder, with and without pre-multiplication by a factor xm. The BCH encoder includes multiplexers that couple LFSR inputs and outputs to other LFSRs depending on a data input or parity generation state. The BCH encoder can correct up to a selectable maximum number of errors in the input polynomials. The BCH encoder further includes LFSR output polynomial exponentiation processes to produce partial syndromes for the input data in a syndrome generation state. In the syndrome generation state the LFSRs perform polynomial division without pre-multiplication by the factor xm. The exponentiation processes produce partial syndromes from the resulting remainder polynomials of the input data block.
Owner:INFINEON TECH AG
Byte substitution method applied to AES algorithm and system thereof
ActiveCN105577362ASave logic resourcesIncrease working frequencyEncryption apparatus with shift registers/memoriesExtended Euclidean algorithmDatapath
The invention relates to a byte substitution method applied to an AES algorithm, characterized by comprising the following steps of: expressing each byte of input data of an internal data path of the AES algorithm as one element in a finite field GF (28), calculating a multiplicative inverse of the input data in the finite field GF (28) based on an irreducible polynomial through an extended Euclidean algorithm, and then performing affine arithmetic for the obtained multiplicative inverse to obtain a byte substitution result. The substitution method provided by the invention solves the multiplicative inverse through the extended Euclidean algorithm, and then realizes a byte substitution function in the AES algorithm through performing the extended Euclidean algorithm for the multiplicative inverse, thus, compared with the prior art, the method can save logic resource maximally, and can effectively improve working efficiency of the system.
Owner:SYSU HUADU IND SCI & TECH INST
Method, apparatus, and computer program product for determining data signatures in a dynamic distributed device network
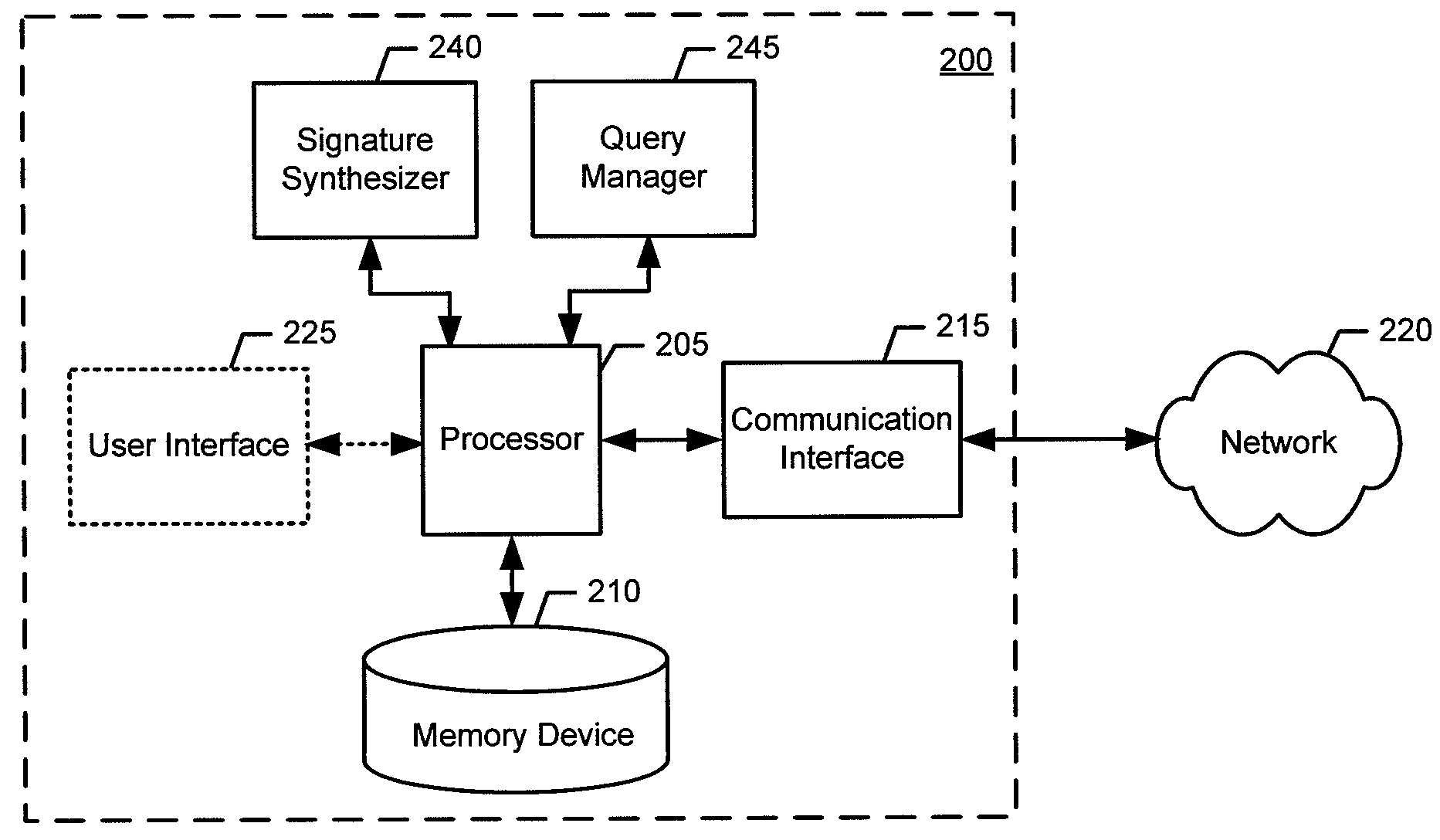
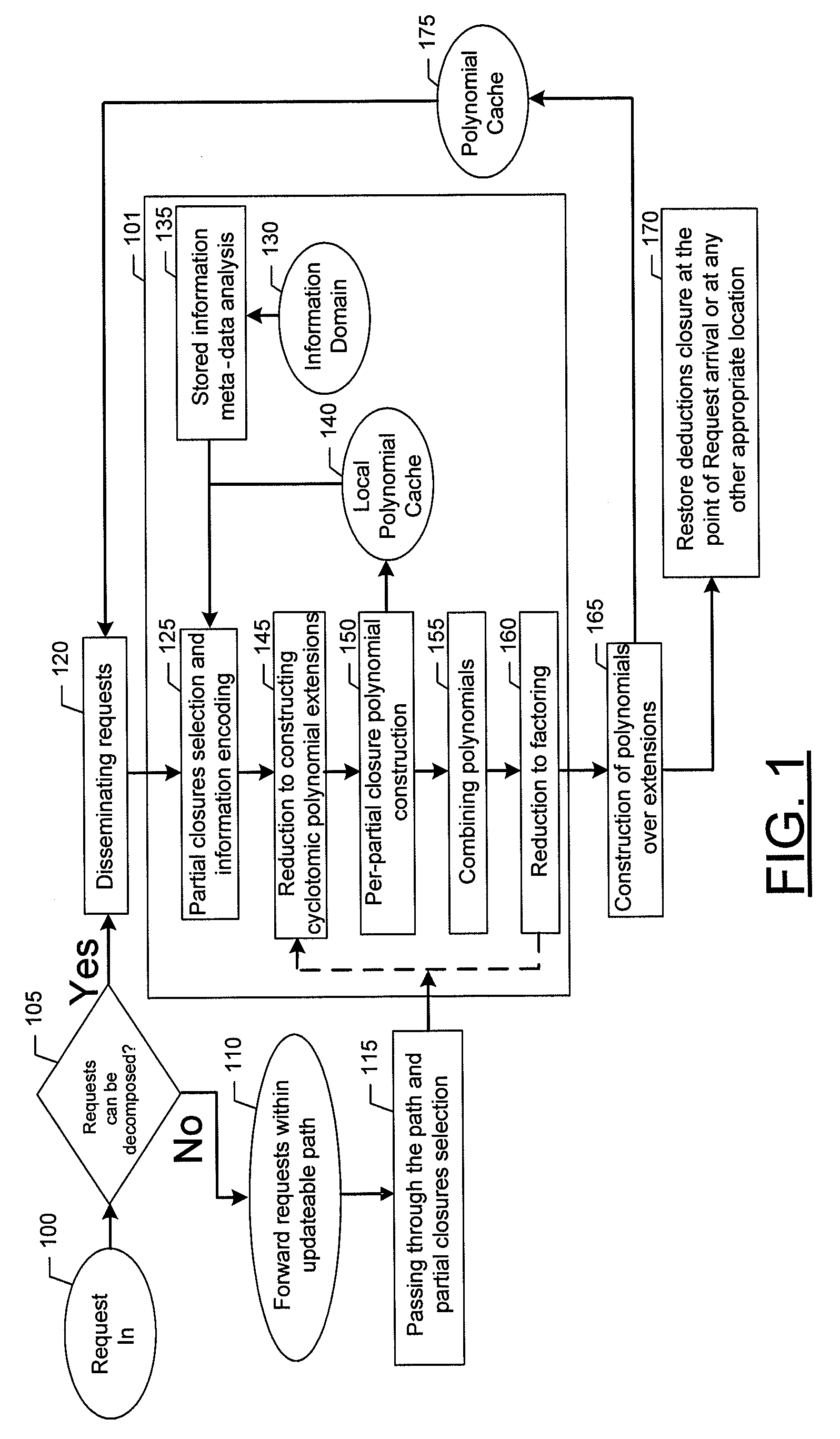
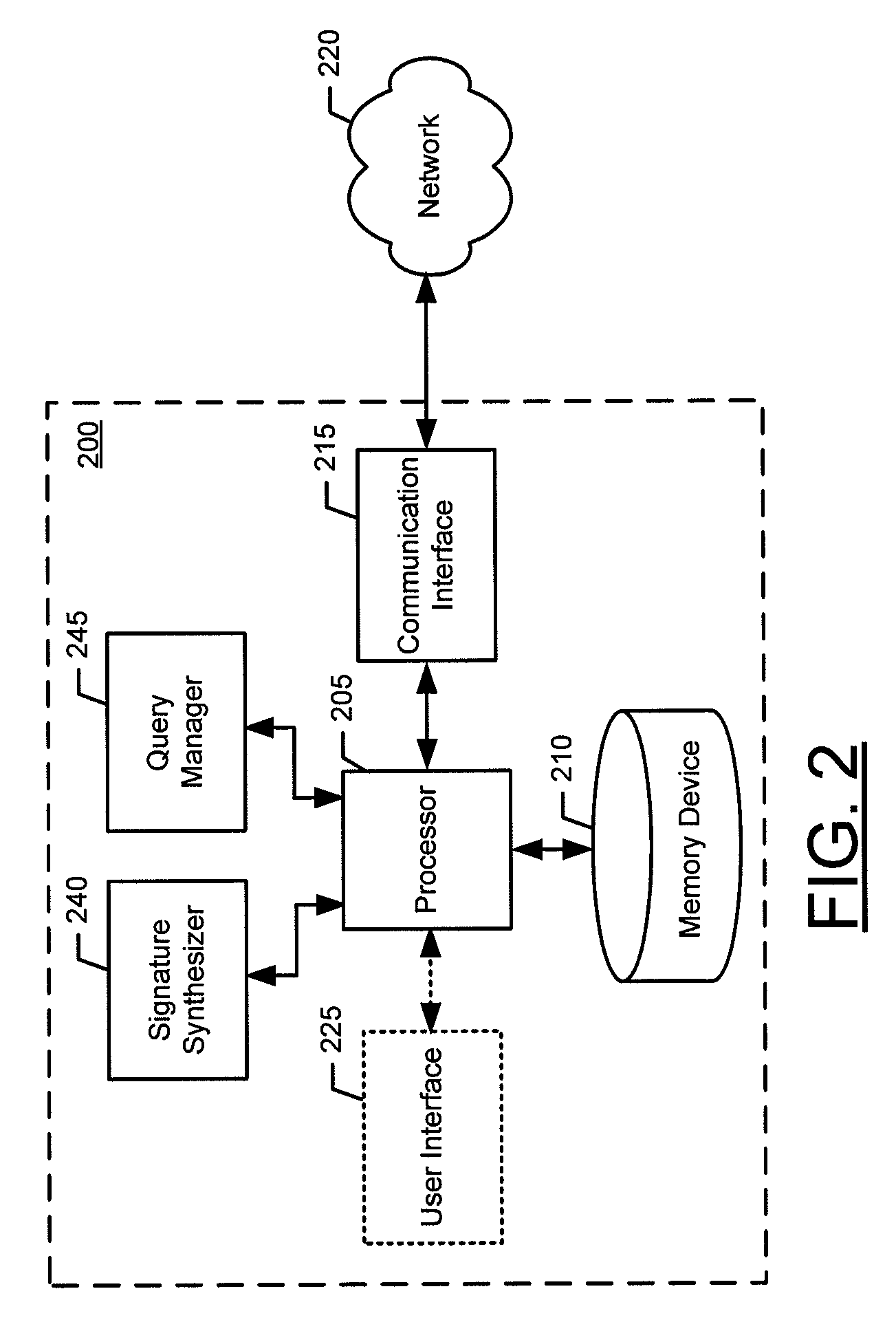
InactiveUS20100169345A1Reduce the burden onImprove balanceDigital data processing detailsDatabase distribution/replicationPartial closureData mining
An apparatus for determining data signatures in a dynamic distributed device network may include a processor. The processor may be configured to receive a first query and generate a local partial closure of the data identified by the first query. The processor may be further configured to synthesize a data signature of the local partial closure. In this regard, the data signature may be an irreducible polynomial expression and the data signature may be orthogonal to remote data signatures generated from remote partial closures. Further, the processor may be configured to store the data signature in an information store within a dynamic distributed device network. Associated methods and computer program products may also be provided.
Owner:PIECE FUTURE PTE LTD
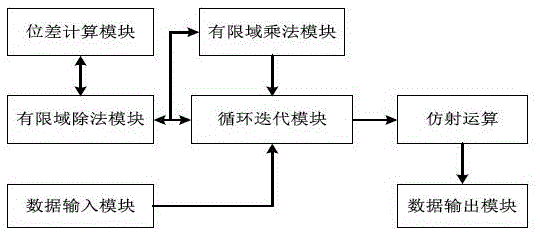
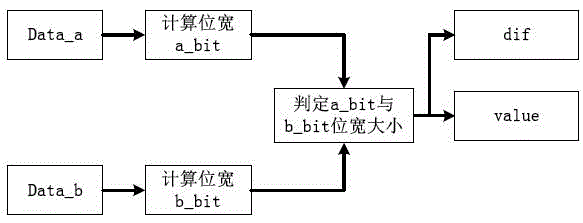
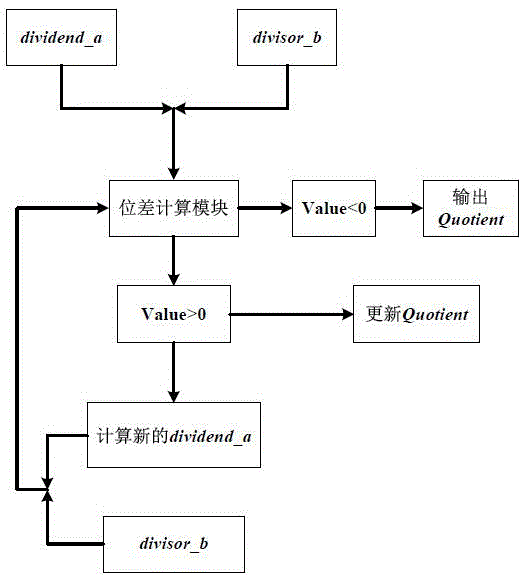
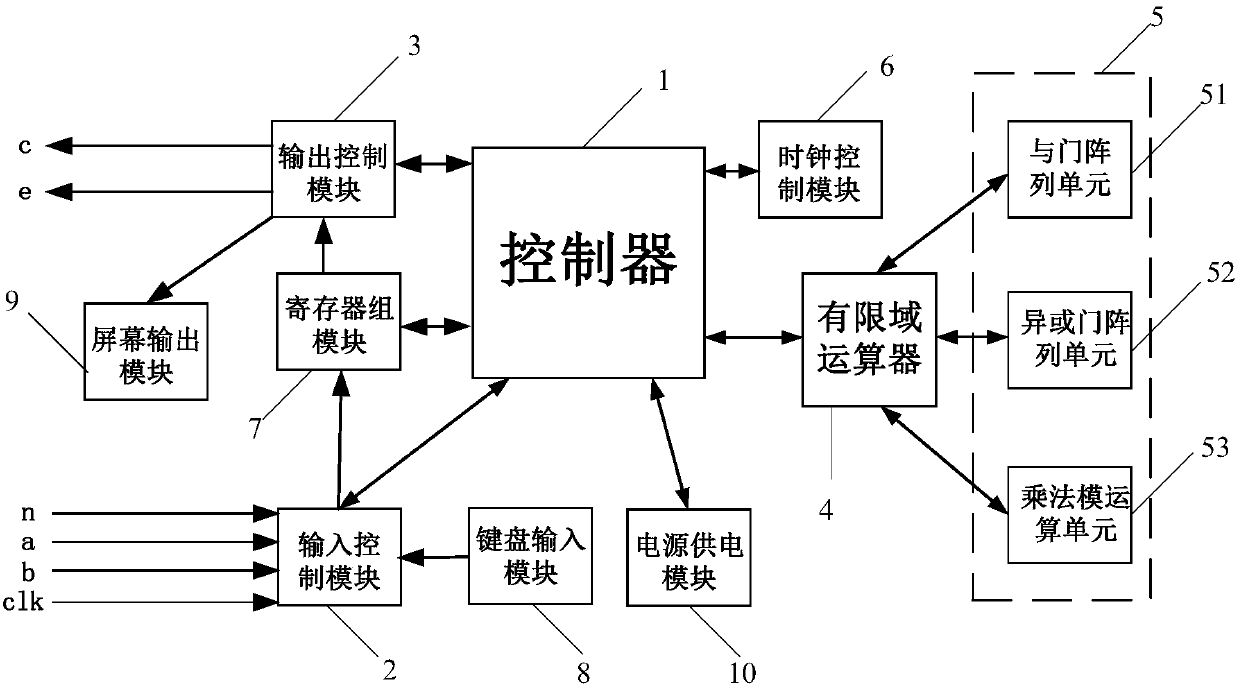
All-in-one irreducible polynomial based finite field multiplier
The invention relates to an all-in-one irreducible polynomial based finite field multiplier which comprises a controller, an input control module, an output control module, a finite field multiplier and an operation module, wherein the controller is used for controlling and scheduling data transmission among the input control module, the output control module and the finite field multiplier; the input control module is used for inputting a multiplication operation number a(x) and a multiplication operation number b(x) when detecting that a finite field GF(2n) has an all-in-one irreducible polynomial; the finite field multiplier is used for calling the operation module to carry out finite field multiplication operation on the multiplication operation number a(x) and the multiplication operation number b(x) to obtain a multiplication operation result c(x); the operation module is used for implementing and logical operation, exclusive or logic operation and modular operation; the output control module is used for outing the multiplication operation result c(x). By adopting the multiplier, the operation efficiency of finite field multiplication is improved.
Owner:SHENZHEN POLYTECHNIC
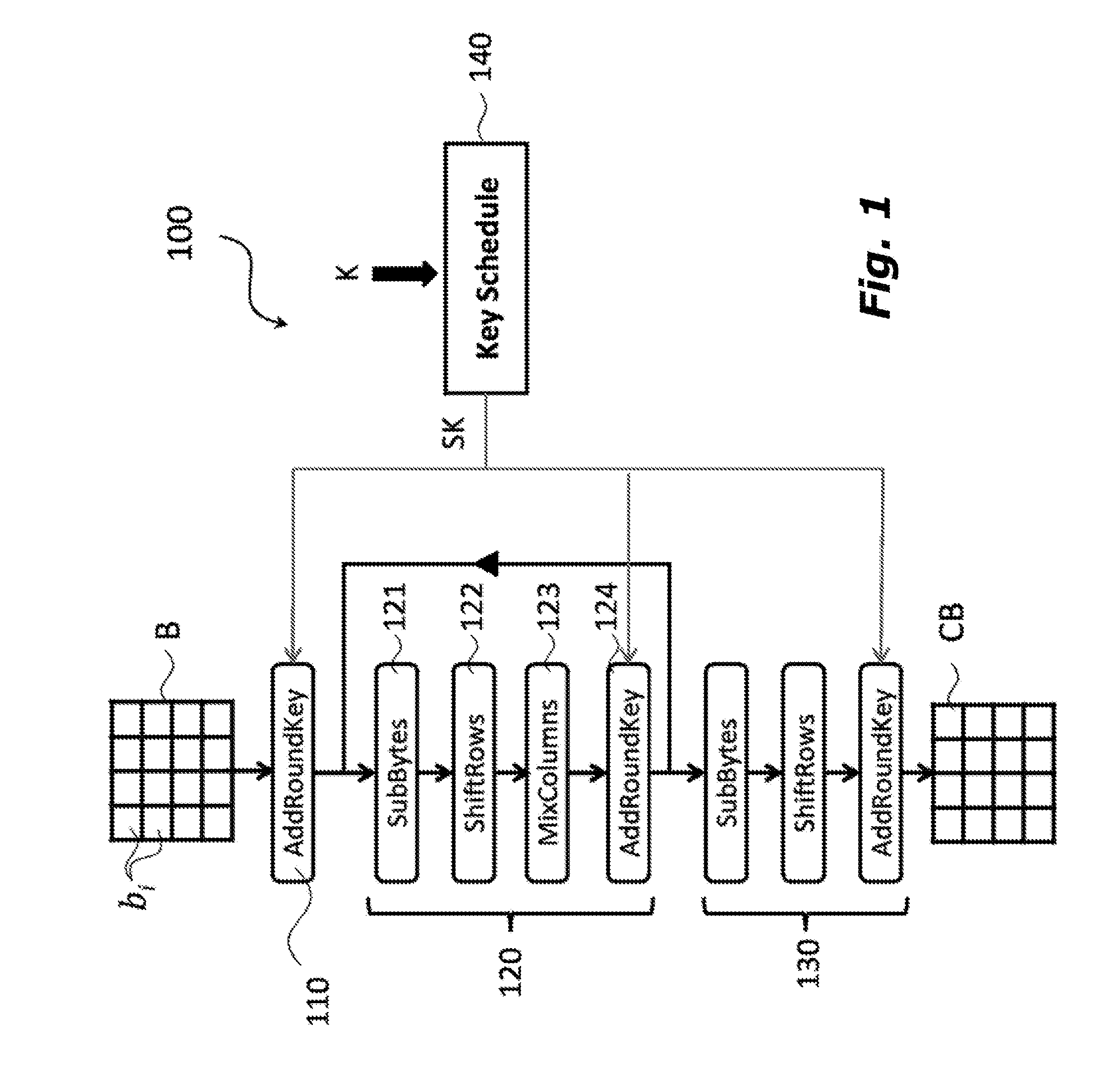
Method for performing an encryption of an AES type, and corresponding system and computer program product
ActiveUS9425961B2Improve securityMultiple keys/algorithms usageEncryption apparatus with shift registers/memoriesChinese remainder theoremTheoretical computer science
A polynomial representation (bi(x)) in an AES finite field(Z2[x](r(x)))of input bytes (bi) of a state matrix (B) is obtained. A plurality (1) of irreducible polynomials (fi(y)) and a moving map (ψi) are used to map each polynomial (bi(x)) of the polynomial representation into a respective field of polynomials(Z2[y](fi(y)))computed with respect to one of the irreducible polynomials (fi(y)), to obtain respective moved polynomials (αi(y)). The moved polynomials (αi(y)) are mapped into a polynomial (a(z)) of a polynomial ring(Z2[z](p(z))),obtained by applying an isomorphism (ω) between the fields of polynomials(Z2[y](fi(y)))and the polynomial ring(Z2[z](p(z)))based upon the Chinese remainder theorem (CRT). AES encryption is applied to the polynomial (a(z)). The polynomial (a(z)) is reconverted into the AES finite field(Z2[x](r(x)))to obtain an encrypted state matrix (CB).
Owner:STMICROELECTRONICS SRL
Features
- R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
Why Patsnap Eureka
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com