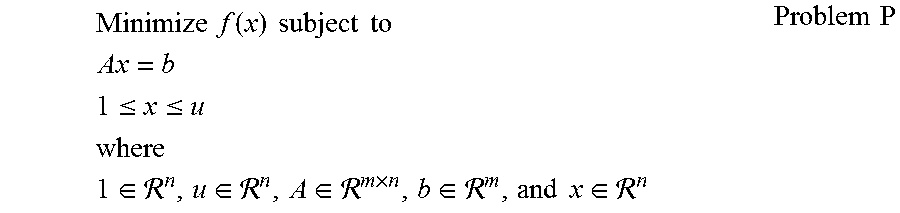Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Flexible vector-processing algorithms for numerically solving extreme-scale, linear and non-linear, predictive and prescriptive, problems in science and engineering, on parallel-processing super computers

a technology of supercomputers and vector processing algorithms, applied in the field of new vector parallelprocessing algorithms for numerically solving extreme-scale scientific and engineering problems, can solve the problems of insufficient scope and complexity of commercial electrical power distribution networks, limited utility of existing geometric programming techniques, and inability to solve extreme-scale (sometimes referred to as exa-scale or mult-scale) problems involving millions and even billions of decision variables

Inactive Publication Date: 2017-01-26
PETERSON ELMOR L
View PDF0 Cites 3 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Benefits of technology

The present patent relates to a computer system and method for solving geometric programming problems by using flexible vector-processing algorithms. The invention is based on the discovery of hidden properties of linearity, convexity, and separability in geometric programming problems and the development of qualitative and quantitative exploitations of these properties. The computer system and method involve reformulating the geometric programming problem as an equivalent generalized geometric programming optimization problem with only linear constraints and solving it by vector processing. The invention has applications in a variety of fields and can be implemented using computer programs and computer systems.

Problems solved by technology

In the 1960s, commercial electrical power distribution networks had sufficiently increased in scope and complexity to require electric utility companies to custom design and fabricate large-scale power-distribution transformers that would satisfy industrial and residential power demands.
Despite its substantial success, the utility of existing geometric programming techniques has been limited to moderate- and large-scale problems involving up to tens of thousands of decision variables, but its implementation for solution of extreme-scale (sometimes referred to as exa-scale or mult-scale) problems involving millions and even the billions of decision variables has not been practically achieved.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Flexible vector-processing algorithms for numerically solving extreme-scale, linear and non-linear, predictive and prescriptive, problems in science and engineering, on parallel-processing super computers
  • Flexible vector-processing algorithms for numerically solving extreme-scale, linear and non-linear, predictive and prescriptive, problems in science and engineering, on parallel-processing super computers
  • Flexible vector-processing algorithms for numerically solving extreme-scale, linear and non-linear, predictive and prescriptive, problems in science and engineering, on parallel-processing super computers

Examples

Experimental program
Comparison scheme
Effect test

example 1

[0060]Choosing D= and h(y)=(½)={Σ1nyj2} in the contracted version h:D of h:D implies that ∇h(y)=(y1, y2, . . . , yn)T is a solution χ to Aχ−b=0 when y=ycr, which must be an optimal solution to the convex quadratic minimization problem

Minimize(½)(zTA)(zTA)T−zTb for z∈

or, equivalently,

Minimize(½)zT(AAT)z−bTz for z∈

[0061]This problem, which is termed GMRES in the literature, is solvable via the conjugate-gradient algorithm when A has full row rank, but is likely best solved by other linear-algebraic methodology because any sparsity of A might be absent in AAT. The vector parallel-processing of the computation of yT from zT in this GGP Problem Q is enhanced by the completely separable form of this example function h:D, thereby establishing that GGP is clearly the superior methodology.

example 2

[0062]Choosing D= and h(y) to be a constant in the context of a system Aχ−b=0 known to have a non-zero solution χ shows that solutions χ cannot always be produced by a solution ycr of the dual GPP Problem Q (because ∇h(ycr)=0), unless h:D is carefully selected.

[0063]In particular, functions h:D that are guaranteed to produce at least one solution χ to every system Aχ−b=0 that has a solution are most easily described in terms of the conjugate transform g:C of the expanded version h:D of a given function h:D, wherein

C=x∈|supy∈D[xTy−h(y)]

and

g(x)=supy∈D[xTy−h(y)] for x∈C.

Such functions g:C and h:D are called “conjugate functions” because h:D is also the conjugate transform of g:C when h:D is closed and convex, a non-obvious symmetry that seems plausible because of the symmetry of the conjugate inequality

xTy≦g(x)+h(y) for each x∈C and each y∈D,

which is an elementary consequence of the preceding definition of g:C in terms of h:D.

[0064]Now, a non-obvious fact derivable from GGP duality t...

example 3

[0065]Choosing, as in the previous example,

D=and h(y)=(½){Σ1nyi2}+yn+1

implies, by differential calculus and the complete separation of h:D, that

C=×1 and g(x)=(½){Σ1nxi2}+0

and hence that this GGP approach produces at least one solution χ to every system Aχ−b=0 that has a solution.

[0066]Since there are infinitely many choices of closed convex functions h:D for which 0∈(int D), and for which C=×1, there are infinitely many GGP dual variational principles that can be used to solve a given system Aχ−b=0, all of which use vector parallel-processing of the computation of yT from zT. Considering the GP duality theory discussed above, it is noted that the conjugate inequality derived above clearly implies the duality inequality

0≦g(x)+h(y) for each z∈X∩C and each y∈Y∩D,

because X and Y are orthogonal complementary subspaces in . This inequality expresses the main part of the weak duality theorem for the following pair of generalized geometric programming dual problems:

Primal GGP Problem P:

[0...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

A computer-implemented method for numerical solution of a geometric programming problem is described, including the computer-implemented steps of: reformulating the geometric programming problem as an equivalent generalized geometric programming optimization problem with only linear constraints, and solving the equivalent generalized geometric programming optimization problem by vector processing, including determining by computer-implemented numerical computation a solution for an unconstrained objective function whose independent vector variable is the generalized geometric programming conjugate dual of a primal decision vector variable of the geometric programming problem, and includes a variable linear combination of fixed vectors enabling the vector processing. Also described are computer-readable storage devices, computer program products, and computer systems for such numerical solution methodology.

Description

CROSS-REFERENCE TO RELATED APPLICATIONS[0001]This is a continuation-in-part application under 35 U.S.C. §120 of International Patent Application No. PCT / US2015 / 023734 filed on Mar. 31, 2015, which in turn claims the benefit of U.S. Provisional Patent Application No. 61 / 973,232 filed on Mar. 31, 2014 in the name of Elmor L. Peterson for “FLEXIBLE VECTOR-PROCESSING ALGORITHMS FOR NUMERICALLY SOLVING EXTREME-SCALE, LINEAR AND NON-LINEAR, PREDICTIVE AND PRESCRIPTIVE, PROBLEMS IN SCIENCE AND ENGINEERING, ON PARALLEL-PROCESSING SUPER COMPUTERS”. The disclosures of International Patent Application No. PCT / US2015 / 023734 and U.S. Provisional Patent Application No. 61 / 973,232 are hereby incorporated by reference herein in their respective entireties.FIELD[0002]The present disclosure relates to new vector parallel-processing algorithms for numerically solving extreme-scale scientific and engineering problems not currently solvable in real time by previous algorithms whose computational complex...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F17/12G06F17/16G06F17/50
CPCG06F17/12G06F17/16G06F17/5045G06Q10/04G06Q30/02G06F17/11G06F30/30G06F30/00G06F9/30036G06F9/3877G06F2009/3883G06N7/02G06N7/01
Inventor PETERSON, ELMOR L.
Owner PETERSON ELMOR L
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com