Method of forming a model representative of the distribution of a physical quantity in an underground zone, free of the effect of correlated noises contained in exploration data
a technology a model is applied in the field of forming a model representative of the distribution of a physical quantity in an underground zone, free of the effect of correlated noises contained in exploration data, which can solve the problems of affecting the quality of the model estimated by solving the inverse problem, affecting the accuracy of the model, and no modelling operator is perfect, so as to achieve the effect of minimizing the cost function
a technology a model is applied in the field of forming a model representative of the distribution of a physical quantity in an underground zone, free of the effect of correlated noises contained in exploration data, which can solve the problems of affecting the quality of the model estimated by solving the inverse problem, affecting the accuracy of the model, and no modelling operator is perfect, so as to achieve the effect of minimizing the cost function
US7092823B2Inactive Publication Date: 2006-08-15INST FR DU PETROLE
Image
Smart Image Click on the blue labels to locate them in the text.
Smart ImageViewing Examples
Examples
Experimental program
Comparison scheme
Effect test
Embodiment Construction
[0050]Formulation of the Problem
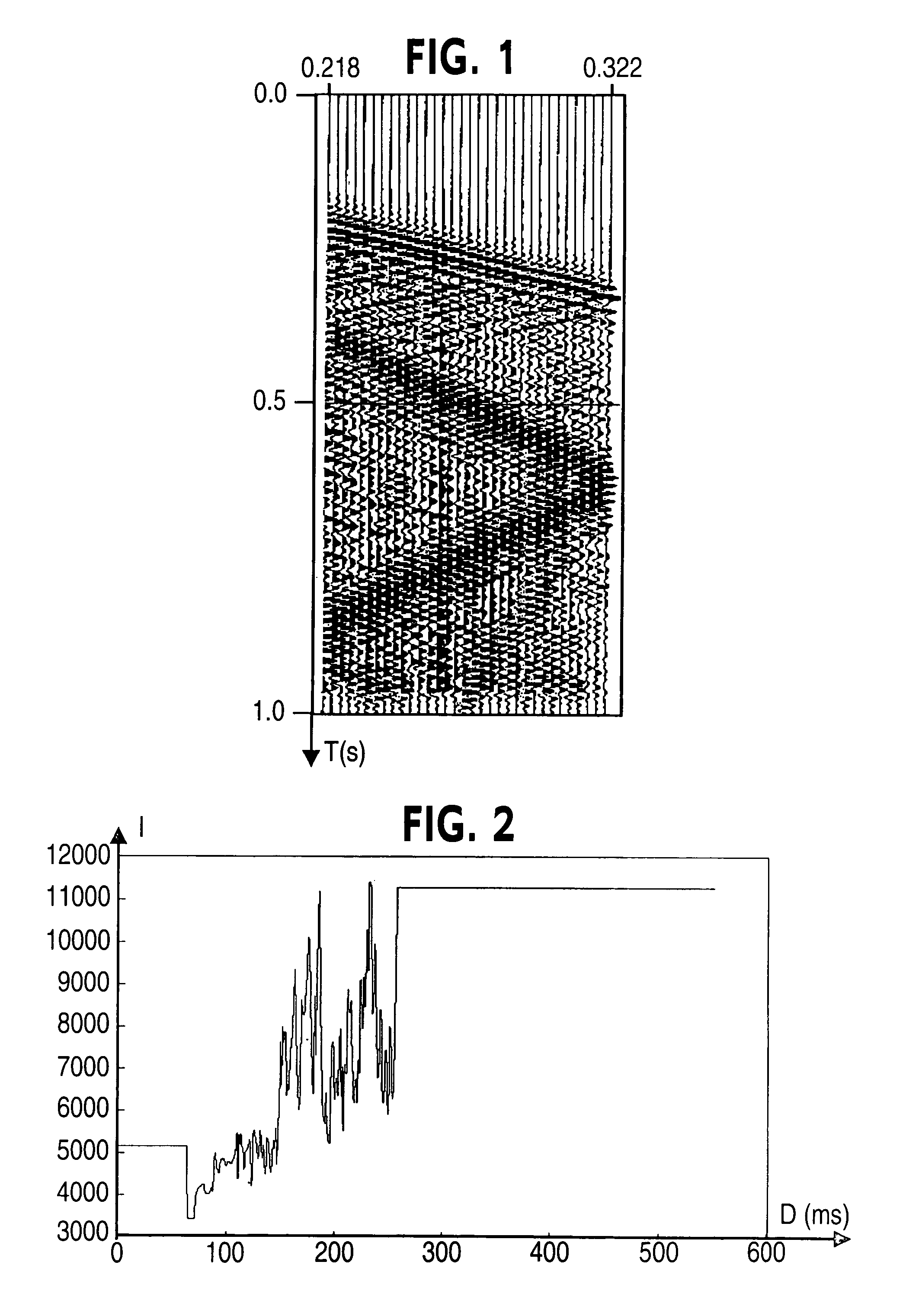
[0051]Data is available resulting from a sampled measurement of a function. This function depends on several variables (space or space-time variables for example).
[0052]These data, called d, correspond to measurements carried out to obtain information about a model m. They contain various noises:
[0053]correlated noises (or a superposition of correlated noises),
[0054]non correlated noises.
[0055]The problem is to determine quantitatively model m (or functions of this model) from data d.
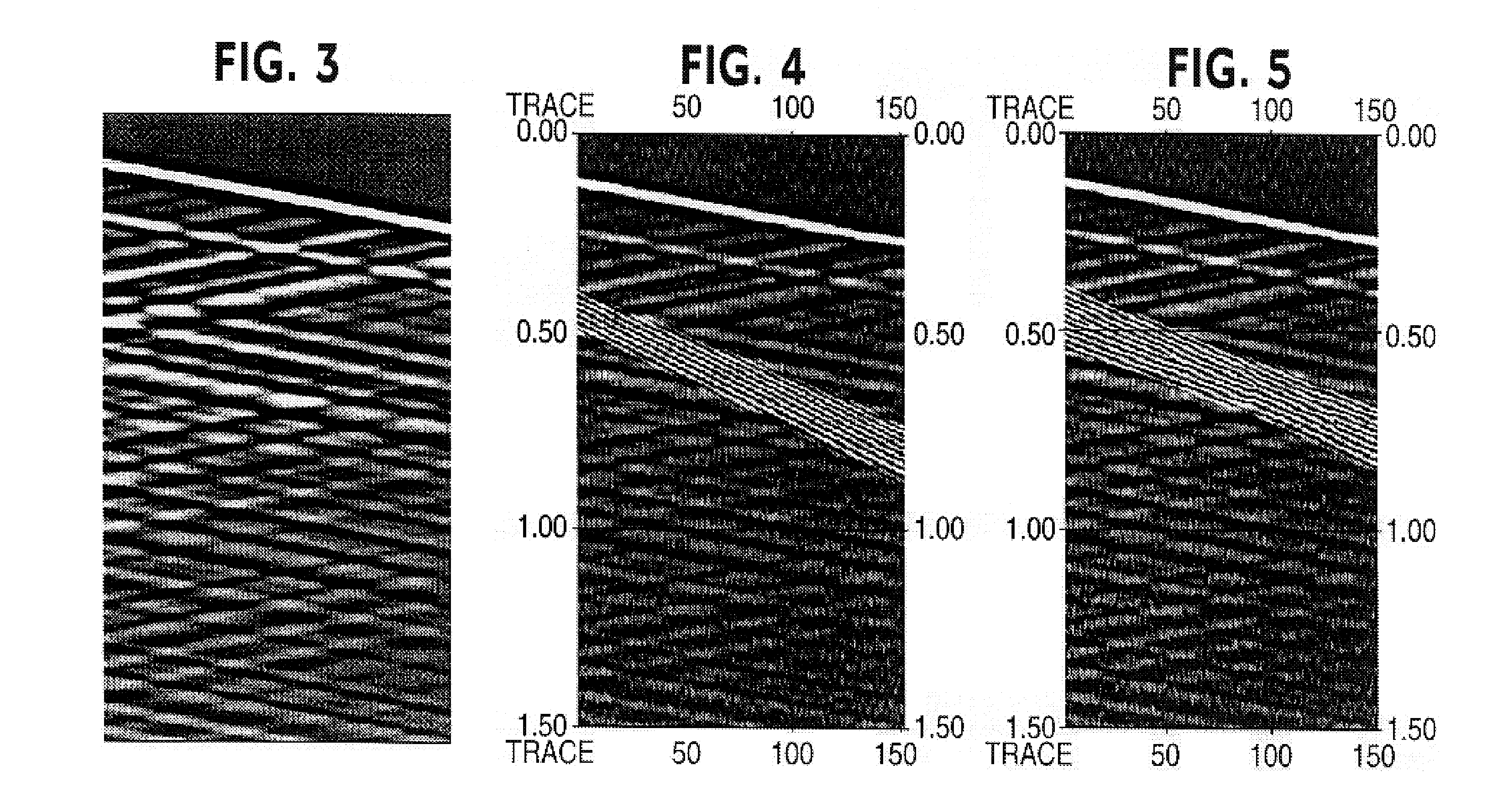
[0056]A modelling operator F is selected (linear or not) which associates with model m the response of the model. This operator actually models the real physical phenomenon only imperfectly. This is essentially (but not exclusively) the reason why correlated noises appear in the data: these noises correspond to a signal related to the model but the relation between them appears to be too complex to be included in modelling operator F, which should keep relatively simple f...
the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More PUM
Login to View More Abstract
The invention is a method of estimating, from data obtained by exploration of a zone of a heterogeneous medium, a model representative of a distribution, in the zone, of at least one physical quantity, the model being free of a presence of correlated noises that may be contained in the data which has application to determining the distribution in an underground zone of acoustic impedance, propagation velocities and permeabilities, etc. The method includes acquiring measurements giving information about physical characteristics of the zone; specifying a noise modelling operator which associates, with a model of each physical quantity, synthetic data that constitute a response of the model; selecting a noise modelling operator which associates a correlated noise with a noise-generating function belonging to a predetermined space of the noise-generating functions; specifying a norm or of a semi-norm in the data space; specifying a semi-norm in the space of the noise-generating functions; defining a cost function; and adjusting the model and of the noise-generating functions.
Description
BACKGROUND OF THE INVENTION[0001]1. Field of the Invention[0002]The present invention relates to a method of forming, from data obtained by exploration of a zone of a heterogeneous medium, a model representative of the distribution in the zone of a physical quantity (at least partly) free of the presence of correlated noises that may be contained in the data.[0003]The method applies, for example, to the quantification of the acoustic impedance in an underground zone.[0004]2. Description of the Prior Art[0005]The process of seeking a model that adjusts to experimental measurements has been developed in nearly all the fields of the sciences or technology. Such an approach is known under various names: least-squares method for parameters estimation, for inverse problem solution. For a good presentation of this approach within the context of geosciences, one may for example refer to:[0006]Tarantola, A.: “Inverse Problem Theory: Method for Data Fitting and Model Parameter Estimation”, El...
Claims
the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More Application Information
Patent Timeline
15 Aug 2006
Publication
US7092823B2
- IPC
- G01V3/18; G01V1/34; G01V1/36
- CPC
- G01V1/34; G01V1/36; G01V2210/32
- Inventors
- LAILLY, PATRICK; RENARD, FRANCOIS