Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Parallel matrix full-selected primary element Gauss-Jordan inversion algorithm based on multi-core DSP (Digital Signal Processor)

A technology of all-selected pivot and inverse algorithm, which is applied in the field of mobile communication, can solve the problems that the inverse matrix algorithm cannot satisfy all matrices, and cannot meet the requirements of high-speed operation, so as to improve the solution accuracy, fast operation speed, and small memory usage Effect

Inactive Publication Date: 2013-01-16
UNIV OF ELECTRONIC SCI & TECH OF CHINA
View PDF3 Cites 5 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0004] The purpose of the present invention is to overcome the defect that the algorithm about inversion matrix in the prior art cannot satisfy all matrices, and the existing matrix inversion algorithm can no longer meet the requirements of high-speed operation, and provides a multi-core DSP-based parallel matrix all-selection master Yuan Gaussian Jordan inversion algorithm, fully exploit the high-performance advantages of multi-core DSP, and solve the above defects

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Parallel matrix full-selected primary element Gauss-Jordan inversion algorithm based on multi-core DSP (Digital Signal Processor)
  • Parallel matrix full-selected primary element Gauss-Jordan inversion algorithm based on multi-core DSP (Digital Signal Processor)
  • Parallel matrix full-selected primary element Gauss-Jordan inversion algorithm based on multi-core DSP (Digital Signal Processor)

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

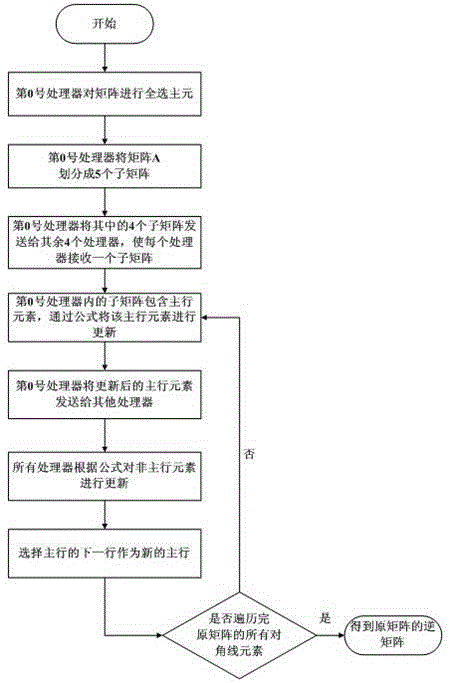
[0042] like figure 1 The parallel matrix inversion algorithm based on multi-core DSP is shown, which is Gaussian Jordan algorithm with all selected pivots, which occupies less memory, has fast operation speed and high precision, and is easy to implement in parallel.

[0043] Each update of the Gaussian Jordan inversion algorithm matrix element is based on the elements on the diagonal, and the elements are updated with different formulas for the elements in different columns, in the same column and different rows, and in different columns and rows. The row where the current diagonal element is located in each update is called the main row, each matrix element on the main row is called the main row element, and the rest of the matrix elements are called non-main row elements.

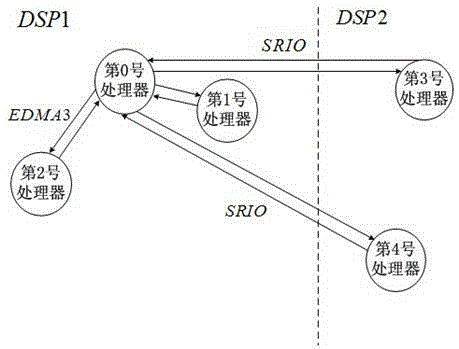
[0044] like figure 1 , 2 As shown, in this embodiment, j=5 block processors are used to invert the matrix A of order n, and the processors are numbered from 0 to 4. Among them, the digital signal proce...

Embodiment 2

[0065] The difference from Example 1 is that steps 3-5 are different.

[0066] The specific implementation of steps 3 to 5 in this embodiment is as follows:

[0067] Step 3: The processor with the main row in the sub-matrix is ​​the No. 1 processor, so the No. 1 processor uses the formula:

[0068]

[0069] and the formula:

[0070]

[0071] Update the main row elements, and use EDMA3 to send the updated main row elements to No. 2 processor, and use SRIO to send the updated main row elements to No. 3 and No. 4 processors, where the formula middle is the element value in the sub-matrix, is the element value in the updated sub-matrix, n is the number of sub-matrix rows, j is an integer and 0≤j image 3 As shown, the figure is a communication schematic diagram when the main row element is located in the No. 1 processor sub-matrix.

[0072] Step 4: The other processors use the formula according to the received updated main row element value:

[0073]

[0074] and th...

Embodiment 3

[0080] The difference from Example 1 is that steps 3-5 are different.

[0081] The specific implementation of steps 3 to 5 in this embodiment is as follows:

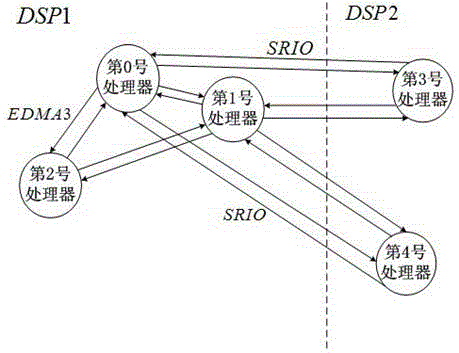
[0082] Step 3: The processor with the main row in the sub-matrix is ​​the No. 2 processor, so the No. 2 processor uses the formula:

[0083]

[0084] and the formula:

[0085]

[0086] Update the main row elements, and use EDMA3 to send the updated main row elements to No. 1 processor, and use SRIO to send the updated main row elements to No. 3 processors and No. 4 processors.

[0087] Step 4: After receiving the updated value of the main row element, the rest of the processors use the formula

[0088]

[0089] and the formula

[0090]

[0091] Update its sub-matrix, where i is an integer and 0≤i

[0092] Step 5: After the sub-matrix of processor No. 1, processor No. 3 and processor No. 4 is updated, processor No. 1 and processor No. 2 use EDMA3, and processor No. Processor 4 uses SRIO to sen...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides a parallel matrix full-selected primary element Gauss-Jordan inversion algorithm based on multi-core DSP (Digital Signal Processor), which solves the shortcoming that the current inversion matrix algorithm cannot meet all matrixes and cannot meet the requirement of high-speed operation. The method comprises the following steps: dividing a matrix A into p sub-matrixes, then transmitting the p sub-matrixes to processors No.1 to No.(p-1); updating the primary running elements through the processor with the current primary running element; transmitting the updated primary running elements to all the processors except for the processor No.0 and the current processor; updating the sub-matrixes through the processors No.1 to No.(p-1); returning the sub-matrixes to the processor No.0; and then selecting a running element following the previous primary running element as the new primary running element to repeat the process until all diagonal elements of the original matrix are taken as the primary running element. With the adoption of the scheme, the method provided by the invention can fullfill the inversion function for all matrixes and meet the requirement of high-speed operation.

Description

technical field [0001] The invention belongs to the field of mobile communication, and specifically relates to a multi-core DSP-based Gaussian Jordan inversion algorithm for all selected pivots of a parallel matrix. Background technique [0002] Matrix inversion is a commonly used and cumbersome calculation process in engineering practice. There are many kinds of common matrix seeking algorithms, and the complexity of most of them can meet the requirements of general engineering applications. However, with the increasingly complex applications, these matrix inversion algorithms can no longer meet the requirements of high-speed operations. [0003] Therefore, in order to meet the requirements of high-speed operation of matrix inversion in the prior art, some high-speed inversion algorithms have been proposed, but these algorithms are all implemented for some special matrices, such as for three-diagonal matrix, five-diagonal matrix and The algorithm of triangular matrix inver...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F17/16
Inventor 王坚李玉柏李桓杨凯琪
Owner UNIV OF ELECTRONIC SCI & TECH OF CHINA
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com