Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Local linear embedded algorithm based radio frequency map unsupervised classifying method

A local linear embedding, radio frequency map technology, applied in computing, special data processing applications, instruments, etc., can solve the problem of high labor cost

Active Publication Date: 2013-08-21
哈尔滨工业大学高新技术开发总公司
View PDF2 Cites 14 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0007] In order to solve the problem that the existing radio frequency map classification method can only rely on the spatial layout of the area to be positioned for classification, the labor cost required for classification is relatively high, and at the same time, different understandings of the spatial layout will produce different classification schemes. subjectivity of the problem, thus providing an unsupervised classification method for radio frequency maps based on local linear embedding algorithm

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Local linear embedded algorithm based radio frequency map unsupervised classifying method
  • Local linear embedded algorithm based radio frequency map unsupervised classifying method
  • Local linear embedded algorithm based radio frequency map unsupervised classifying method

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

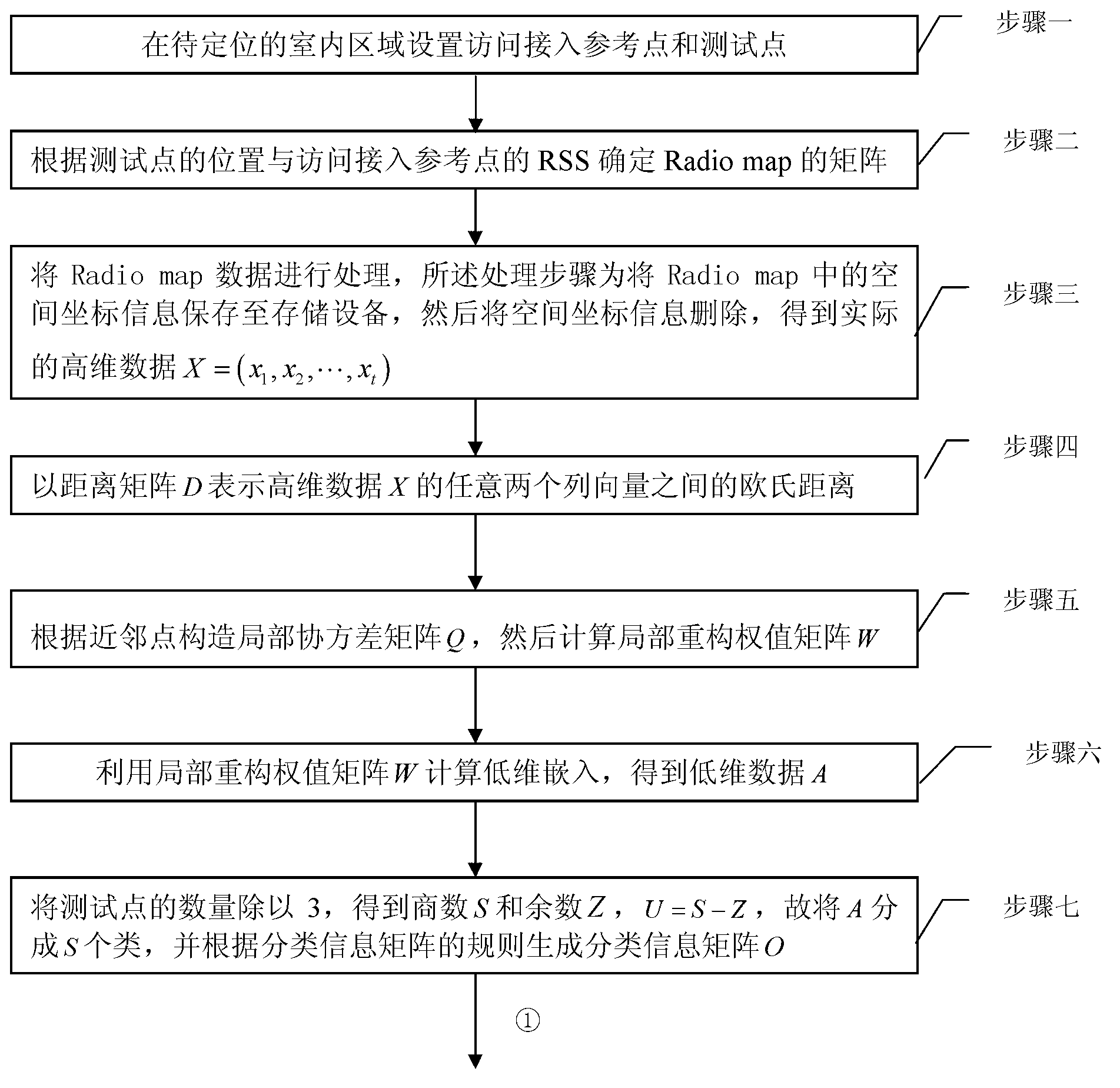
[0041] Specific implementation mode 1. Combination figure 1 This specific embodiment will be described. A radio frequency map unsupervised classification method based on local linear embedding algorithm, it comprises the following steps:

[0042] Step 1: Set access reference points and test points in the indoor area to be positioned, the height of the access reference points is 2-2.5 meters from the ground, and the density of test points is 3-5 points / square meter;

[0043] Step 2: Determine the matrix of the Radio map according to the position of the test point and the RSS of the access reference point;

[0044] If there are t test points in total, the Radio map is α=(α 1 , α 2 ,...,α j ,...,α t ), α 1 , α 2 ,...,α t Both are column vectors, j is the sequence of test points; where, α 1，j , α 2，j They are the abscissa and ordinate of the spatial position of the jth test point, respectively, and the spatial information of the test point is continuous; the continuous s...

specific Embodiment approach 2

[0071] Embodiment 2. This embodiment is different from Embodiment 1 in that the value of the K column vectors in Step 4 is K=6 or 7.

specific Embodiment approach 3

[0072] Embodiment 3. The difference between this embodiment and Embodiment 1 is that the calculation process of the intra-class divergence θ described in step 9 is:

[0073] Set the center of the class, which is the point in a class with the smallest Euclidean distance sum to all points of the class;

[0074] Let B=(b 1 , b 2 ,...,b i ,...,b n ) is a category, and b m is the center of class B, and the intra-class divergence θ is the center b m The average of the Euclidean distances to all points in B, namely

[0075] θ = Σ i = 1 n d ( b m , b i ) n - - - ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to a local linear embedded algorithm based radio frequency map unsupervised classifying method and aims at solving the problem that existing radio frequency map classifying methods can only depend on space distribution of a to-be-positioned area for classification. The method includes setting an access reference point and a test point in a to-be-positioned indoor area; determining a matrix of a Radio map according to the position of the test point and RSS (radio-frequency signal strength) of the access reference point; processing data of the Radio map, namely, storing space coordinate information in the Radio map into storage equipment, and deleting the space coordinate information to acquire actual high-dimension data X=(x1, x2, ..., xt); and building a local covariance matrix Q according to adjacent points, calculating low-dimension embedding by utilizing a local reconstruction weigh matrix W, dividing low-dimension data into S classes and judging inter-class divergence and in-class divergence, merging the classes according to ratio conditions, and acquiring a final class information matrix. The local linear embedded algorithm based radio frequency map unsupervised classifying method can be widely applied to unsupervised classification of radio frequency maps.

Description

technical field [0001] The invention relates to a classification method of a local linear embedding (Locally Linear Embedding, LLE) algorithm. Background technique [0002] With the advancement of science and technology and the acceleration of urbanization, the space for human activities has shifted from outdoors to indoors, and people's requirements for positioning services, especially indoor positioning services, are also increasing. How to determine the spatial coordinates of a mobile terminal and its holder in a complex indoor environment has become an urgent problem to be solved. However, due to the complexity of the indoor environment, especially the existence of small-scale fading and interference factors, traditional outdoor positioning methods are difficult to apply in indoor scenes, and the accuracy is difficult to meet the requirements. [0003] Although indoor positioning methods such as ultrasonic positioning technology, infrared positioning technology, and ult...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06F17/30
Inventor 马琳栾斌徐玉滨崔扬孟维晓莫云
Owner 哈尔滨工业大学高新技术开发总公司
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com