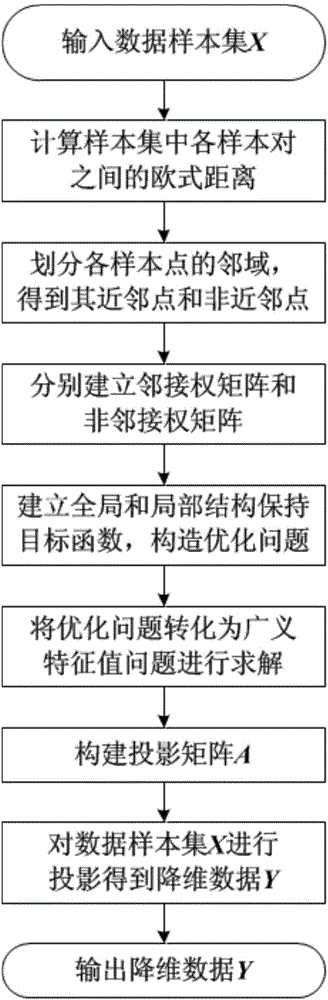
Data dimension reduction method based on data global-local structure preserving projections
A local structure and projection-preserving technology, applied in electrical digital data processing, special data processing applications, instruments, etc., can solve the problem of only focusing on the global data or the loss of local feature data feature information
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
example
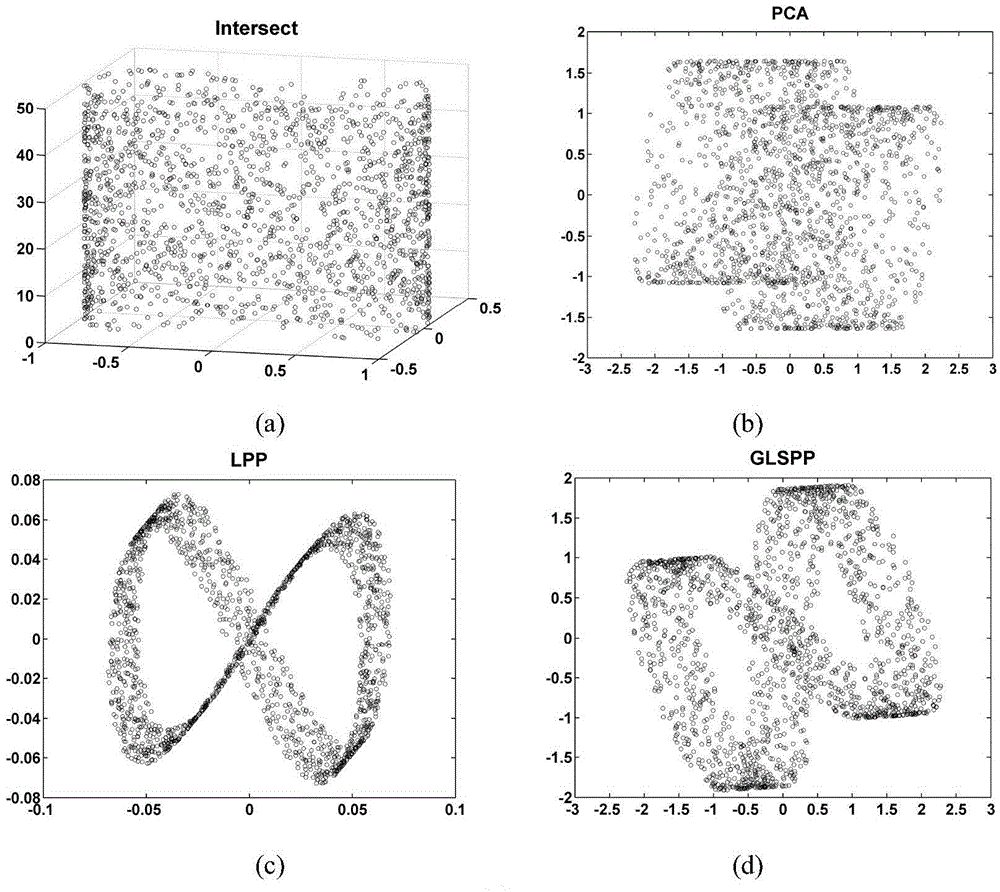
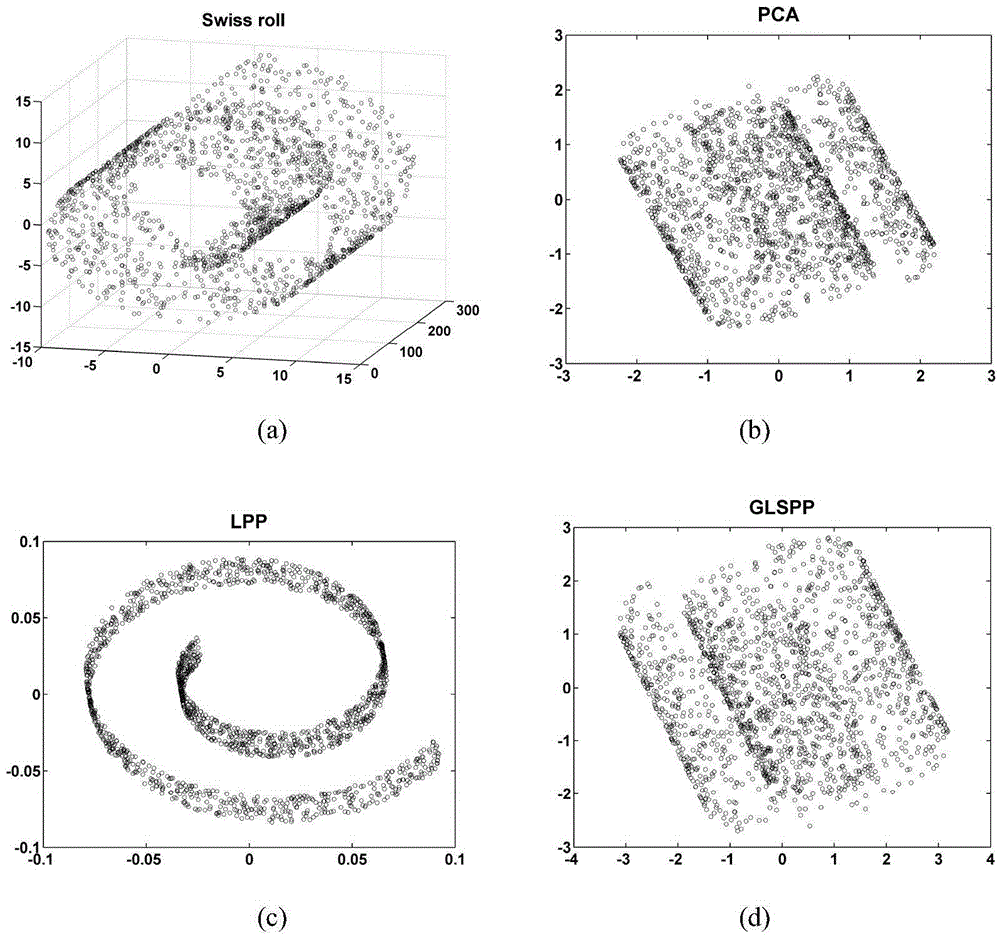
[0056] Example: The following two synthetic data, Intersect and Swiss roll, are used as examples to illustrate the superiority of the present invention. The sample sets of Intersect and Swiss roll data are both composed of 1800 sample points. The dimension of the original data space is 3, and the dimension of the data space after dimension reduction is 2. The generating function of Intersect data is: t=2π*[1:n]’ / n, X=[cos(t)0.5*cos(t).*sin(t)50*rand(n,1)]. The generating function of Swiss roll data is: t=3π / 2*(1+2*rand(n,1)), X=[t.*cos(t)300*rand(n,1)t.*sin( t)]. Select PCA and LPP to compare with GLSPP, and use the k-nearest neighbor method to define the neighborhood of data points, and k is set to 15.
[0057] figure 2 and image 3 They are the visualization effects of Intersect and Swiss roll data sample sets reduced to 2D under different algorithms. It can be seen that PCA projects the sample data along the direction of maximum variance, which basically maintains the...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com