Unconstrained static structural analysis method based on Householder transformation
A static analysis and unconstrained technology, applied in special data processing applications, instruments, electrical digital data processing, etc., can solve problems such as low efficiency, high efficiency, and low precision
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment
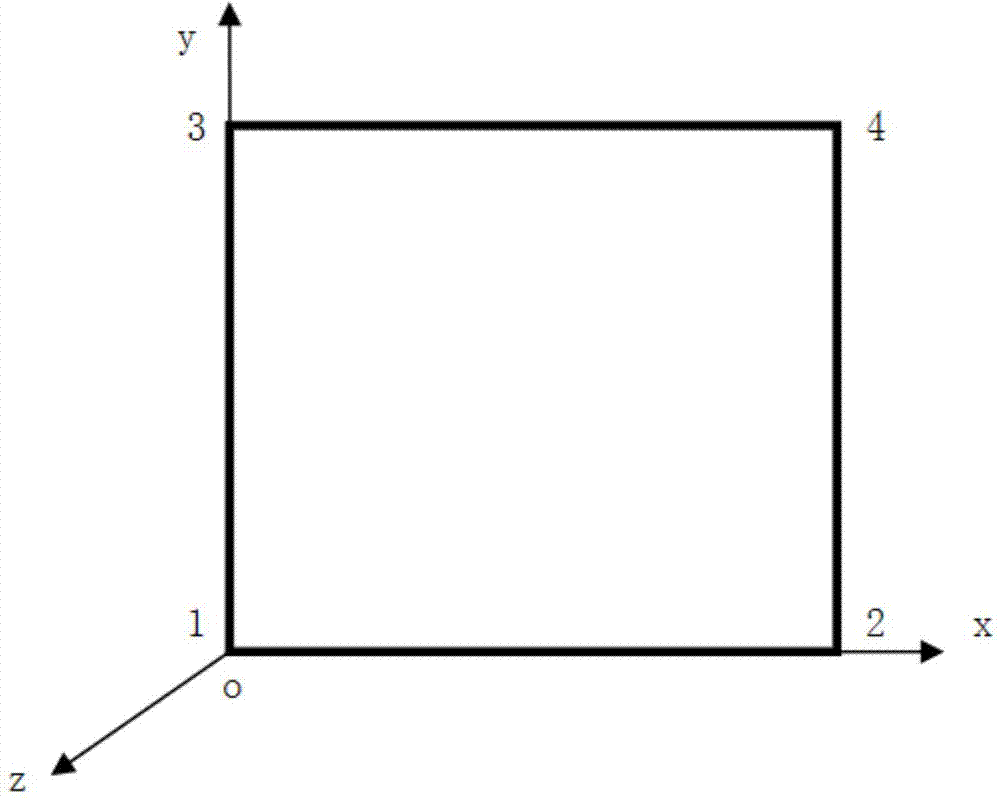
[0099] This example is a figure 2 A planar problem composed of quadrilateral shell elements is shown, one material. Abaqus element type: S4R. The element size is 1*1m, the thickness is 0.01m, and the material parameters are: elastic modulus E=1.0, Poisson's ratio μ=0.3.
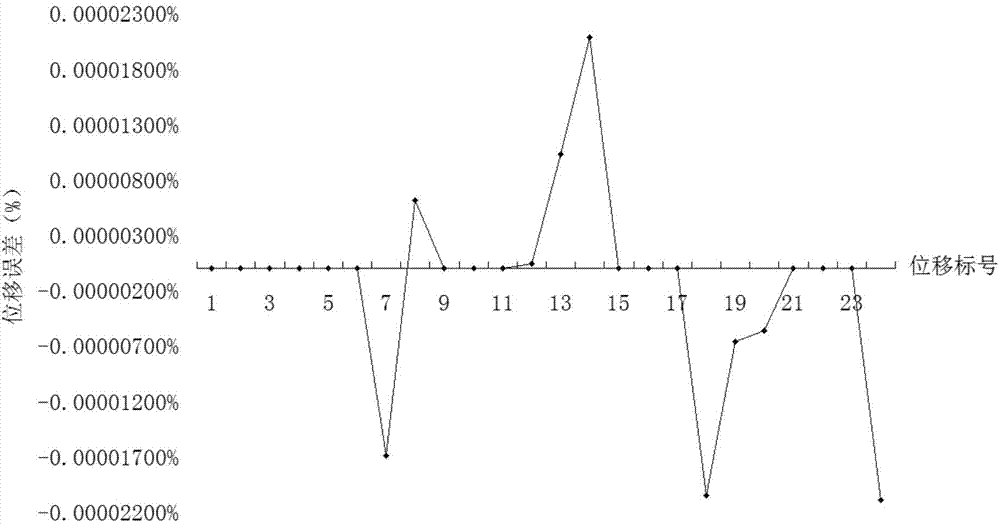
[0100] In Abaqus, a fixed boundary condition is applied to the nodes 1 and 3 at the left end of the above unit, and a pulling force is applied to the nodes 2 and 4 at the right end. Calculate the support reaction force and support reaction moment of each node of the unit, which is used as the right-hand term F of the external load of the unconstrained problem solved by this method, which is equivalent to the constrained static force in Abaqus.
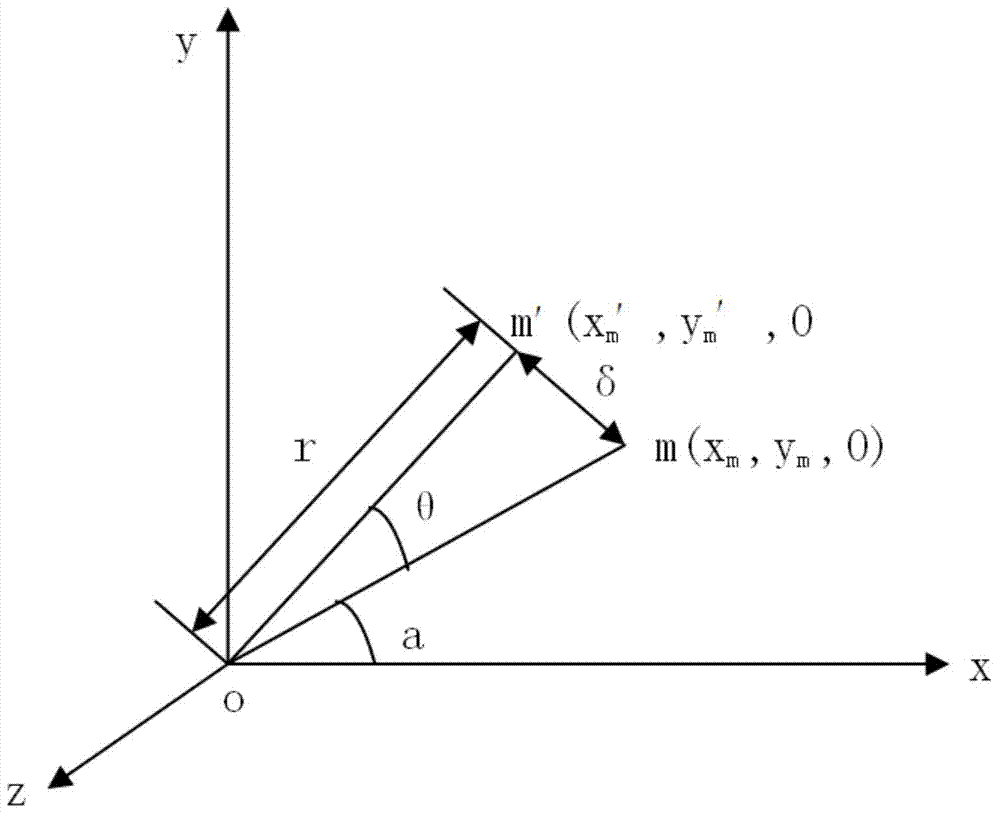
[0101] According to the displacement formula of the shell element and the plane strain and bending strain of the shell are 0, write the rigid body displacement of the above element, please refer to the principle figure 1 shown. Assuming that the whole structure i...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com