Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

A Phase Diagram Matrix Method for Nonlinear Dynamic Behavior Analysis

A non-linear dynamics and behavior analysis technology, applied in the field of data recognition, it can solve the problem that ergodicity cannot be quantitatively analyzed, and achieve the effect of improving the speed of identification and the calculation process.

Active Publication Date: 2017-04-12
SHIJIAZHUANG TIEDAO UNIV
View PDF6 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0007] The technical problem to be solved by the present invention is to provide a phase diagram matrix method for nonlinear dynamic behavior analysis, which can overcome the shortcomings of the ergodicity of nonlinear dynamic behavior that cannot be quantitatively analyzed, and can quantitatively measure the nonlinear system The ergodic feature simplifies the large amount of calculations required for system chaos identification and improves the identification speed and accuracy of system chaos state

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • A Phase Diagram Matrix Method for Nonlinear Dynamic Behavior Analysis
  • A Phase Diagram Matrix Method for Nonlinear Dynamic Behavior Analysis
  • A Phase Diagram Matrix Method for Nonlinear Dynamic Behavior Analysis

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0047] The equation of the Duffing system is:

[0048]

[0049] Where δ≥0 is the damping coefficient, and γ is the amplitude of the built-in periodic driving force. The equation behaves as a chaotic state under some parameter values. The existing methods of judging the state of the system by using the change of the phase trajectory mainly determine the state of the system by observing the phase trajectory of the system. This method is very dependent on people's subjective cognition, there is no quantitative standard, the generality is not good, and the operability is not high.

[0050] The specific operation steps of using this method to judge the system status are as follows:

[0051]The first step, after setting the parameters in the system to ω=1, δ=0.5, γ=0.66, and the system calculation step size h=0.01 seconds, regard the system displacement time series as x and velocity time series as y, The state of the Duffing system at a certain moment is (x, y), and a time ser...

Embodiment 2

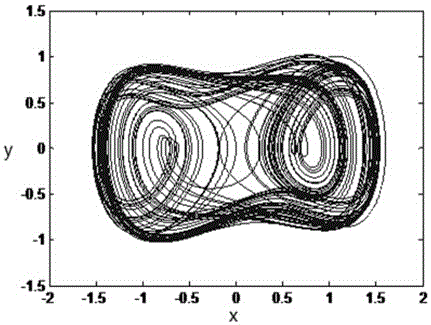
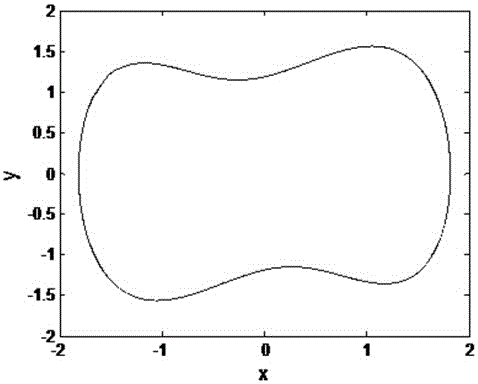
[0066] The difference from Example 1 is that γ in the Duffing equation is set to 0.98, and the phase space of the system is as follows image 3 shown. The graphical display of the phase diagram matrix obtained by this method is as follows Figure 4 As shown, the ergodic parameter s=0.0824 of the system in this state is obtained through calculation. Compared with the threshold of chaos discrimination thresh=0.35, it can be seen that the system is not in a chaotic state. The result of the fact is that the system is in a large-scale state at this time. The graphical display of graph matrix confirms this conclusion at the same time, which also shows the effectiveness and correctness of this method.

Embodiment 3

[0068] The difference from Embodiment 1 is that the size of the phase diagram matrix is ​​set to 100×100. The graphical display of the phase diagram matrix obtained by this method is as follows Figure 5 As shown, the ergodic parameter s=0.5462 of the system in this state is obtained through calculation. Compared with the threshold value of thresh=0.35, it can be seen that the system is in a chaotic state. The result of the fact is that the system is in a chaotic state at this time. The graphical display of graph matrix confirms this conclusion at the same time, which also shows the effectiveness and correctness of this method.

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a phase diagram matrix method for nonlinear dynamic behavior analysis, belonging to the technical field of data identification. The invention proposes a new phase diagram matrix method for analyzing the nonlinear dynamic behavior, which can analyze the nonlinear dynamic behavior from the perspective of ergodicity, and then identify the chaotic state of the system. This method pioneered the ergodic parameter, which can quantitatively describe the ergodic characteristics of the chaotic dynamic behavior, and the calculation process is fast and simple, which can greatly improve the identification speed of the chaotic state; this method also proposes a phase diagram matrix and The size of the phase diagram matrix can be set by yourself, and the ergodicity of the system phase space can be investigated from different scales. This method has important application value in the analysis of nonlinear system dynamics, especially in the identification of chaotic behavior.

Description

technical field [0001] The invention belongs to the technical field of data identification. Background technique [0002] Nonlinear science is known as the "third revolution" of natural science in the 20th century, and the research on nonlinear science has developed rapidly in recent years. The study of nonlinear science not only has great scientific significance, but also has broad application prospects. It involves almost every field of natural science and social science, and is changing people's traditional view of the real world. [0003] Chaos is a field that is very active and has broad application prospects in nonlinear science. Over the past 20 years, chaos has developed rapidly at an unprecedented speed into a modern subject with rich nonlinear physics background and profound mathematical connotation. [0004] Chaos is a quasi-random phenomenon in deterministic systems, which has the following main characteristics: (1) extreme sensitivity to initial conditions; (2...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G06F17/16
Inventor 赵志宏杨绍普王扬
Owner SHIJIAZHUANG TIEDAO UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com