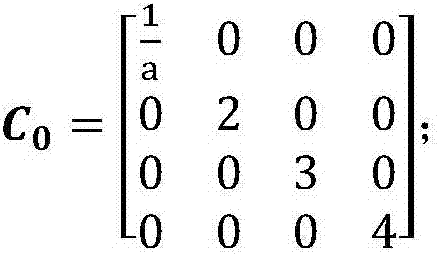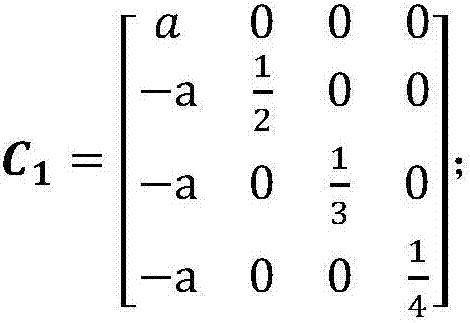Method for processing zero denominator condition of matrix inversion lemma, and method for recursively solving inverse matrix level by level
A technology for matrix inversion and inverse matrix, applied in the field of matrix recursion inversion, which can solve the problems of invalid matrix with large condition number and inability to perform calculation, etc.
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
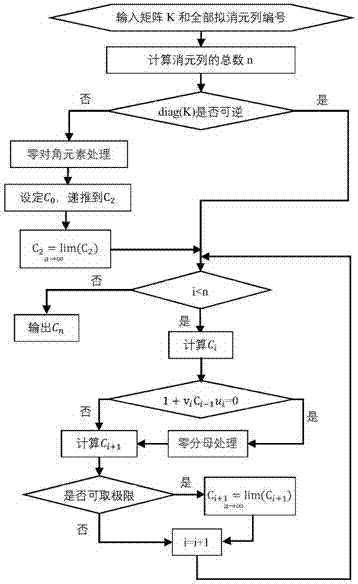
[0016] The following two calculation examples are combined to give the matrix recursive inversion process in detail. The calculation example 1 is for the zero principal element, and the calculation example 2 is for the zero denominator in the calculation process.
[0017] Calculation example 1. Suppose Recursively solve the elimination matrix at all levels.
[0018] ① Calculate C 0 :
[0019] because Medium K 1,1 = 0, it is impossible to find the inverse directly, let
[0020]
[0021] ② Calculate C 1 :
[0022] u 1 =[0,2,3,4] T ,v 1 =[1,0,0,0], 1+v 1 ·C 0 u 1 = 1,
[0023]
[0024] ③ Calculate C 2 :
[0025] u 2 =[2,0,5,6] T ,v 2 =[0,1,0,0],
[0026] Take the limit
[0027] ④ Calculate C 3 :
[0028] u 3 =[3,5,0,7] T ,v 3 =[0,0,1,0],
[0029]
[0030] ⑤ Calculate C 4 :
[0031] u 4 =[4,6,7,0] T ,v 4 =[0,0,0,1],
[0032] Verify the correctness of the elimination matrix at all levels and the C 4 = K -1 .
[0033] Calcu...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com