Supercharge Your Innovation With Domain-Expert AI Agents!

Task distribution system model of privacy protection space crowdsourcing and realization method

A technology for privacy protection and task allocation, applied in the computer field, it can solve problems such as only considering worker location privacy, not taking it into account, and unsatisfactory allocation results.

Active Publication Date: 2017-10-17
SHENZHEN UNIV
View PDF5 Cites 12 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

First, it only considers the location privacy of workers, not the privacy of task locations
Second, it mainly performs task assignment based on the worker's traveling distance without taking into account other important factors such as the worker's traveling speed, which makes the assignment results sometimes unsatisfactory

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Task distribution system model of privacy protection space crowdsourcing and realization method
  • Task distribution system model of privacy protection space crowdsourcing and realization method
  • Task distribution system model of privacy protection space crowdsourcing and realization method

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

[0051] The present invention is described in further detail now in conjunction with accompanying drawing. These drawings are all simplified schematic diagrams, which only illustrate the basic structure of the present invention in a schematic manner, so they only show the configurations related to the present invention.

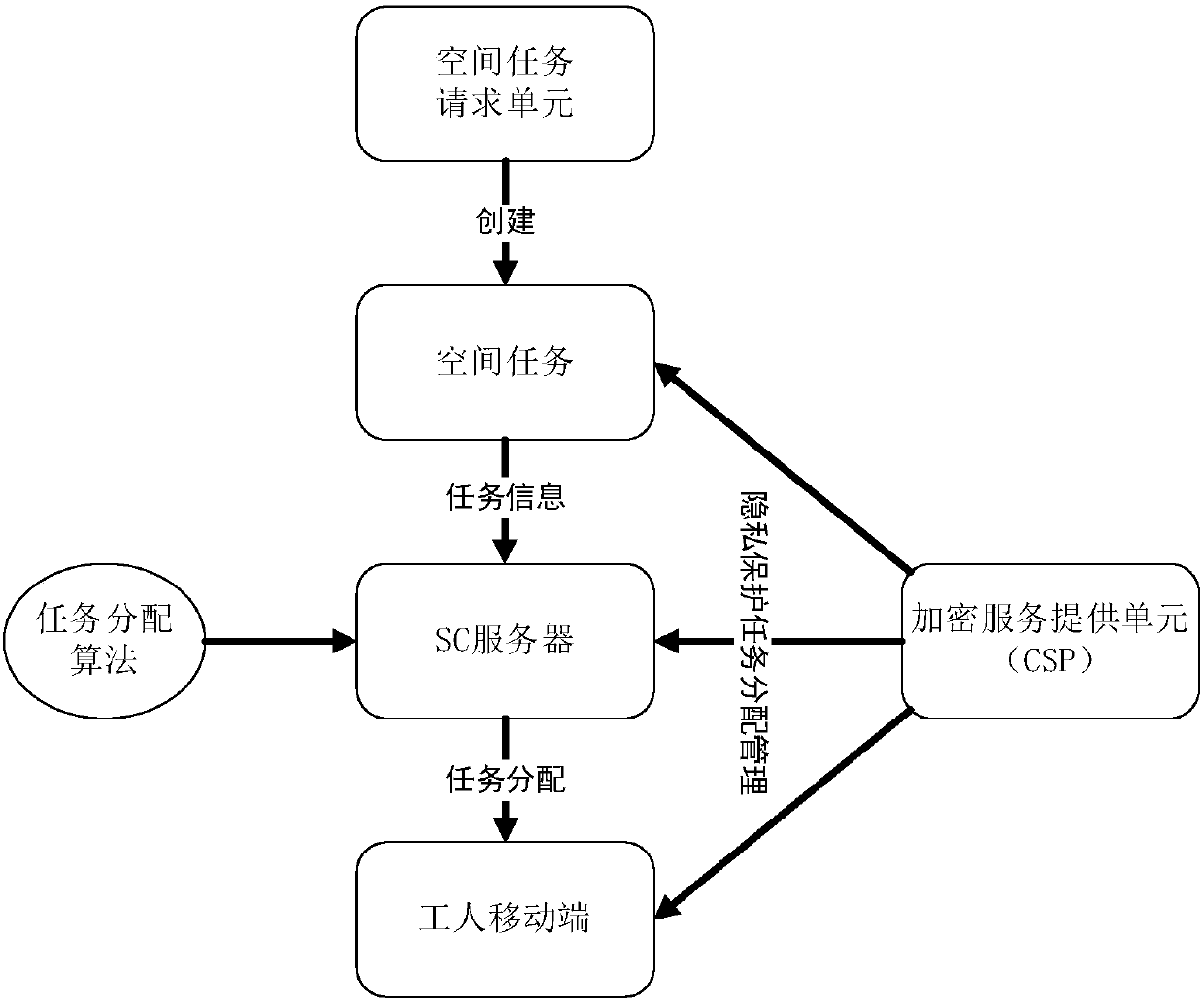
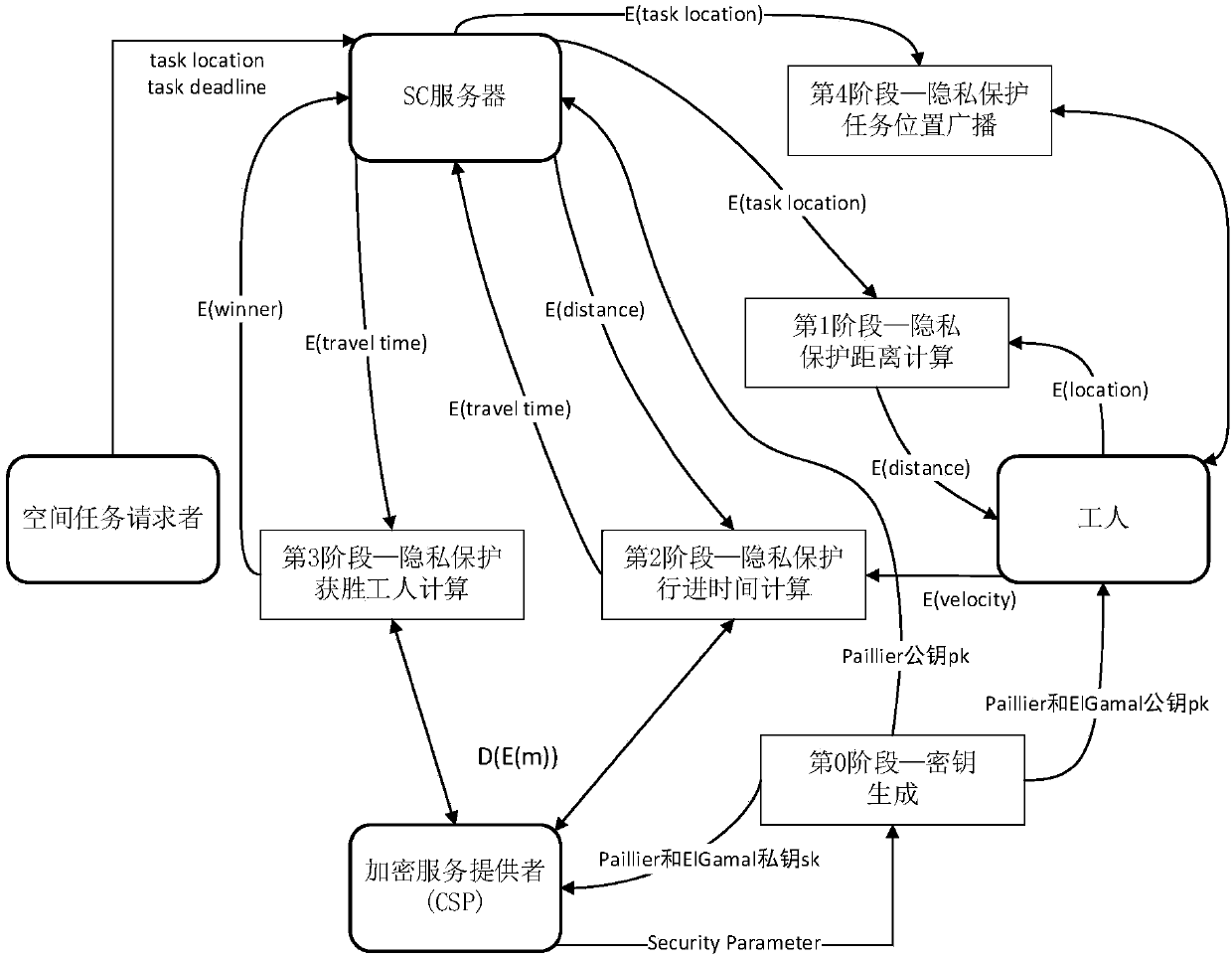
[0052] 1. System model and problem definition

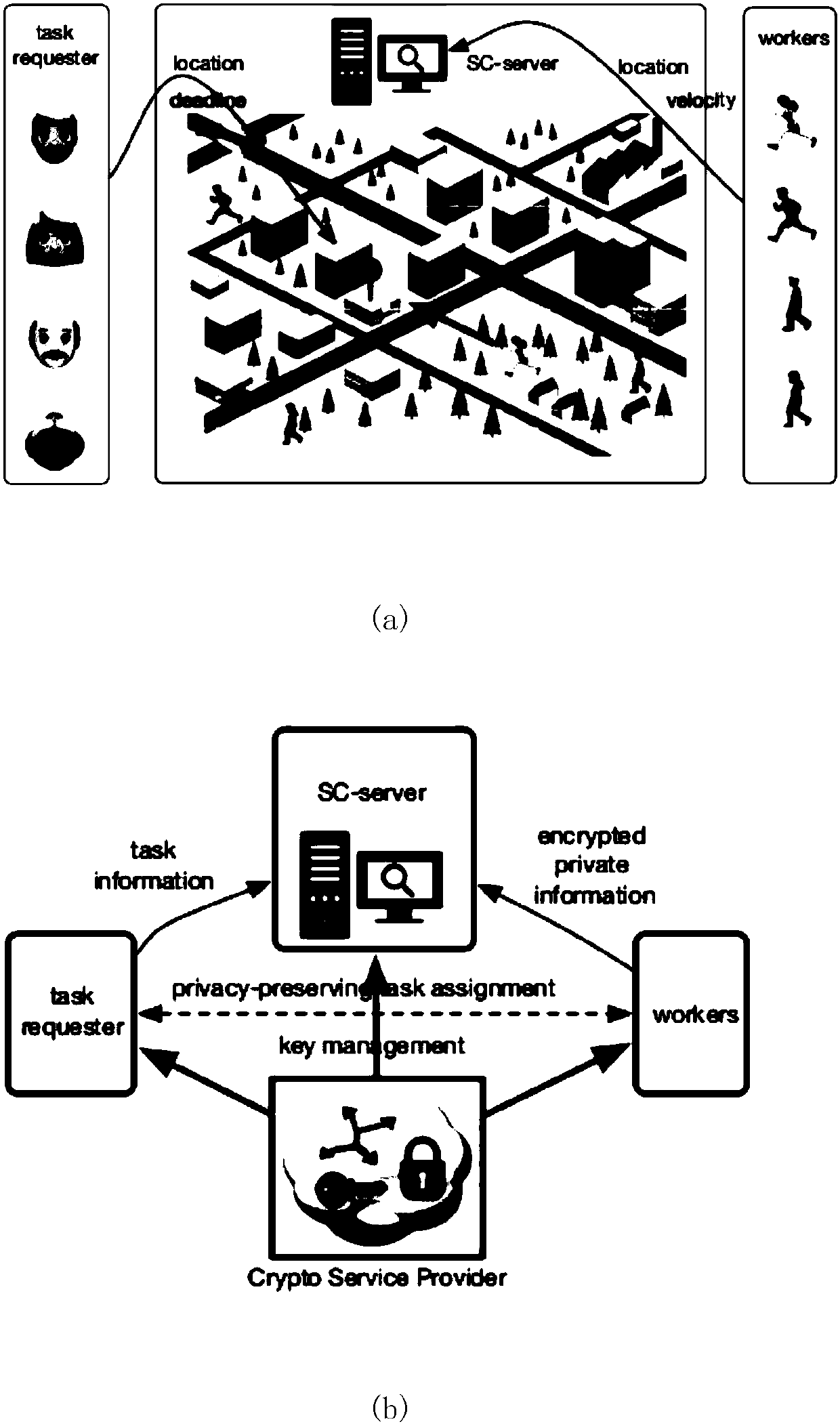
[0053] figure 1 A system model for spatial crowdsourcing is described. For non-private space crowdsourcing (see figure 1 (a) There are three components, namely SC server (SC-server), workers (workers) holding mobile devices and space task requester (taskrequester). The SC server is responsible for assigning appropriate workers to space tasks created by task requesters. Workers need to report their private information (such as location and velocity) to the SC server through their mobile devices. Based on this framework, we give the following definitions.

[0054] Definition 1 (space mission) space mission s ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a task distribution system model of privacy protection space crowdsourcing. The task distribution system model comprises a space outsourcing server, an encryption service providing unit, a space task request unit and a worker mobile terminal; the space task request unit is used for creating the space task, and transmitting the task information to the space crowdsourcing server; the space outsourcing server is used for distributing the task to the worker mobile terminal; the encryption service providing unit is used for providing the privacy protection task distribution management for the space task request unit, the space crowdsourcing server and the worker mobile terminal. Furthermore, the invention further discloses a realization method of the system model. The system model firstly realizes the dual-party privacy protection in the space crowdsourcing, not only protects the privacy of the worker, but also protects the task privacy. The efficient task distribution is performed in the space crowdsourcing, and the privacy protection on two aspects of the worker and the task is provided.

Description

technical field [0001] The invention belongs to the field of computers, and specifically relates to a task distribution system model of space crowdsourcing, in particular to a task distribution system model of privacy protection space crowdsourcing; in addition, the present invention also relates to the task distribution system of privacy protection space crowdsourcing The implementation method of the model. Background technique [0002] Crowdsourcing has revolutionized the problem-solving landscape by outsourcing a task (usually performed by a designated agent) to the masses through an open call. Crowdsourcing can provide on-demand talent capacity and expert services at a much lower cost than hiring professionals, and has been successfully applied to transcribing books, protein folding, galaxy classification, and traffic monitoring. Recently, crowdsourcing has also been widely used in emergency management, as it enables efficient and low-cost collection of critical informa...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): H04L29/08H04L29/06H04L9/06H04L9/00
CPCH04L63/0442H04L67/10H04L9/0643H04L9/008H04L67/52
Inventor 毛睿李荣华陆敏华王毅罗秋明商烁
Owner SHENZHEN UNIV
Features
  • R&D
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com