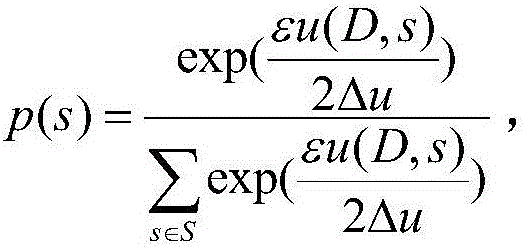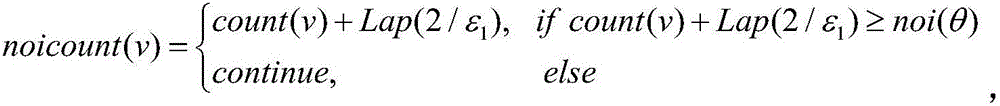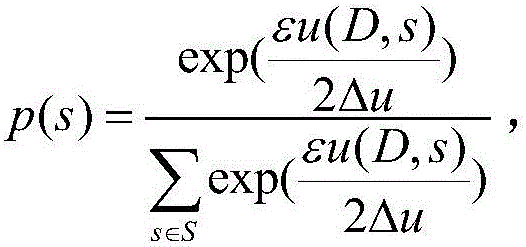Method for constructing decision tree based on differential privacy protection

A differential privacy and decision tree technology, applied in digital data protection, instrumentation, electrical digital data processing, etc., can solve the problems of inefficient selection methods and depletion of privacy budget, so as to protect privacy, improve accuracy, and reduce rapid consumption Effect

Inactive Publication Date: 2017-12-29
RENMIN UNIVERSITY OF CHINA
View PDF0 Cites 16 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, they mainly have two shortcomings: 1) decision classification is only performed on small spatial data. When the data points reach millions of levels, a large number of classification trees will be generated, res

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method for constructing decision tree based on differential privacy protection
  • Method for constructing decision tree based on differential privacy protection
  • Method for constructing decision tree based on differential privacy protection

Examples

Experimental program
Comparison scheme
Effect test

Example Embodiment

[0019] The present invention will be described in detail below in conjunction with the examples.

[0020] The present invention provides a method based on differential privacy protection decision tree, which aims at the differential privacy protection of the classic greedy decision tree C4. A protection mechanism alters this answer in a way that preserves the privacy of everyone in the dataset. The present invention comprises the following steps:

[0021] 1) Use Bernoulli (Bernoulli) random sampling principle to sample the original data set with sampling probability p to obtain a data set sample, and the obtained data set satisfies ln(1+p(e ε -1))- Differential privacy:

[0022] Perform Bernoulli random sampling on the original data set with the assumed sampling probability p, put the selected samples into the spatial samples, otherwise discard them, and calculate the privacy budget ε required to build the entire decision tree under the sampling probability p p . Among the...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

PUM

No PUM Login to view more

Abstract

The invention relates to a method for constructing a decision tree based on differential privacy protection. The method comprises the steps that sampling is performed on an original dataset according to a sampling probability p to obtain dataset samples, and the obtained dataset meets the requirement for ln(1+p(e<epsilon>-1)-differential privacy, wherein primary processing is performed on the dataset obtained through sampling, and continuous properties and discrete properties are made to jointly participate in decision selection under privacy protection; a C4.5 decision tree is initialized according to extracted dataset samples, and a sparse vector method is utilized to judge whether nodes in the decision tree continue to split; and the decision tree is constructed recursively. Through the method, classification accuracy is high, and the decision tree can be constructed efficiently and accurately while privacy is protected.

Description

technical field [0001] The invention relates to a decision tree privacy protection method, in particular to a method based on differential privacy protection decision tree. Background technique [0002] With the development of hardware and technology, it is not a difficult problem to collect a large amount of data in a timely and effective manner, but how to mine useful knowledge and value from these data is a difficult point for people to study. Classification algorithm is a commonly used data mining tool. It can well support applications such as precise marketing, personality preference and credit analysis, and is widely loved by the financial industry and companies. Decision tree is one of the common classification algorithms. When building a decision tree, you first need to decide which attribute to split the node on. This decision is dominated by the data in the node. In addition, once the decision tree is constructed, the leaf nodes can output count information about ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

Application Information

Patent Timeline
no application Login to view more
IPC IPC(8): G06F21/62G06K9/62
CPCG06F21/6245G06F18/24323G06F18/2415
Inventor 孟小峰郭胜娜
Owner RENMIN UNIVERSITY OF CHINA
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Try Eureka
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap