A Method of Aerodynamic Shape Optimization Based on Flow Field Prediction
A technology of aerodynamic shape and optimization method, applied in the direction of constraint-based CAD, design optimization/simulation, instrument, etc., can solve the design quality dependence, the data information cannot be fully utilized, and weaken the ability of the proxy model to capture the essential characteristics of the real model, etc. It can improve the convergence speed and overall efficiency, avoid sampling and simulation calculation, and save the cost of optimization time.
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
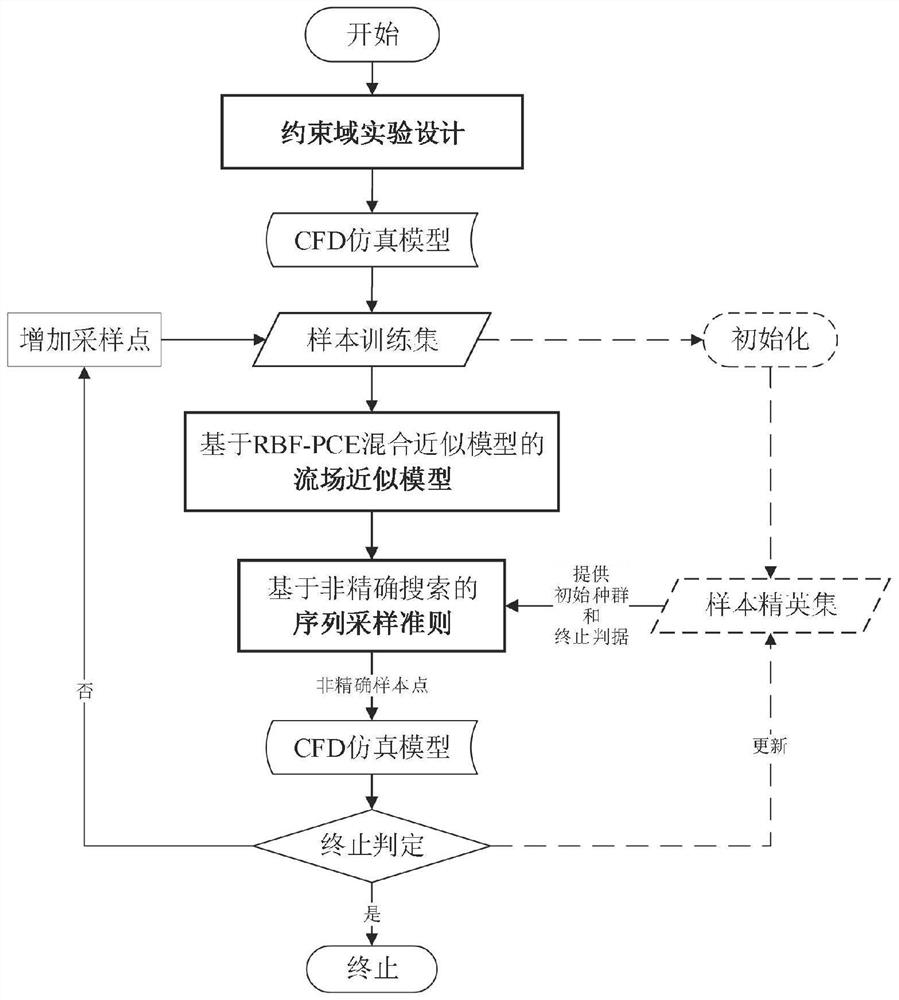
Image
Examples
Embodiment 1
[0081] Regarding the optimization of the benchmark problem NACA-0012 airfoil, the optimization problem is in the inviscid free flow, the Mach number is 0.85 Ma, and the flight state of 0° angle of attack is the optimization of the resistance minimization, and the thickness of the airfoil is constrained. The optimization problem is expressed as follows:
[0082] minimize C D
[0083]
[0084] Among them, C D is the drag coefficient, y is the geometric thickness of the optimized airfoil, y baseline is the geometric thickness of the initial airfoil, x is the abscissa;
[0085] The optimization object NACA-0012 airfoil is defined as follows:
[0086]
[0087] About the model:
[0088] According to the requirements of the optimization problem, the inviscid flow model is adopted. In this case, the viscosity is not considered, and the airfoil resistance is all from the pressure difference resistance, and the viscous resistance is 0.
[0089] Regarding boundary conditions: ...
Embodiment 2
[0111] Regarding the optimization of the shape of the fairing, the basic shape of this example is the fairing. The optimization problem is a drag minimization optimization at a height of 10.1 km and a speed of Mach 1.8 under volume and heat flux constraints. Specifically, the constraints are that the volume of the optimized shape is not smaller than the volume of the basic shape, and the maximum heat flow on the surface is not greater than the maximum heat flow on the surface of the baseline. In summary,
[0112] The optimization problem is formulated as follows:
[0113] minimize C D
[0114] subject to: F≤F baseline
[0115] V≥V baseline
[0116] Among them, F is the maximum heat flux density on the surface of the fairing, V is the volume of the fairing, and F baseline is the maximum heat flux density on the fairing surface of the base airfoil, V baseline is the fairing volume of the base airfoil;
[0117] About the model: In this example, the Spalart-Allmaras (S-A...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com