Information recommendation method and system considering compactness of social network user group
A technology for social network and information recommendation, applied in the field of social network mining, can solve the problems of high time consumption, large breadth-first traversal strategy search range, and difficulty in sharing and utilization of calculation results, so as to save costs and improve experience.
Pending Publication Date: 2021-01-15
YANTAI UNIV +1
7 Cites 2 Cited by
AI-Extracted Technical Summary
Problems solved by technology
[0007] (2) The entire calculation process is executed sequentially. When the number of vertices in the set V is large, it takes a lot of time
[0008] (3) When traversing the graph starting from each vertex in the set S, there are a lot of repeated calculations, and it is difficult to realize the shared utilization of existing calculation results
[0009] (4) Although some existing work uses a bidirectional breadth-first traversal strategy to calculate the shortest route between two points, it needs to maintain a large number of routes and the search range of the breadth-first travers...
Abstract
The invention discloses an information recommendation method and system considering the compactness of a social network user group. The method comprises the steps of obtaining all users in a to-be-analyzed user group in a social network; constructing a graph structure according to all users in the to-be-analyzed user group; regarding each user as a vertex of the graph structure, if friend relationships or attention relationships exist among the users, indicating that correspondingly connected edges exist among the vertexes corresponding to the users, and regarding the interaction times among the users as the weights of the edges; obtaining a vertex set based on the graph structure, and querying the shortest distance between any two vertexes in the vertex set; performing weighted summationon the shortest distance between any two vertexes to obtain the relationship closeness of the to-be-analyzed user group; judging whether the relationship closeness of the to-be-analyzed user group isgreater than a set threshold value or not, and if so, performing information recommendation on each user in the to-be-analyzed user group, namely recommending commodities or services preferred by other users in the to-be-analyzed user group to the current user; otherwise, not recommending the information.
Application Domain
Digital data information retrievalSpecial data processing applications
Technology Topic
User groupComputer network +4
Image
Examples
- Experimental program(4)
Example Embodiment
[0042] Example 1
[0043] This embodiment provides an information recommendation method that considers the closeness of a social network user group;
[0044] Information recommendation methods that consider the closeness of social network user groups, including:
[0045] S101: Obtain all users in the user group to be analyzed in the social network;
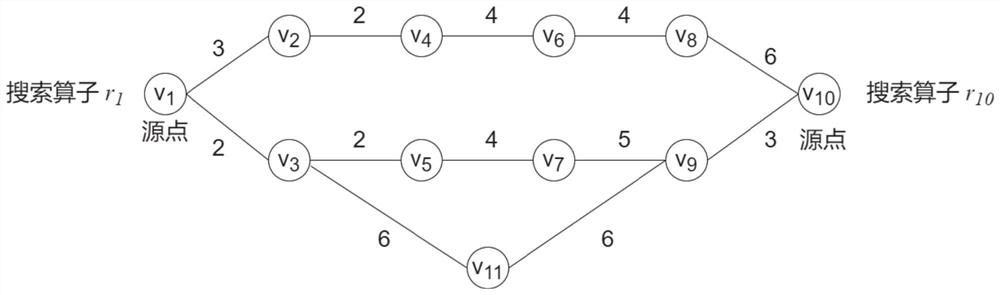
[0046] S102: Construct a graph structure according to all users in the user group to be analyzed; that is, consider each user as a vertex of the graph structure, and if there is a friend relationship or a following relationship between the users, it means that there is a relationship between the vertices corresponding to the users. There are corresponding connected edges, and the number of interactions between users is regarded as the weight of the edge;
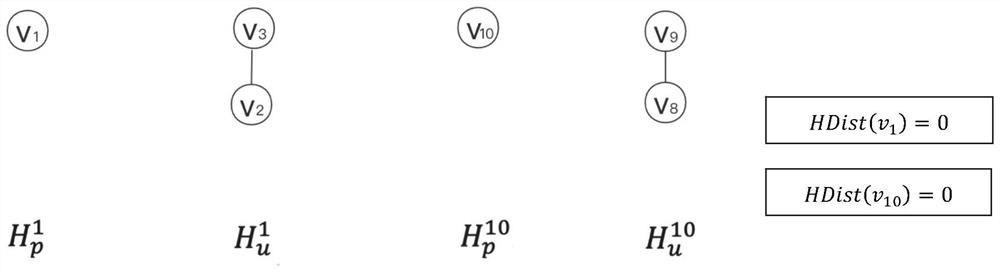
[0047] S103: Based on the graph structure, obtain a vertex set, and query the shortest distance between any two vertices in the vertex set;
[0048]S104: Weighted summation of the shortest distances between any two vertices to obtain the relationship tightness of the user group to be analyzed;
[0049] Determine whether the closeness of the relationship of the user group to be analyzed is greater than the set threshold, and if so, recommend information for each user in the user group to be analyzed, that is, recommend products or services that other users in the user group to be analyzed like to the current user; If not, no information recommendation is made.
[0050] It should be understood that, in the user relationship matrix, if there is a friend relationship or a follow relationship between two users, the value between the two users is 1, otherwise it is 0.
[0051] As one or more embodiments, the S103: based on the graph structure, obtain a vertex set, and query the shortest distance between any two vertices in the vertex set; the specific steps include:
[0052] S1031: Put each vertex v in the vertex set V i as a source point, create a search operator v for it i;
[0053] S1032: Search operator v i Initialize the source point v i The distance to all other vertices in the graph structure G, the source point v i to any vertex v l The distance is written as Dist(v i , v l );
[0054] S1033: Search operator v i Take the source point v i Traverse the graph structure G for the starting point, calculate and update the source point v i The theoretically reachable shortest distance of , the source point v i The theoretically reachable shortest distance is recorded as HDist(v i );
[0055] S1034: Any two search operators r i and r j , and calculate the source point v in parallel according to the theoretically reachable shortest distance of the respective source points i and v j the shortest distance between;
[0056] S1035: Search operator v i Calculate the source point v i After reaching the shortest distance between all other vertices in the vertex set V, terminate the traversal;
[0057] S1036: When any vertex v in the vertex set V x The search operator r x After the traversal is terminated, end; output the shortest distance between any two vertices in the vertex set.
[0058] Further, S1031: convert each vertex v in the vertex set V i As a source point, create a search operator r for it i; The specific implementation is:
[0059] S10311: for the search operator v i Create a min heap min heap For storage and source point v i The shortest distance of vertices has been determined; min heap According to the shortest distance of each vertex to the source point, determine the position of each vertex in the min-heap; the min-heap Initialize with only source point v i;
[0060] S10312: is the search operator r i Create a min heap min heap Used to store vertices whose shortest distance to the source point has not been determined but whose distance to the source point is not infinite; min heap Determine the position of each vertex in the min-heap based on the current distance of each vertex to the source point, the min-heap initialized to the source point v i set of neighbors.
[0061] Further, S1032: search operator v i Initialize the source point v i The distance to all other vertices in the graph structure G, the source point v i to any vertex v l The distance is written as Dist(v i , v l ); the specific implementation is:
[0062] S10321: Search operator r i the source point v i The distance to itself is set to 0, and v i insert into min heap
[0063] S10322: Search operator v i the source point v i to its adjacent vertex v h The distance is set as the edge e i，h weights, and assign v h insert into min heap
[0064] S10323: Search operator v i the source point v i to vertex v y The distance is set to infinity, denoted as where the vertex v y Refers to the graph structure G except for the source point v i vertices other than itself and its adjacent vertices.
[0065] Further, S1033: search operator v i Take the source point v i Traverse the graph structure G for the starting point, calculate and update the source point v i The theoretically reachable shortest distance of , the source point v i The theoretically reachable shortest distance is recorded as HDist(v i ); the specific implementation is:
[0066] S10331: From min heap Calculate the source point v in i the critical vertex v of b; where, the critical vertex v b refers to the min heap middle and source point v i the vertex with the smallest distance and at least one unprocessed neighbor;
[0067] S10332: Set the critical vertex v b to the source point v i The shortest distance of is set to the source point v i The theoretically reachable shortest distance HDist(v i ).
[0068] Further, the S10331: from the min heap Calculate the source point v in i the critical vertex v of b; The specific implementation methods include:
[0069] S103311: Search operator r i take min heap vertex v at the top of the heap f , at this time, the source point v i with v f The current distance of is equal to v i with v f the shortest distance between. search operator r i put vertex v f add to min heap
[0070] S103312: Update source point v i to vertex v f Every adjacent point v of g the distance.
[0071] S103313: Traverse min heap if All neighbors of a vertex in the then mark the vertex as "processed"; if There is at least one adjacency to a vertex in then mark the vertex as "unprocessed";
[0072] S103314: Traverse min heap The first visited vertex with a state of "unprocessed" is the source point v i the critical vertex v of b;
[0073] S103315: Repeat S103311-S103314, keep updating source point v i the critical vertex v of b.
[0074] Further, the specific steps of the S103312 are:
[0075] S1033121: When Dist(v i , v g )=∞, let Dist(v i , v g )=Dist(v i , v f )+Dist(v f , v g ), the vertex v g insert min heap
[0076] S1033122: When Dist(v i , v g )≠∞, if Dist(v i , v g )>Dist(v i , v f )+Dist(v f , v g ), then Dist(v i , v g )=Dist(v i , v f )+Dist(v f , v g ), starting from the min-heap delete vertex v g , and according to the updated Dist(v i , v g ) will be the vertex v g reinsert min heap
[0077] Further, the S1034: any two search operators r i and r j , and calculate the source point v in parallel according to the theoretically reachable shortest distance of the respective source points i and v j The shortest distance between; the specific implementation method is:
[0078] S10341: Search operator v i and r j , respectively at the source point v i and v j Traverse the graph G and continuously compute and update the source point v i The "theoretically reachable shortest distance" HDist(v i ) and the source point v j The "theoretically reachable shortest distance" HDist(v j );
[0079] S10342: When the search operator vi Calculate the vertex v c with the source point v i the shortest distance of , and the search operator r j Also calculate the vertex v c with the source point v j When the shortest distance of , then a v i and v j the new route p k ={v i ,...,v c ,...,v j}, Dist(p k ) represents the route p k the distance.
[0080] S10343: Suppose v i and v j The shortest route currently found between is p s , Dist(p s ) represents the route p s the shortest distance of ; if Dist(p k ) s ), then let p s =P k;
[0081] S10344: Compare Dist(p s ) and the source point v i and v j The sum of the "theoretically reachable shortest distance" (HDist(v i )+HDist(v j )); if Dist(p s ) i )+HDist(v j )), then Dist(p s ) is v i and v j the shortest distance between;
[0082] S10345: Repeat steps S10341-S10344 until the agreed conditions of S10344 are satisfied.
[0083] Further, S1035: search operator r i Calculate the source point v i After reaching the shortest distance between all other vertices in the vertex set V, the traversal is terminated; the specific implementation is as follows:
[0084] S10351: Search operator v i Calculate the source point v according to S1034 i to the source point v j (v j ∈V) after the shortest distance, set v j add to set R i;
[0085] S10352: When the set R i is equal to the set V, which means the search operator r i The source point v has been calculated i The shortest distance to all vertices in the set V, search operator r i Stop traversing.
[0086] In a typical embodiment of the present application, the figure 1 The graph G shown and V={v 1 , v 10} As an example, the vertex v in the graph G is calculated in reverse parallel 1 and v 10 methods for the shortest distance between:
[0087] Step (1) put the vertex v 1 and v 10 As source points, create search operators r for them respectively 1 and r 10;
[0088] Step (2) Search operator r 1 and r 10 Initialize the source points v separately 1 and v 10 the distance to all other vertices in the graph G;
[0089] Step (3) Search operator r 1 and r 10 respectively by the source point v 1 and v 10 Traverse the graph G for the starting point, calculate and update the source point v 1 and v 10 The "theoretically reachable shortest distance";
[0090] Step (4) Search operator r 1 and r 10 The source points v are calculated in parallel according to the "theoretically reachable shortest distance" of the respective source points 1 and v 10 the shortest distance between;
[0091] Step (5) Search operator r 1 and r 10 Calculate the source point v 1 to v 10 After the shortest distance of , terminate the traversal;
[0092] Exemplarily, the step (1) is the vertex v in the set V 1 to v 10 Create search operators r separately 1 and r 10 The way is:
[0093] Step (1.1) is the search operator r 1 Create a min heap For storage and source point v 1 The shortest distance of vertices has been determined. min heap Determine the position of each vertex in the min-heap based on the shortest distance from each vertex to the source. min heap The initialization contains only the source point v 1. Similarly, for the search operator r 10 Create a min heap Initialization and like figure 2 shown;
[0094] Step (1.2) is the search operator r 1 Create a min heap Used to store vertices whose shortest distance from the source point has not been determined but whose distance to the source point is not infinite. min heap Determines each vertex's position in the min-heap based on its current distance from the source. min heap initialized to the source point v 1 set of neighbors. Similarly, for the search operator r 10 Create a min heap Initialization and like figure 2 shown.
[0095] Exemplarily, to search for operator r 1 For example, the step (2) searches for the operator r 1 Initialize the source point v 1 The steps for distances to other vertices in graph G are:
[0096] Step (2.1) Search operator r 1 the source point v 1 The distance to itself is set to 0, and v 1 insert into min heap
[0097] Step (2.2) Search operator r 1 the source point v 1 to its neighbor v 2 and v 3 The distance is set as the edge e 1，2 and e 1，3 weights, and assign v 2 and v 3 insert into min heap
[0098] Step (2.3) Search operator r 1 the source point v 1 The distance to other vertices except itself and its neighbors is set to infinity, denoted as ∞. source point v 1 The distance to all vertices in the graph is as image 3 shown.
[0099] Exemplarily, the step (3) searches for the operator r 1 Take the source point v 1 Traverse the graph G for the starting point, calculate and update the source point v 1 The "theoretical reachable distance" (HDist(v 1 )) steps are:
[0100] Step (3.1) from the min heap Calculate the source point v in 1 The boundary vertex v of b. Here, the boundary vertex v b refers to the min heap middle and source point v 1 the vertex with the smallest distance and at least one unprocessed neighbor;
[0101] Step (3.2) converts the boundary vertex v b to the source point v 1 The shortest distance of is set to the source point v 1 The "theoretically reachable shortest distance" (HDist(v 1 )).
[0102] Exemplarily, the step (3.1) calculates the source point v 1 The boundary vertex v of b The steps are:
[0103] Step (3.1.1) Search operator r 1 take min heap vertex v at the top of the heap f , at this time, the source point v 1 with v f The current distance of is equal to v 1 with v f the shortest distance between. search operator r 1 put vertex v f add to min heap
[0104] Step (3.1.2) update source point v 1 to vertex v f Every adjacent point v of g the distance;
[0105] Exemplarily, the specific steps of the step (3.1.2) are:
[0106] Step (3.1.2.1) when Dist(v 1 , v g )=∞, let Dist(v 1 , v g )=Dist(v 1 , v f )+Dist(v f , v g ), the vertex v g insert min heap;
[0107] Step (3.1.2.2) when Dist(v 1 , v g )≠∞, if Dist(v 1 , v g )>Dist(v 1 , v f )+Dist(v f , v g), then Dist(v 1 , v g )=Dist(v 1 , v f )+Dist(v f , v g ), starting from the min-heap delete vertex v g , and according to the updated Dist(v 1 , v g ) will be the vertex v g reinsert min heap
[0108] Step (3.1.3) Traverse the min heap if All neighbors of a vertex in the then mark the vertex as "processed"; if There is at least one adjacency to a vertex in then marks the vertex as "unprocessed".
[0109] Step (3.1.4) Traverse the min heap , the first visited state is "unprocessed" vertex is the source point v 1 the critical vertex v of b;
[0110] Step (3.1.5) Repeat steps (3.1.1)-(3.1.4) to continuously update the source point v 1 the critical vertex v of b.
[0111] like figure 2 shown, when initializing, The vertex at the top of the middle heap is v 3 , v 3 The adjacent point of is v 5 and v 11. search operator r 1 According to steps (3.1) and (3.2) for vertices v 3 After processing, the min heap and like Figure 4 shown. At this time, since the source point still has an adjacent point v 2 belong so v 1 and v 3 are all "unprocessed", then v 1 The boundary point of is itself, HDist(v 1 )=0.
[0112] Figure 4 , Image 6 , Figure 8 , Figure 10 , Figure 12 , Figure 14 The search operator r is given respectively 1 Process v in turn 2 , v 5 , v 4 , v 7 , v 11 , v 6 min heap and The state change of and the source point v 1 The "theoretically reachable shortest distance" (HDist(v 1 )) update. At the same time, the search operator r is also given 10 Process v in turn 9 , v 8 , v 7 , v 11 , v 6 , v 5 , v 4 min heap and The state change of and the source point v 10 The "theoretically reachable shortest distance" (HDist(v 10 )) update.
[0113] Exemplarily, the step (4) searches for the operator r 1 and r 10 Calculate v in parallel based on the "theoretically reachable shortest distance" from the respective source points 1 and v 10 The steps for the shortest distance between:
[0114] Step (4.1) Search operator r 1 and r 10 According to step (3), the source point v is 1 and v 10 Traverse the graph G and continuously compute and update the source point v 1 The "theoretically reachable shortest distance" (HDist(v 1 )) and the source point v 10 The "theoretically reachable shortest distance" (HDist(v 10 ));
[0115] Step (4.2) When the search operator r 1 Calculate the vertex v c with the source point v 1 the shortest distance of , and the search operator r 10 Also calculate the vertex v c with the source point v 10 When the shortest distance of , then a v 1 and v 10 the new route p k ={v 1 ,...,v c ,...,v 10}, Dist(p k ) represents the route p k the distance.
[0116] Step (4.3) Suppose v 1 and v 10 The shortest route currently found between is p s , Dist(p s ) represents the route p s the shortest distance. If Dist(p k ) s ), then let p s =p k;
[0117] Step (4.4) compares Dist(p s ) and the source point v 1 and v 10 The sum of the "theoretically reachable shortest distance" (HDist(v 1 )+HDist(v 10 )). If Dist(p s ) 1 )+HDist(v 10 )), then Dist(p s ) is v 1 and v 10 the shortest distance between;
[0118] Step (4.5) Repeat steps 4.1-4.4 until the agreed conditions of step (4.4) are met.
[0119] like Figure 1-Figure 17 As shown, when the search operator r 1 calculate v 1 to v 7 When the shortest distance of , produces a v 1 and v 10 the route p 1 ={v 1 , v 3 , v 5 , v 7 , v 9 , v 10}, Dist(p 1 ) = 16, p S =p 1.
[0120] At this point, HDist(v 1 )=2, HDist(v 10 )=8, since 2+8<16, continue to traverse.
[0121] When the search operator r 1 calculate v 1 to v 11 When the shortest distance of , produces a v 1 and v 11 the route p 2 ={v 1 , v 3 , v 11 , v 9 , v 10}, Dist(p 2 ) = 17, Dist(p s ) 2 ).
[0122] At this point, HDist(v 1 )=5, HDist(v 10 )=9, since 5+9 s ), continue to traverse;
[0123] When the search operator r 1 calculate v 1 to v 6 When the shortest distance of , produces a v 1 and v 10 the route p 3 ={v 1 , v 2 , v4, v 6 , v 8 , v 10}, Dist(p 3 )=19, Dist(ps) 3 ).
[0124] At this point, HDist(v 1 )=8, HDist(v 10 )=9, 9+8>Dist(ps), it can be obtained that Dist(ps)=16 is v 1 and v 10 The shortest distance between the search operator r 1 and r 10 Stop traversing.
[0125] like figure 2 and image 3 shown, initialization steps; such as Figure 4 and Figure 5 As shown, the search operator r 1 handle v 3 , the search operator r 10 handle v 9;like Image 6 and Figure 7 As shown, the search operator r 1 handle v 2 , the search operator r 10 handle v 8;like Figure 8 and Figure 9 As shown, the search operator r 1 handle v 5 , the search operator r 10 handle v 7;like Figure 10 and Figure 11 As shown, the search operator r 1 handle v 4 , the search operator r 10 handle v 11;like Figure 12 and Figure 13 As shown, the search operator r 1 handle v 7 , the search operator r 10handle v 6;like Figure 14 and Figure 15 As shown, the search operator r 1 handle v 11 , the search operator r 10 handle v 5;like Figure 16 and Figure 17 As shown, the search operator r 1 handle v 6 , the search operator r 10 handle v 4.
Example Embodiment
[0126] Embodiment 2
[0127] This embodiment provides an information recommendation system that considers the closeness of social network user groups;
[0128] Information recommendation systems considering the closeness of social network user groups, including:
[0129] an acquisition module, which is configured to: acquire all users in the user group to be analyzed in the social network;
[0130] The graph structure component module is configured to: construct a graph structure according to all users in the user group to be analyzed; that is, consider each user as a vertex of the graph structure, if there is a friend relationship or a follower relationship between users, then Indicates that there are correspondingly connected edges between the vertices corresponding to the user, and the number of interactions between users is regarded as the weight of the edge;
[0131] a query module, which is configured to: obtain a vertex set based on the graph structure, and query the shortest distance between any two vertices in the vertex set;
[0132] A recommendation module, which is configured to: weight the sum of the shortest distances between any two vertices to obtain the closeness of the relationship of the user group to be analyzed;
[0133] Determine whether the closeness of the relationship of the user group to be analyzed is greater than the set threshold, and if so, recommend information for each user in the user group to be analyzed, that is, recommend products or services that other users in the user group to be analyzed like to the current user; If not, no information recommendation is made.
[0134] It should be noted here that the above acquisition module, graph structure component module, query module and recommendation module correspond to steps S101 to S104 in Embodiment 1, and the examples and application scenarios implemented by the above modules and the corresponding steps are the same, but not the same. It is limited to the content disclosed in the first embodiment above. It should be noted that the above modules may be executed in a computer system such as a set of computer-executable instructions as part of the system.
[0135] The description of each embodiment in the foregoing embodiments has its own emphasis. For the part that is not described in detail in a certain embodiment, reference may be made to the relevant description of other embodiments.
[0136] The proposed system can be implemented in other ways. For example, the system embodiments described above are only illustrative. For example, the division of the above modules is only a logical function division. In actual implementation, there may be other division methods. For example, multiple modules may be combined or integrated into other A system, or some feature, can be ignored, or not implemented.
Example Embodiment
[0137] Embodiment 3
[0138] This embodiment also provides an electronic device, including: one or more processors, one or more memories, and one or more computer programs; wherein the processor is connected to the memory, and the one or more computer programs are Stored in the memory, when the electronic device runs, the processor executes one or more computer programs stored in the memory, so that the electronic device executes the method described in the first embodiment.
[0139] It should be understood that, in this embodiment, the processor may be a central processing unit (CPU), and the processor may also be other general-purpose processors, digital signal processors, DSPs, application-specific integrated circuits (ASICs), off-the-shelf programmable gate arrays (FPGAs), or other programmable logic devices. , discrete gate or transistor logic devices, discrete hardware components, etc. A general purpose processor may be a microprocessor or the processor may be any conventional processor or the like.
[0140] The memory may include read-only memory and random access memory and provide instructions and data to the processor, and a portion of the memory may also include non-volatile random access memory. For example, the memory may also store device type information.
[0141] In the implementation process, each step of the above-mentioned method can be completed by a hardware integrated logic circuit in a processor or an instruction in the form of software.
[0142] The method in the first embodiment can be directly embodied as being executed by a hardware processor, or executed by a combination of hardware and software modules in the processor. The software modules may be located in random access memory, flash memory, read-only memory, programmable read-only memory or electrically erasable programmable memory, registers and other storage media mature in the art. The storage medium is located in the memory, and the processor reads the information in the memory, and completes the steps of the above method in combination with its hardware. To avoid repetition, detailed description is omitted here.
[0143] Those skilled in the art can realize that the units and algorithm steps of each example described in conjunction with this embodiment can be implemented by electronic hardware or a combination of computer software and electronic hardware. Whether these functions are performed in hardware or software depends on the specific application and design constraints of the technical solution. Skilled artisans may implement the described functionality using different methods for each particular application, but such implementations should not be considered beyond the scope of this application.
PUM
Description & Claims & Application Information
We can also present the details of the Description, Claims and Application information to help users get a comprehensive understanding of the technical details of the patent, such as background art, summary of invention, brief description of drawings, description of embodiments, and other original content. On the other hand, users can also determine the specific scope of protection of the technology through the list of claims; as well as understand the changes in the life cycle of the technology with the presentation of the patent timeline. Login to view more.
Similar technology patents
Apparatus and method for low-density cellular wood plastic composites
Owner:STRANDEX CORP
Preparing method of bamboo fiber winding composite tube
Owner:XINJIANG GUANGSHUI PIPE
Efficient ultrasound system for two-dimensional c-scan imaging and related method thereof
Owner:UNIV OF VIRGINIA ALUMNI PATENTS FOUND
Classification and recommendation of technical efficacy words
- Improve experience
- low cost
Scalable search system using human searchers
Owner:CHACHA SEARCH
Screen projection method, system and related device
Owner:HUAWEI TECH CO LTD
Incoming call processing method and mobile terminal
Owner:ZTE CORP
Systems and methods for interactive gameplay
Owner:KING COM
Smart home controller and communication method thereof
Owner:HUIZHOU TCL MOBILE COMM CO LTD
Method, apparatus and article for microfluidic control via electrowetting, for chemical, biochemical and biological assays and the like
Owner:KECK GRADUATE INST OF APPLIED LIFE SCI
System and method for transmitting wireless digital service signals via power transmission lines
Owner:NEXTEL COMMUNICATIONS
System and method for determination of position
Owner:STEELE CHRISTIAN
Antenna device and method for attaching the same
Owner:NEC CORP