Job shop scheduling optimization method with sufficient necessary condition neighborhood structure

A necessary condition, job shop technology, applied in the field of job shop scheduling optimization, can solve the problems of limited number of neighborhood solutions, long search time, low precision, etc., to improve search quality, improve search efficiency, improve search efficiency and search directional effect

Pending Publication Date: 2021-02-05
HUAZHONG UNIV OF SCI & TECH
View PDF0 Cites 2 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

For JSP, the neighborhood structure based on the critical path is mostly used. The critical path refers to the longest path from the beginning of processing to the end of all workpiece processing. Now there are three commonly used neighborhood structures based on the critical path, which are named N5 , N6, N7, Nowicki et al. (Nowicki, E., & Smutnicki, C. (1996). A fast taboo search algorithm for the job shop problem. Management Science, 42(6), 797-813.) proposed the N5 neighborhood structure , Balas et al. (Balas E, Vazacopoulos

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Job shop scheduling optimization method with sufficient necessary condition neighborhood structure
  • Job shop scheduling optimization method with sufficient necessary condition neighborhood structure
  • Job shop scheduling optimization method with sufficient necessary condition neighborhood structure

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

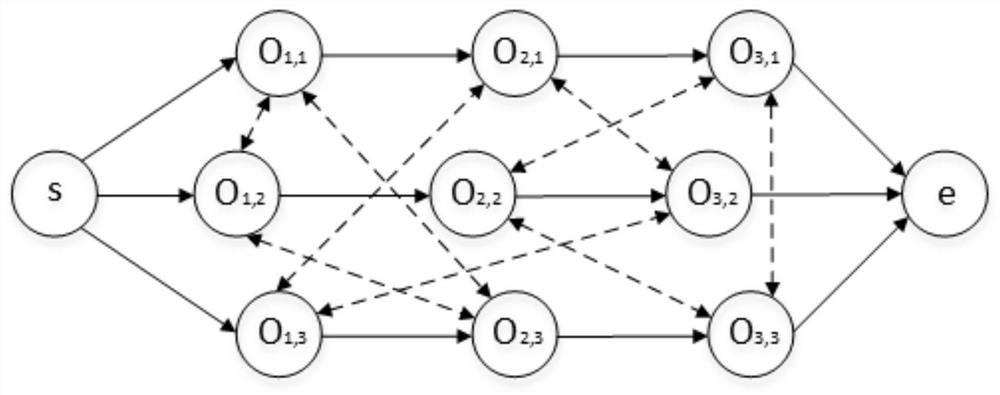
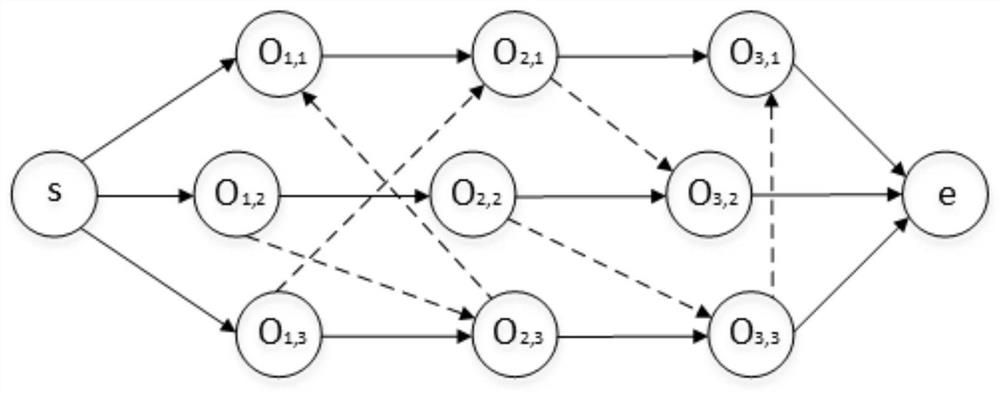
[0057] like Image 6 As shown, process u is the first processing process on the critical path block, and v is the same critical path block as u and the process processed after u. Use horizontal traversal or other methods to check whether there is a path from js(u) to v, if not, then move u to process v to obtain a feasible neighborhood solution, such as Figure 7 shown.

Embodiment 2

[0059] like Figure 8 As shown, process u is the first processing process on the critical path block, and v is the same critical path block as u and the process processed after u. Use horizontal traversal or other methods to check whether there is a path from u to jp(v), if not, move v to be processed before process u to obtain a feasible neighborhood solution, such as Figure 9 shown.

Embodiment 3

[0061] like Figure 10 As shown, process v is the last processing process on the critical path block, and u is the same critical path block as v and the process processed before v. Use horizontal traversal or other methods to check whether there is a path from js(u) to v, if not, then move u to process v to obtain a feasible neighborhood solution, such as Figure 11 shown.

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

PUM

No PUM Login to view more

Abstract

The invention belongs to the technical field related to workshop scheduling, and discloses a job shop scheduling optimization method with a sufficient necessary condition neighborhood structure. The method comprises the following steps: obtaining a scheduled critical path according to a current solution of a job shop scheduling problem, and adjusting the processing sequence of procedures in a critical path block according to sufficient necessary conditions to obtain multiple different processing sequences; and calculating the total processing time of each processing sequence, and taking the processing sequence with the shortest total processing time as the current scheduling sequence. The sufficient necessary conditions are as follows: (1) a path from js (u) to v does not exist, and a neighborhood solution generated by processing after u moves to v is a sufficient necessary condition of a feasible solution; and (2) a path from u to jp (v) does not exist and is a sufficient necessary condition that a neighborhood solution generated by processing before v moves to u is a feasible solution. By means of the invention, when the job shop scheduling problem is solved, the solving qualityis effectively improved, and the solving time is shortened.

Description

[0001] technology neighborhood [0002] The invention belongs to the technical field related to job shop scheduling, and more specifically relates to a job shop scheduling optimization method with a sufficient and necessary condition neighborhood structure. Background technique [0003] The workshop scheduling problem refers to the rational allocation of production resources to improve production efficiency and reduce production costs. The job shop scheduling problem (job-shop scheduling problem, JSP) is a classic shop scheduling problem, which is described as having n workpieces, and each workpiece has m processes that need to be processed on m different machines. The sequence of the machines that flow through during the processing is different, and it is necessary to arrange the processing sequence and processing time of the workpieces on each machine so that certain indicators can be optimized. [0004] JSP is an NP-hard problem. For small-scale problems, exact solutions c...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

Application Information

Patent Timeline
no application Login to view more
IPC IPC(8): G06Q10/06
CPCG06Q10/0631G06Q10/0633
Inventor 李新宇桂林高亮
Owner HUAZHONG UNIV OF SCI & TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Try Eureka
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap