Local eigendimension estimation method based on Gaussian mixture function compression transformation
A technology of intrinsic dimension, compression transformation, applied in computing, complex mathematical operations, computer parts and other directions, can solve the problem of intrinsic dimension jump, can only be estimated, can not estimate the basis vector, etc., to achieve accurate estimated value Effect
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
[0062] Implementation points 1. Taking the two-dimensional sample space as an example, the distribution of samples is as follows: Figure 4 shown.
[0063] Implementation Point 2. Setting Discrete Scale ,coefficient .
[0064] Implementation point 3. Selection of compression transformation function .
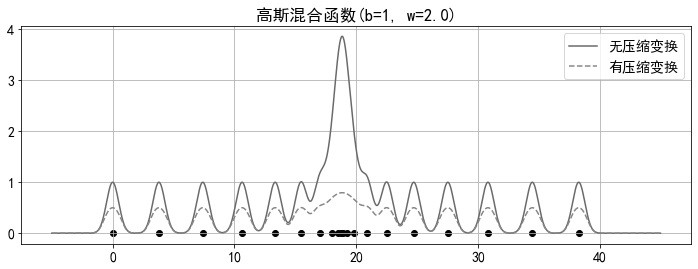
[0065] Implementation point 4. The Gaussian mixture function value of each point in the two-dimensional sample space, and the value after compression transformation, such as Figure 7 shown.
[0066] Implementation Point 5. Selection of Compensation Coefficients .
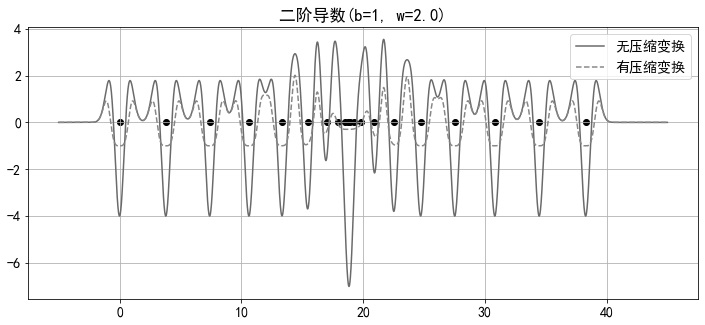
[0067] Implementation Point 6. Two samples for each sample point in two-dimensional space multiplied by the compensation factor After, such as Figure 8Shown by dots in . in addition, Figure 8 The × point in demonstrates the shift of each sample point along the direction of the eigenvector.
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com