Split iteration method for solving kinetic equation of flexible beam system
A technology of system dynamics and system equations, applied in constraint-based CAD, special data processing applications, instruments, etc., can solve problems such as large number of generalized coordinates, ignore boom coupling, reduce solution accuracy, etc., and improve numerical stability , improve solution efficiency and reduce the number of variables
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
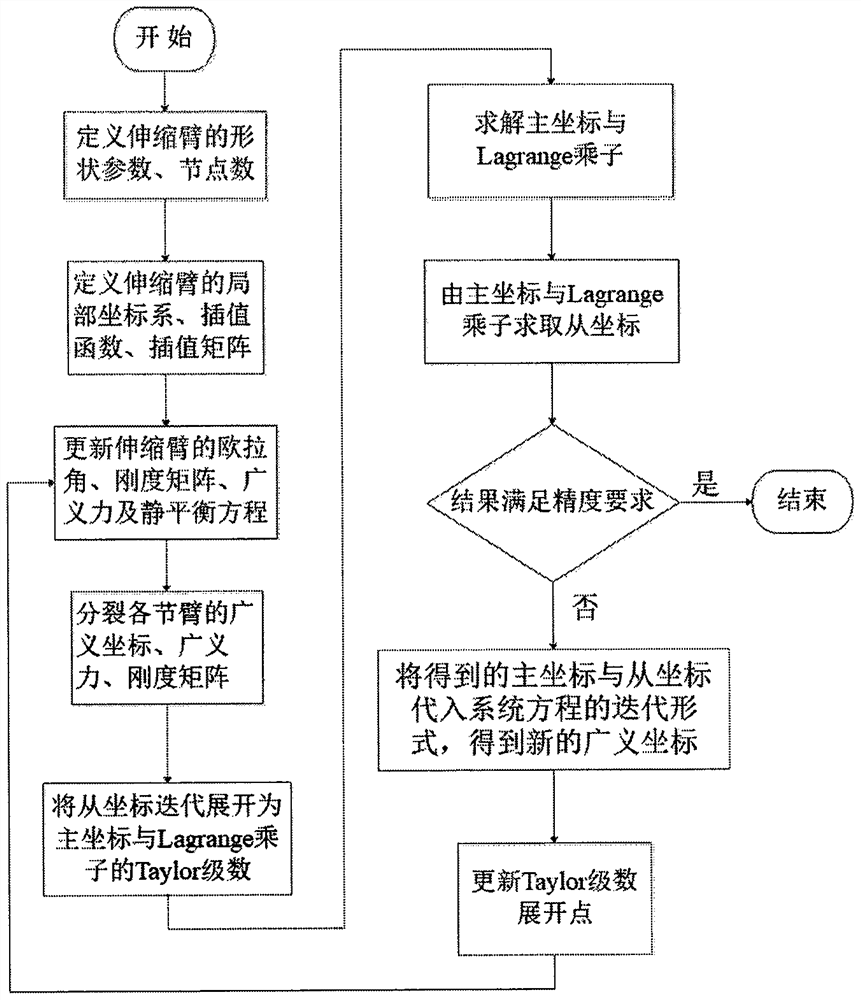
[0060] Further illustrate the content of the present invention below in conjunction with embodiment and accompanying drawing, embodiment adopts ANCF method and generalized alpha method (selected modeling method and numerical integration method are only to illustrate patent content, and this patent is to modeling method and numerical integration method Not limited) Modeling and solving of the working arm mechanism of a certain type of aerial work platform.
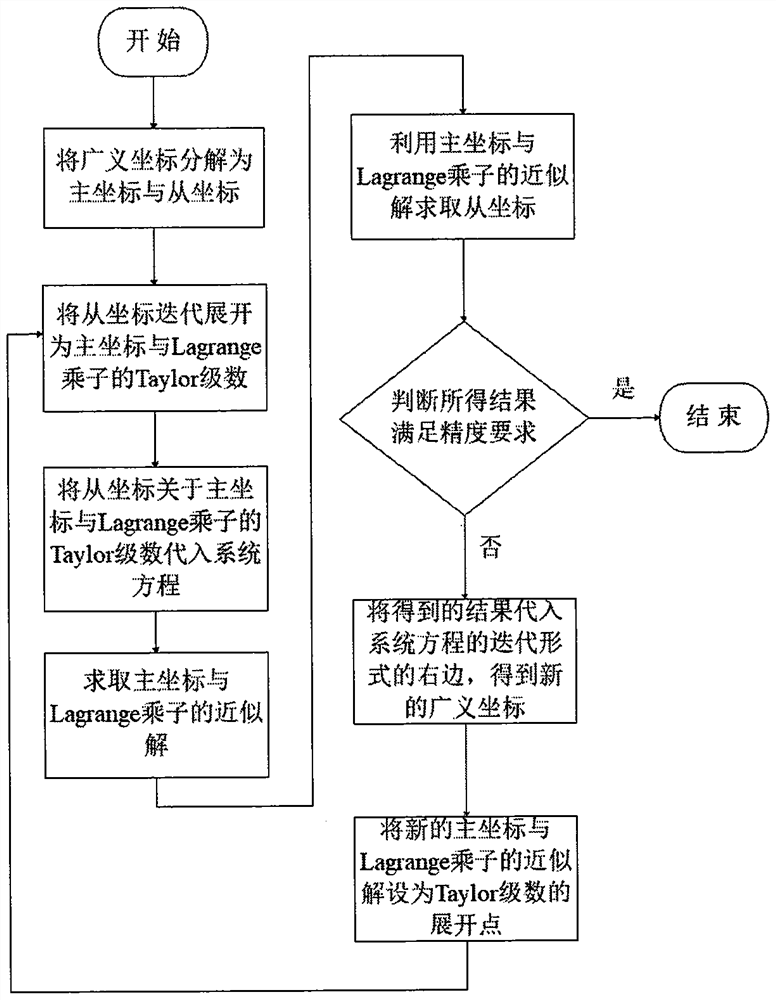
[0061] The static solution method of the telescopic arm mechanism is as follows:
[0062] (1) According to the actual structure of the telescopic arm mechanism, define the shape parameters and grid division of each section arm;
[0063] (2) Establish the local coordinate system, interpolation function, and interpolation matrix of each joint arm;
[0064] (3) Update the Euler angles, stiffness matrix, generalized force and static equilibrium equations of each arm in the telescopic arm mechanism;
[0065] (4) The generalize...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com