Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

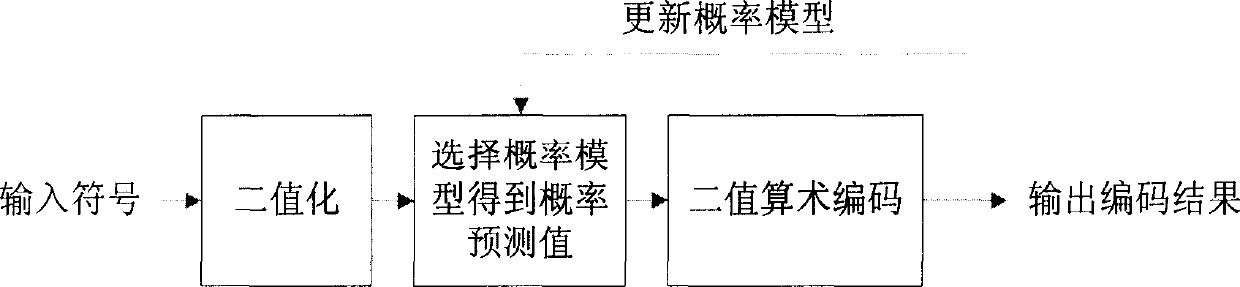
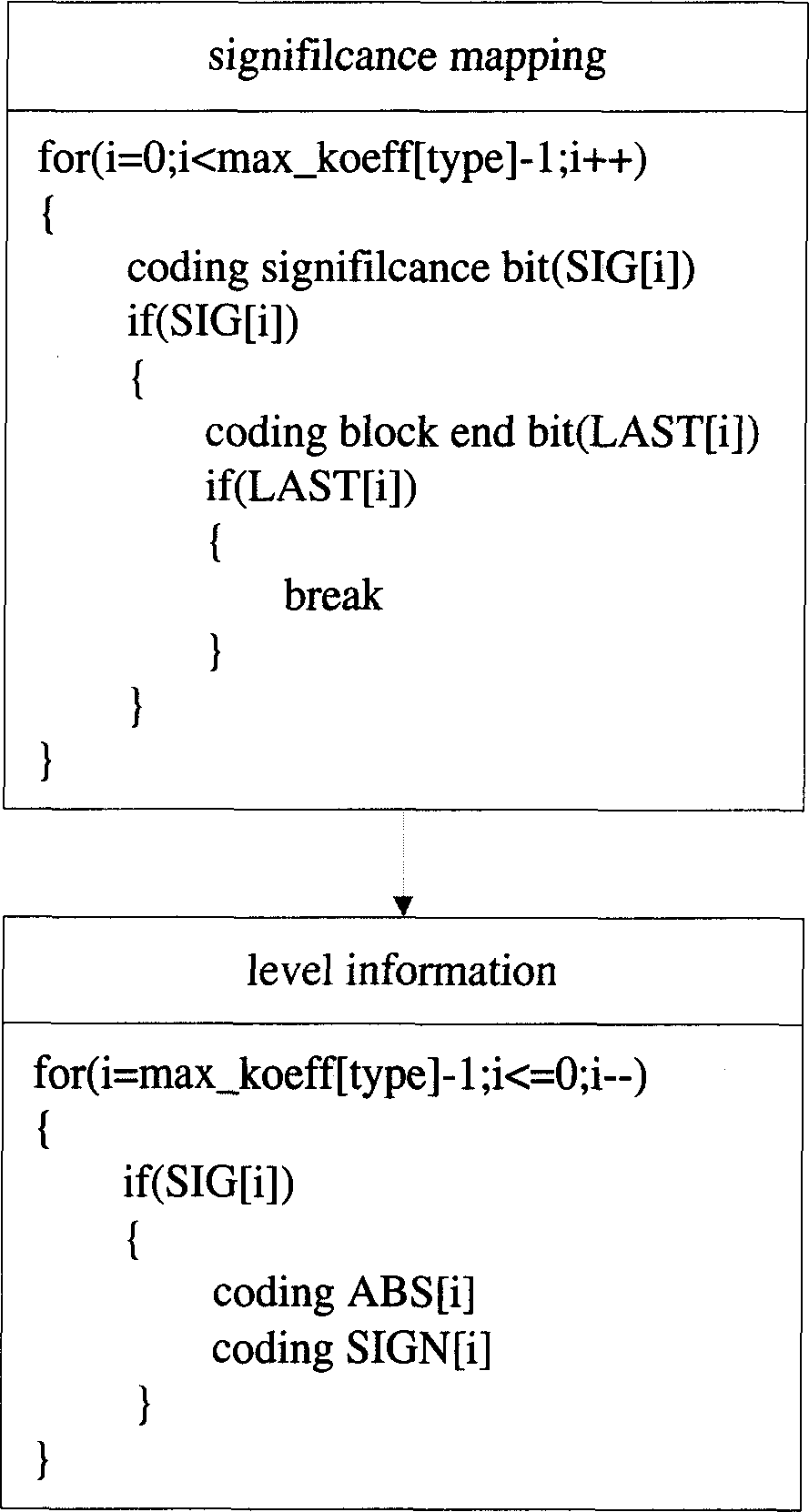
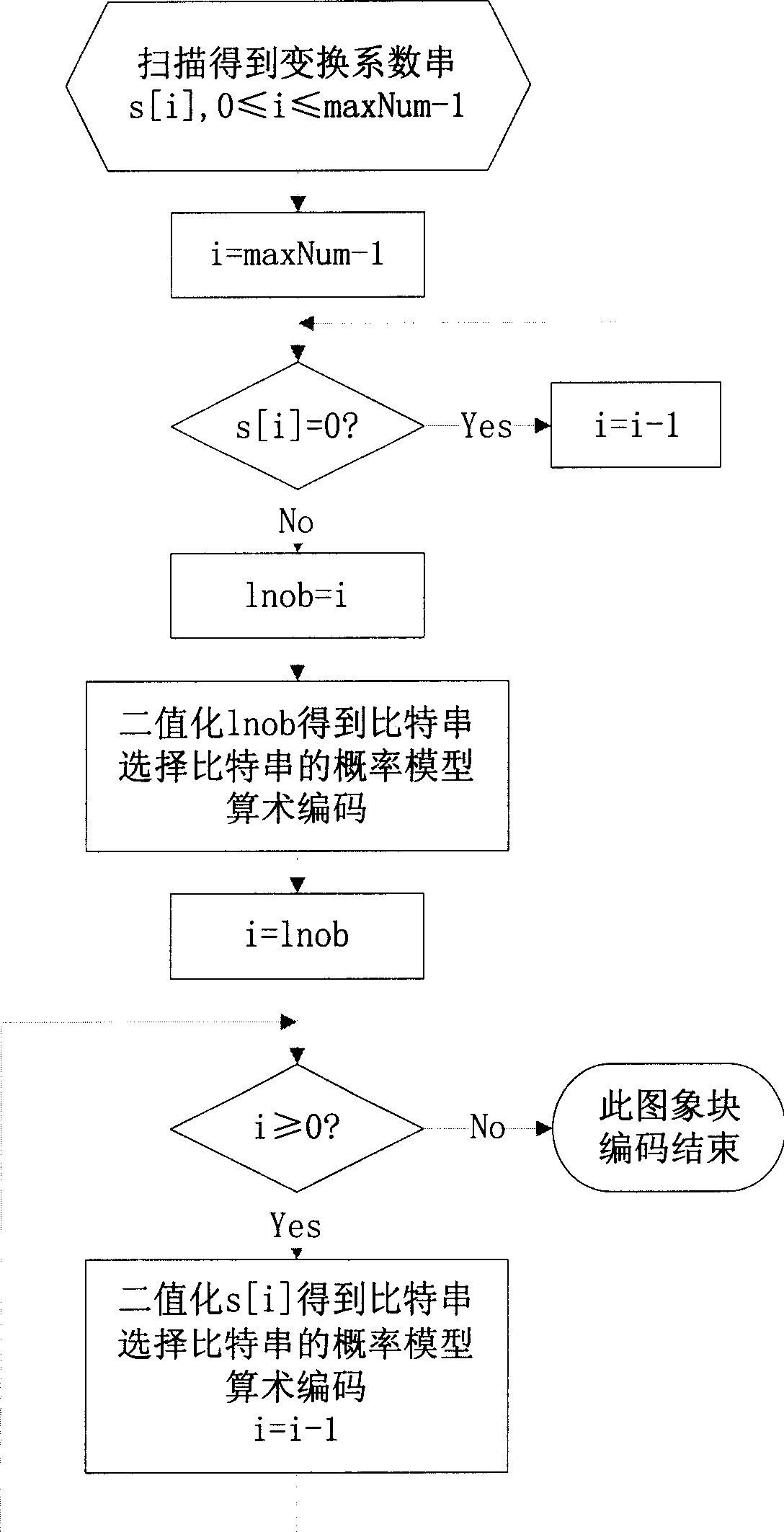
Binary and probability model selecting method for use in image arithmetic code

A probabilistic model and arithmetic coding technology, applied in the field of image coding, can solve the problems of high compression efficiency, slow implementation speed, and high complexity of arithmetic coding

Inactive Publication Date: 2006-01-11
TSINGHUA UNIV
View PDF0 Cites 34 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0010] Due to the high complexity of arithmetic coding and the slow implementation speed, the entropy coding algorithms before the international video coding standard MPEG-2 all used variable-length codes, and did not use arithmetic coding.
[0011] However, arithmetic coding also has the following obvious advantages: the compression efficiency is close to the optimal theoretical value, that is, the entropy of the source, and its compression efficiency is higher than that of variable-length codes; and the coding process and probability modeling process in arithmetic coding are separated, which is easy to do Changes to Adaptive Statistical Properties

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Binary and probability model selecting method for use in image arithmetic code
  • Binary and probability model selecting method for use in image arithmetic code
  • Binary and probability model selecting method for use in image arithmetic code

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0065] Embodiment 1: Binarize the position value of the last non-zero coefficient into 2 layers, ie N=2. The first layer is divided into 8 intervals, namely k 1 =8. The second layer is divided into 8 intervals, namely k 2 =8. The unary code of layer 1 is as follows. Set the initial value of the serial number of the first-level unary code probability model to 0, that is, A 1 =0, the serial number of the probability model used is 0~6, one probability model for each bit, the probability model used is as follows.

[0066] last non-zero

[0067] Table four

[0068] last non-zero

[0069] Table five

[0070] Applying this implementation method to the example in FIG. 4 is specifically as follows: the last non-zero coefficient value 11 is within the interval of 8-15 in the first layer. The intervals from 8 to 15 in the second layer are divided into 8 intervals, the interval length is 1, and 11 is in ...

Embodiment 2

[0073] Embodiment 2: Binarize the position value of the last non-zero coefficient into 6 layers, that is, N=6. Each layer is divided into 2 sections. The unary code for each interval is 0 or 1. At this time, the result of the unary code obtained by binarization is equivalent to the binary value of the position value of the last non-zero coefficient. Set the initial value of the serial number of the first-level unary code probability model to 0, that is, A 1 =0, the serial number of the probability model used is 0. The relationship between the initial value N of the probability model number of the nth layer and the initial value M of the model number of the n-1th layer

[0074] As follows: s is the unary code of the n-1th layer, which is 0 or 1.

[0075] If s=0, N=M×2+1

[0076] Otherwise s=1, N=M×2+2

[0077] Tier 1

layer 2

layer 3

layer 4

layer 5

Layer 6

6 layers of unary code

0

0

1

0

1

1

Probabi...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

This invention relates to a binary-value method in the encoding of conversion coefficient entropy in image encoding, which designs a new binary-valued method to a series of factors after scanning the image block characterizing in first of all, encoding the last non-zero coefficient position information in a code stream then the last non-zero factor begins to carry out algorithm encoding to all factors in countdown sequence secondly, after the last non-zero factor is binary-valued, a probability model is selected to encode it.

Description

technical field [0001] The invention belongs to the field of image coding in signal processing, in particular to a method for binarizing scanned coefficient strings and selecting a probability model in image coding. Background technique [0002] In existing image coding methods, each image of a video image is generally divided into several image blocks, and then each image block is encoded. The so-called image block refers to a set of pixels in an image as the basic unit of encoding, which is a set of pixels with a square, a rectangle or an arbitrary shape boundary whose number of pixels is greater than or equal to 1. The coding steps generally include prediction, transformation, quantization, scanning and entropy coding. There are usually two methods of entropy coding, namely variable length code and arithmetic coding. [0003] The basic idea of ​​arithmetic coding is to encode the source with real numbers in [0,1). The length of the real number is related to the probabi...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): H04N7/50G06T9/00H04N19/13H04N19/149H04N19/91
Inventor 何芸李亨王博
Owner TSINGHUA UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com