Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Time domain parameter blind evaluation method of OFDM (Orthogonal Frequency Division Multiplexing) signals

A time-domain parameter and blind estimation technology, applied in baseband system components, multi-frequency code systems, etc., can solve problems such as unsuitable for wireless channel applications and poor estimation performance, and achieve the effect of reducing computational complexity and improving estimation performance

Inactive Publication Date: 2011-02-16
XIDIAN UNIV
View PDF2 Cites 23 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

This method is based on the detection of the distance between peaks, and the estimation performance is poor under low signal-to-noise ratio and multipath channel conditions
Therefore, the above method is not suitable for application in actual wireless channels

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Time domain parameter blind evaluation method of OFDM (Orthogonal Frequency Division Multiplexing) signals
  • Time domain parameter blind evaluation method of OFDM (Orthogonal Frequency Division Multiplexing) signals
  • Time domain parameter blind evaluation method of OFDM (Orthogonal Frequency Division Multiplexing) signals

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

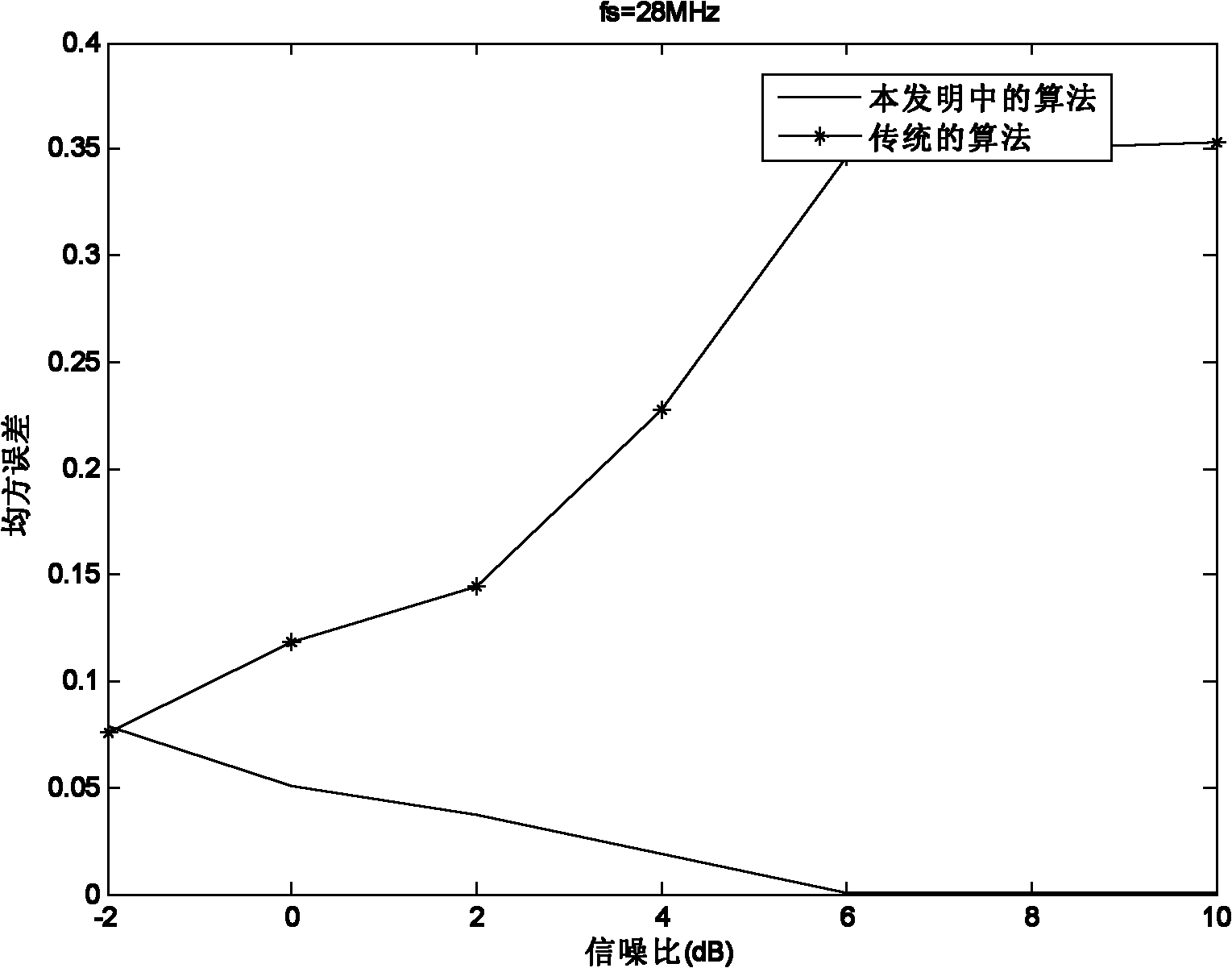
[0030] The OFDM signal used in the present invention is a DVB-T OFDM signal 2K FFT mode, and the multipath channel is a GSM TU 6-path channel model.

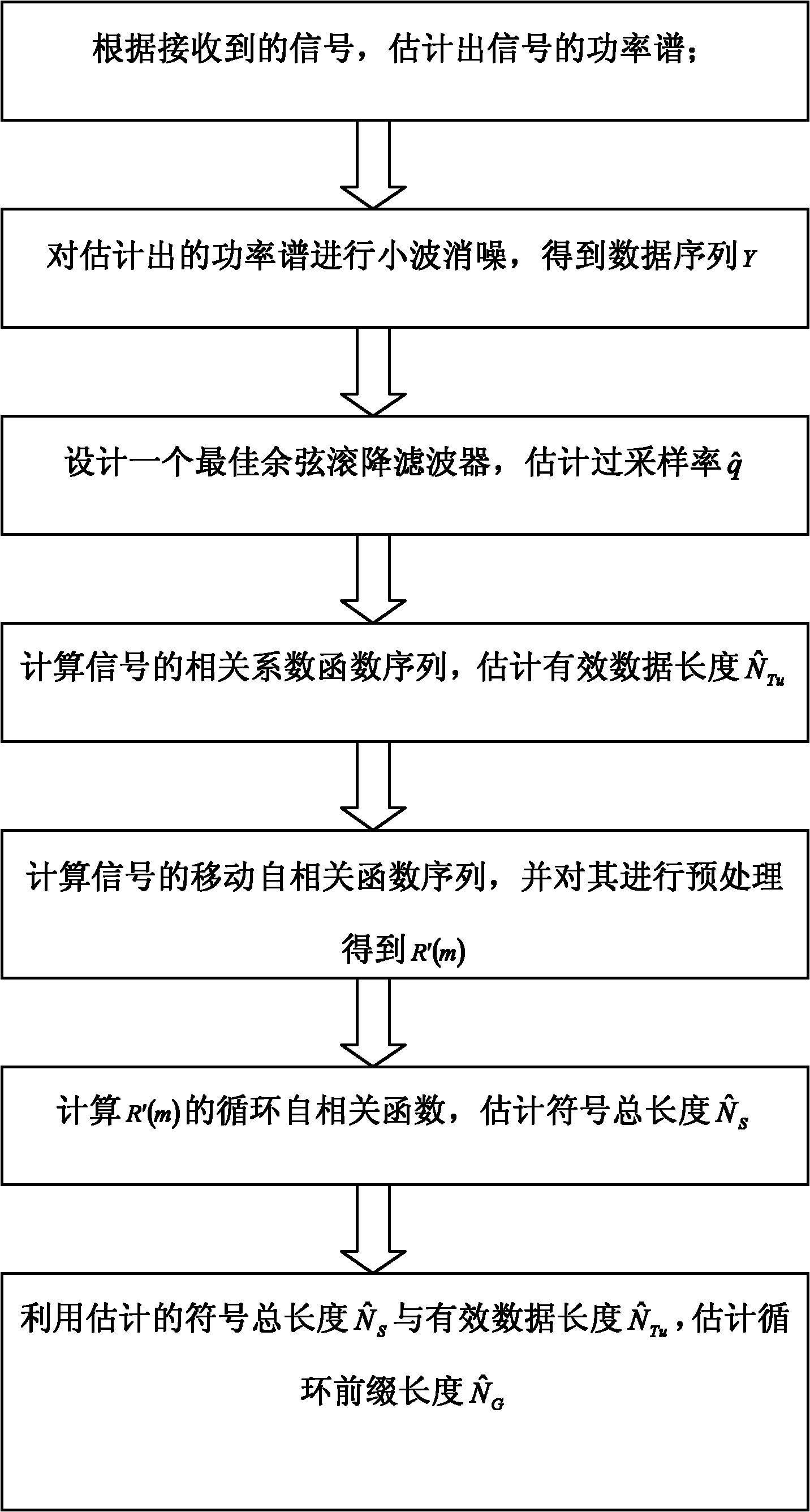
[0031] refer to figure 1 , the specific implementation steps of the present invention are as follows:

[0032] Step 1, utilize Welch method to estimate the power spectrum of OFDM baseband oversampling signal r (i), wherein i=1, 2, Λ, N, N is the data length of interception:

[0033] 1.1) Divide the intercepted OFDM baseband oversampling signal r(i) into L segments, each segment data length M L , the OFDM baseband oversampling signal data in the first section can be expressed as:

[0034] r l (k')=r(k'+(l-1)·M L ), k'=1, 2, ΛM L , l=1, 2, Λ, L 1)

[0035] in l represents a data segment variable, k' represents a data symbol variable;

[0036] 1.2) Add the window function w(k′) to each segment of data to obtain the corrected periodogram of each segment, and the corrected periodogram of the first segment is expressed as:

...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a time domain parameter blind evaluation method of OFDM (Orthogonal Frequency Division Multiplexing) signals, which mainly solves the problems of poor evaluation performance and high calculation load of the traditional evaluation method under the conditions of low signal to noise ratio and multipath channels. The evaluation method comprise the steps of: designing a power spectrum of an approaching signal of an optimum cosine roll-off filter, and evaluating an oversampling rate; a calculating correlation coefficient function sequence of an OFDM baseband sampling signal,and evaluating an effective data length; calculating a cycle autocorrelation function of a signal moving autocorrelation function sequence, searching a cycle frequency corresponding to a peak value position of the cycle autocorrelation function, and evaluating a total symbol length; and evaluating a cycle prefix length by utilizing the evaluated total symbol length and the evaluated effective data length. The invention can ensure that the evaluation error of the oversampling rate and the total symbol length is small, the accuracy rate of the evaluation of the effective data length is high, and the performance of the evaluation of the total symbol length is free of the influence of frequency shift and phase shift, and the method can be used for the time domain parameter blind evaluation ofthe OFDM baseband sampling signals in the communication technical field.

Description

technical field [0001] The invention belongs to the technical field of communication, and specifically relates to a method for blindly estimating time-domain parameters of OFDM signals under the conditions of multipath channels and low signal-to-noise ratios, which can be used for the oversampling rate, effective data length, total symbol length and cycle of OFDM signals. An estimate of the prefix length. Background technique [0002] Orthogonal Frequency Division Multiplexing (OFDM) technology has been widely used in many fields because of its good anti-frequency selective fading characteristics, and has become the key transmission technology of the fourth generation mobile communication system in the future. At the same time, the estimation and detection of modulation parameters of OFDM signals are becoming increasingly prominent. In non-cooperative communication systems, to realize timing sequence reconstruction and demodulation of fully blind OFDM signals, it is first ne...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): H04L27/26H04L25/02
Inventor 李兵兵刘明骞唐宁洁
Owner XIDIAN UNIV
Features
  • Generate Ideas
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com