Multi-measuring-point planeness evaluation method based on support vector classification

A technology of support vector classification and support vector machine, which is applied in the direction of measuring devices and instruments, can solve the problems of complex calculation, falling into local optimum, and difficult to guarantee the accuracy of evaluation, so as to improve calculation efficiency, improve accuracy and reduce calculation The effect of data volume

Active Publication Date: 2012-06-20
SOUTH CHINA UNIV OF TECH
View PDF2 Cites 12 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

The calculation speed of the least square method is faster, but it is difficult to guarantee the evaluation accuracy by using the least square plane instead of the minimum area plane; the calculation accuracy of the search method is high, but

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Multi-measuring-point planeness evaluation method based on support vector classification
  • Multi-measuring-point planeness evaluation method based on support vector classification
  • Multi-measuring-point planeness evaluation method based on support vector classification

Examples

Experimental program
Comparison scheme
Effect test

Example Embodiment

[0016] In order to make the objectives, technical solutions and advantages of the present invention clearer, the following will further describe the embodiments of the present invention in detail with reference to the accompanying drawings:

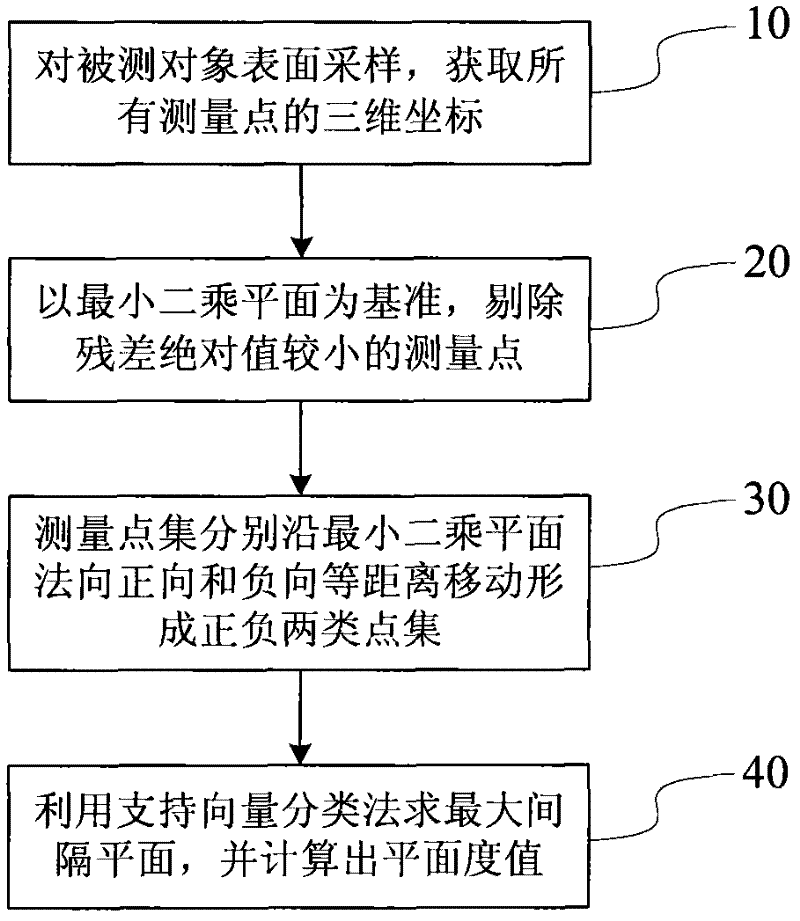
[0017] See figure 1 , Is a flowchart of a method for multi-point flatness evaluation based on support vector classification, the method includes the following steps:

[0018] Step 10: Sample the points on the measured surface to obtain the three-dimensional coordinates of all the measured points.

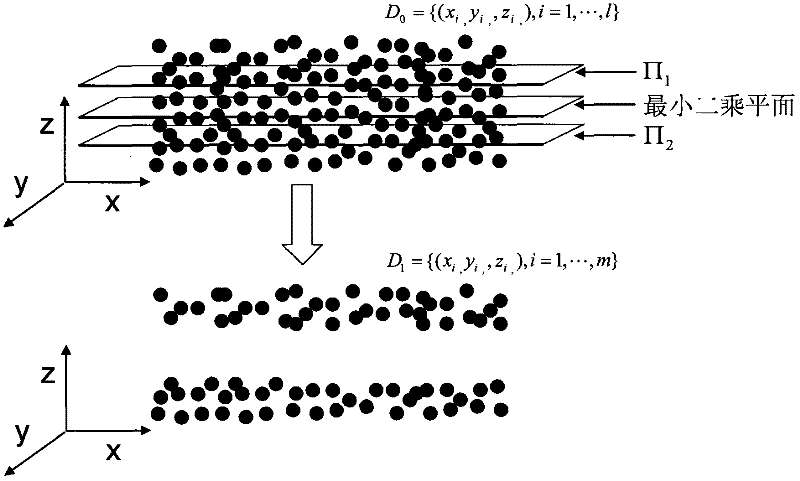
[0019] Step 20: Calculate the least squares plane corresponding to the measurement point set, and use the least squares plane as a reference to eliminate the measurement points with the smaller absolute value of the residual error.

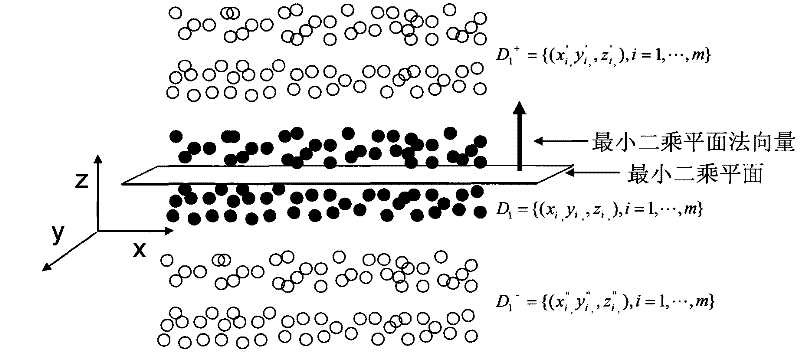
[0020] In step 30, the measurement points with large absolute values ​​are moved equally along the normal positive and negative directions of the least squares plane to form a linearly separable set of positive and negative...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

PUM

No PUM Login to view more

Abstract

The invention discloses a multi-measuring-point planeness evaluation method based on support vector classification. The method comprises the following steps: sampling points on a tested surface to obtain a three-dimensional coordinate measurement value of each point; calculating a least square surface corresponding to a measurement point set; with the least square surface as a reference, removing measurement points with a small residual absolute value; moving measurement points with a big residual absolute value for the same distance respectively along the positive direction and the negative direction of the normal direction of the least square surface to form a linearly separable positive point set and negative point set; calculating the maximum interval plane of the positive point set and the negative point set with a linearly classified support vector machine method; and calculating a planeness value according to the plane. According to the multiple-measuring-point planeness evaluation method, the calculation data amount in the multiple-measuring-point planeness evaluation can be reduced and the calculation efficiency and the accuracy of an evaluation result are obviously improved.

Description

technical field [0001] The invention relates to a flatness evaluation method, in particular to a multi-measurement point flatness evaluation method based on support vector classification. Background technique [0002] With the development of the national economy and the improvement of advanced manufacturing levels, in modern industrial manufacturing, especially in the fields of precision manufacturing, there are high precision requirements for the geometrical and dimensional accuracy of workpieces and structures. As one of the most common geometric dimensions of industrial products, planes are often used as pressure-bearing planes and reference planes in practical applications. If the flatness of the workpiece exceeds the design requirements, it will lead to uneven force on the pressure bearing surface, which will easily cause local deformation or damage of the pressure bearing surface, or cause the geometric dimensions of the components based on the plane to be out of align...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

Application Information

Patent Timeline
no application Login to view more
IPC IPC(8): G01B21/30
Inventor 刘桂雄姜焰鸣高屹
Owner SOUTH CHINA UNIV OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Try Eureka
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap