Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Approximation optimization and signal acquisition reconstruction method for 0-1 sparse cyclic matrix

A sparse circulant matrix and signal acquisition technology, applied in the field of compressed sensing, can solve the problem of low signal reconstruction ability of sparse circulant matrix, achieve the effects of improving signal reconstruction effect, simplifying hardware design and implementation, and wide application prospects

Active Publication Date: 2012-11-28
GUANGXI UNIVERSITY OF TECHNOLOGY
View PDF7 Cites 12 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0004] In order to solve the problems of low signal reconstruction capability of sparse circulant matrix and measurement matrix design, the present invention provides an approximate optimization and signal acquisition and reconstruction method of 0-1 sparse circulant matrix

Method used

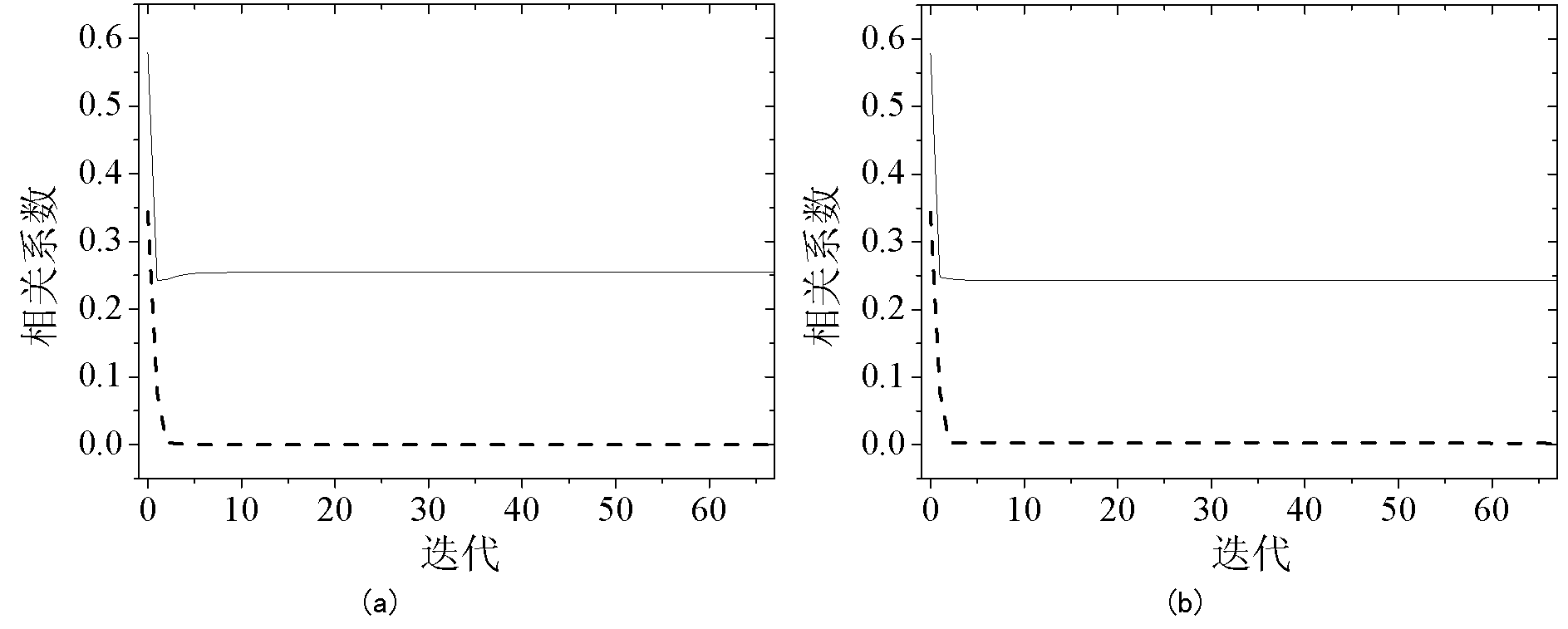
the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Approximation optimization and signal acquisition reconstruction method for 0-1 sparse cyclic matrix
  • Approximation optimization and signal acquisition reconstruction method for 0-1 sparse cyclic matrix
  • Approximation optimization and signal acquisition reconstruction method for 0-1 sparse cyclic matrix

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

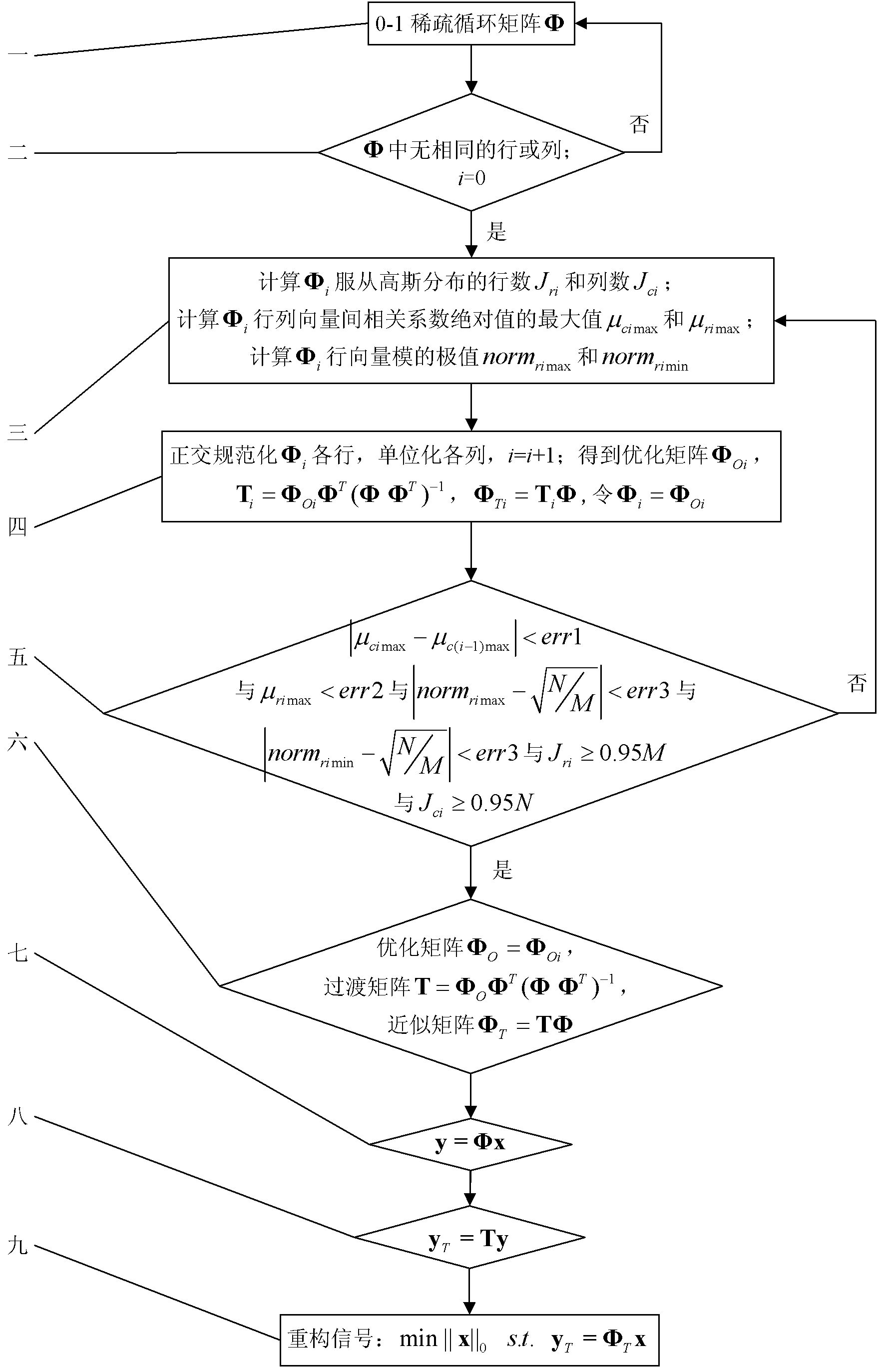
[0020] Specific implementation mode one: according to the instructions attached figure 1 This embodiment will be specifically described. A method for approximate optimization and signal acquisition and reconstruction of a 0-1 sparse circulant matrix, the process of the method is:

[0021] Step 1: Generate 0-1 sparse circular matrix , while making the optimization matrix ,in , . The initial row vector of is containing ( ) randomly distributed 0-1 sparse row vectors of 1, each row vector is the element of the previous row vector shifted to the right in turn ( and satisfied ) bit results. express The remainder operation of , , and are all natural numbers;

[0022] Step 2: Inspection Whether there is the same row or column in the same row or column, if it is, return to step 1, otherwise set the number of iterations i The initial value of 0, set the iteration error ;

[0023] Step 3: Calculation by Jarque-Bera test The number of rows that fol...

specific Embodiment approach 2

[0033] Specific embodiment 2: This specific embodiment is a further description of a Gaussian matrix optimization method based on compressed sensing described in specific embodiment 1. In step 2, the iterative error is set err 1 for , err 2 for , err 3 for .

specific Embodiment approach 3

[0034] Embodiment 3: This embodiment is a further description of the approximate optimization of a 0-1 sparse circulant matrix described in Embodiment 1 and the signal acquisition and reconstruction method. The orthogonal normalization described in step 4 Each row vector, and then the specific process of unitizing each column vector is: first Orthogonalize the row vectors, then normalize the row vectors, and finally normalize the column vectors.

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses an approximation optimization and signal acquisition reconstruction method for a 0-1 sparse cyclic matrix, belongs to the technical field for the design and optimization of measurement matrix in compressive sensing, and provides a posteriori optimizing method which is easy to implement by hardware and can ensure signal reconstruction effect, wherein the 0-1 sparse cyclic matrix is adopted in the measurement stage, and a Gaussian matrix is adopted in the reconstruction stage. The method comprises the following steps: orthonormalizing the row vector and unitizing the column vector of the measurement matrix obtained by the i-1th iteration by the ith iteration; and optimizing the 0-1 sparse cyclic matrix by taking the maximum value of the absolute value of the correlated coefficient between each row and column vector, the convergence stability of each row vector module and the row and column number of each row and column subjected to Gaussian distribution as the criteria. The posteriori optimization of the measured data and measured matrix is completed by solving a transition matrix and an approximate matrix. The method establishes the foundation for the compressive sensing to be practical from the theoretical study.

Description

technical field [0001] The invention belongs to the technical field of compressed sensing, and specifically provides an approximate optimization and signal acquisition and reconstruction method of a 0-1 sparse circulatory matrix. Background technique [0002] The design, optimization and properties of measurement matrices in compressed sensing are key factors for relational signal reconstruction. Although random matrices (Gaussian, Bernoulli and other matrices) have good signal reconstruction ability and universality, but due to the difficulty of hardware implementation, people turn to deterministic matrices with poor properties and easy hardware implementation (Toplitz, cycle, polynomial matrix, etc.). The circular matrix in the measurement matrix is ​​easy to implement in hardware, and can be quickly solved by discrete Fourier transform; the 0-1 sparse matrix is ​​not only easy to implement in hardware, but also requires a small storage space and has a fast operation ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): H03M7/30G06F17/15
Inventor 朱国宾程涛
Owner GUANGXI UNIVERSITY OF TECHNOLOGY
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com