Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Filtering backstepping ship movement control system based on self-adaption fuzzy estimator

A technology of self-adaptive fuzzy control system, applied in the direction of self-adaptive control, general control system, control/regulation system, etc., to achieve the effect of simple form, enhanced suppression ability, and improved robust performance

Active Publication Date: 2014-02-19
哈尔滨船海智能装备科技有限公司
View PDF2 Cites 12 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, the above studies are all carried out for systems with known models.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Filtering backstepping ship movement control system based on self-adaption fuzzy estimator
  • Filtering backstepping ship movement control system based on self-adaption fuzzy estimator
  • Filtering backstepping ship movement control system based on self-adaption fuzzy estimator

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

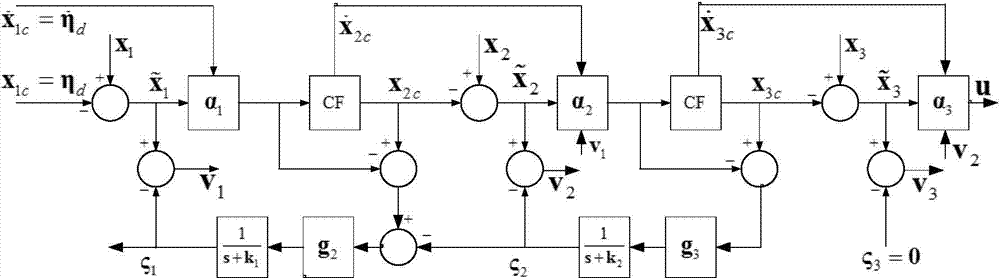
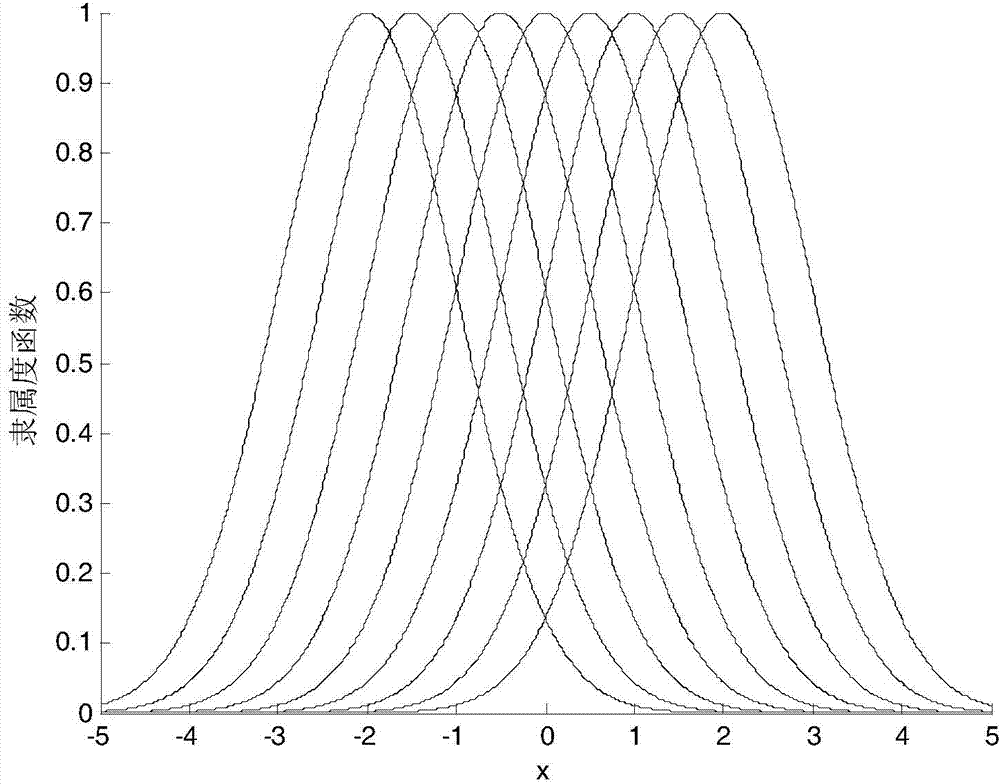
[0024] The present invention is described in detail below:

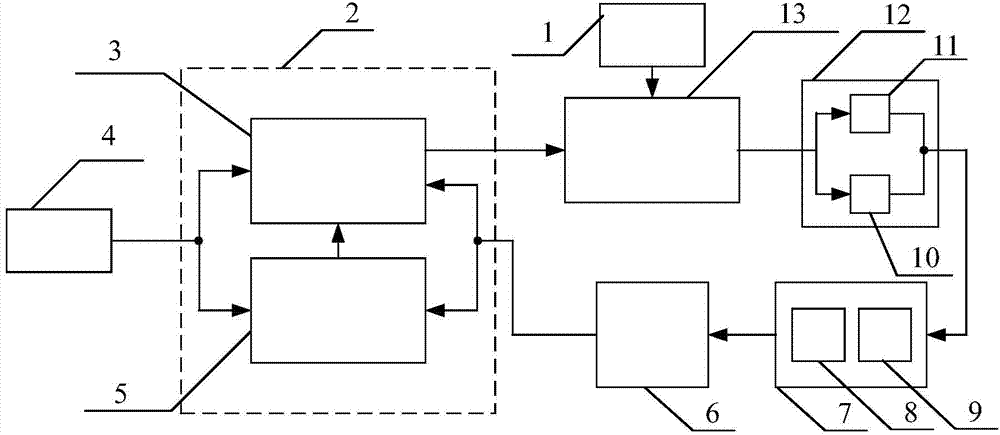
[0025] figure 1 The overall structure of the filter backstepping ship motion control system based on the adaptive fuzzy estimator of the present invention is given. figure 1 The meanings of the numbers in are as follows: 1—Environmental disturbance; 2—Control system; 3—Filter backstepping controller; 4—Guidance system; 5—Adaptive fuzzy estimator; 6—Diffeomorphic converter; 7— Data processing system; 8—filtering system; 9—data fusion system; 10—speed sensor; 11—position and attitude sensor; 12—sensor system; 13—ship.

[0026] combine figure 1 , The filtering backstepping ship motion control system based on the adaptive fuzzy estimator of the present invention includes a control system 2 , a guidance system 4 , a diffeomorphic converter 6 , a data processing system 7 , and a sensor system 12 . The pose sensor 11 in the sensor system 12 collects the actual pose of the ship, packs and transmits to the data processing ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides a filtering backstepping ship movement control system based on a self-adaption fuzzy estimator. The filtering backstepping ship movement control system comprises a control system (2), a guide system (4), a diffeomorphism exchanger (6), a data processing system (7) and a sensor system (12). The guide system (4) obtains the expectation position, the expectation heading and the expectation speed of a ship at each moment. The sensor system (12) comprises a pose sensor (11) and a speed sensor (10). The data processing system (7) comprises a data fusion system (9) and a filtering system (8). The control system (2) comprises a filtering backstepping controller (3) and the self-adaption fuzzy estimator (5). The self-adaption fuzzy estimator (5) simultaneously receives data from the guide system (4) and the diffeomorphism exchanger (6). The filtering backstepping controller (3) simultaneously receives expectation information and differential coefficients of the expectation information which are provided by the guide system (4), new state variable information provided by the diffeomorphism exchanger (6), and estimated output, provided by the self-adaption fuzzy estimator (5), for unknown nonlinear functions.

Description

technical field [0001] The invention relates to a ship motion control system. Background technique [0002] In recent years, rich marine resources have attracted the attention of all countries, and countries have also paid more and more attention to marine engineering and marine development. With the increasing frequency of people's sea activities, the fields related to ship control have attracted extensive attention of researchers. Ship course control, track control, path tracking and dynamic positioning technology have also become hot spots in the field of control research. [0003] In the design process of ship motion controllers, most nonlinear control methods are based on model information, and it is usually very difficult to establish an accurate system model, so the research on ship motion when the model has unknown information is based on adaptive fuzzy Estimator nonlinear control method is necessary. In addition, in the process of controller design using the conve...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G05B13/02
CPCG05D1/0206
Inventor 夏国清邵兴超栾添添杨月
Owner 哈尔滨船海智能装备科技有限公司
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com